Difference between revisions of "Exercise 2.13Z: Combination of BWT and MTF"
From LNTwww
| Line 3: | Line 3: | ||
[[File:EN_Inf_Z_2_14b.png|right|frame|Scheme for Burrows-Wheeler data compression]] | [[File:EN_Inf_Z_2_14b.png|right|frame|Scheme for Burrows-Wheeler data compression]] | ||
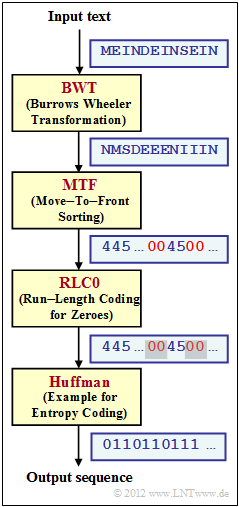
| − | We refer to the theory | + | We refer to the theory section [[Information_Theory/Weitere_Quellencodierverfahren#Application_scenario_for_the_Burrows-Wheeler_transformation|Application Scenario for the Burrows-Wheeler Transform]] and consider the coding system sketched on the right, consisting of the blocks |
* "Burrows–Wheeler Transform"</i> $\rm (BWT)$ as described in [[Aufgaben:2.13_Burrows-Wheeler-Rücktransformation|Exercise 2.13]]; the character sets at the input and the output of the BWT are the same: $\{$ $\rm D$, $\rm E$, $\rm I$, $\rm M$, $\rm N$, $\rm S$ $\}$; | * "Burrows–Wheeler Transform"</i> $\rm (BWT)$ as described in [[Aufgaben:2.13_Burrows-Wheeler-Rücktransformation|Exercise 2.13]]; the character sets at the input and the output of the BWT are the same: $\{$ $\rm D$, $\rm E$, $\rm I$, $\rm M$, $\rm N$, $\rm S$ $\}$; | ||
* "Move–to–Front" $\rm (MTF)$, a sorting algorithm that outputs a string of the same length $($ $N = 12$ in the example$)$, but with a different alphabet $\{$<b>0</b>, <b>1</b>, <b>2</b>, <b>3</b>, <b>4</b>, <b>5</b>$\}$; | * "Move–to–Front" $\rm (MTF)$, a sorting algorithm that outputs a string of the same length $($ $N = 12$ in the example$)$, but with a different alphabet $\{$<b>0</b>, <b>1</b>, <b>2</b>, <b>3</b>, <b>4</b>, <b>5</b>$\}$; | ||
| Line 26: | Line 26: | ||
<u>Hints:</u> | <u>Hints:</u> | ||
*The exercise belongs to the chapter [[Information_Theory/Further_Source_Coding_Methods|Further Source Coding Methods]]. | *The exercise belongs to the chapter [[Information_Theory/Further_Source_Coding_Methods|Further Source Coding Methods]]. | ||
| − | *In particular, reference is made to the | + | *In particular, reference is made to the section [[Information_Theory/Further_Source_Coding_Methods#Burrows.E2.80.93Wheeler_transformation|Burrows–Wheeler Transformation]]. |
*Information on the Huffman code can be found in the chapter [[Information_Theory/Entropiecodierung_nach_Huffman|Entropy Coding according to Huffman]]. This information is not necessary for the solution of the task. | *Information on the Huffman code can be found in the chapter [[Information_Theory/Entropiecodierung_nach_Huffman|Entropy Coding according to Huffman]]. This information is not necessary for the solution of the task. | ||
| Line 73: | Line 73: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
[[File:EN_Inf_Z_2_14.png|right|frame|Example of the MTF algorithm]] | [[File:EN_Inf_Z_2_14.png|right|frame|Example of the MTF algorithm]] | ||
| − | '''(1)''' The graph on the information | + | '''(1)''' The graph on the information section shows that <u>solution suggestions 1 and 2</u> are correct and suggestion 3 is incorrect: |
*$\rm E$ and $\rm I$ occur grouped together, | *$\rm E$ and $\rm I$ occur grouped together, | ||
*but not the $\rm N$ characters. | *but not the $\rm N$ characters. | ||
Latest revision as of 00:05, 13 November 2022
We refer to the theory section Application Scenario for the Burrows-Wheeler Transform and consider the coding system sketched on the right, consisting of the blocks
- "Burrows–Wheeler Transform" $\rm (BWT)$ as described in Exercise 2.13; the character sets at the input and the output of the BWT are the same: $\{$ $\rm D$, $\rm E$, $\rm I$, $\rm M$, $\rm N$, $\rm S$ $\}$;
- "Move–to–Front" $\rm (MTF)$, a sorting algorithm that outputs a string of the same length $($ $N = 12$ in the example$)$, but with a different alphabet $\{$0, 1, 2, 3, 4, 5$\}$;
- $\rm RLC0$ – a run-length encoding specifically for 0, which is (as) frequent according to $\rm BWT$ and $\rm MTF$; all other indices are not changed by $\rm RLC0$ ;
- $\rm Huffman$ as described in the chapter Entropy coding according to Huffman; frequent characters are represented by short binary sequences and rare ones by long ones.
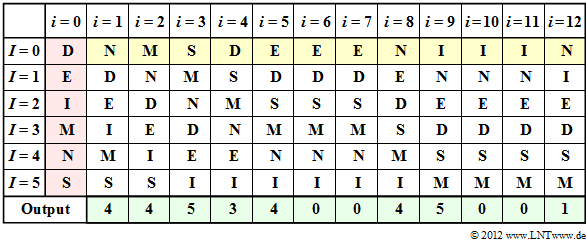
The $\rm MTF$ algorithm can be described as follows for $M = 6$ input symbols:
- The output sequence of the $\rm MTF$ is a string of indices from the set
- $ I = \{$0, 1, 2, 3, 4, 5$\}$.
- Before starting the actual $\rm MTF$ algorithm, the possible input symbols are sorted lexicographically and assigned to the following indices:
- $\rm D$ → 0, $\rm E$ → 1, $\rm I$ → 2, $\rm M$ → 3, $\rm N$ → 4, $\rm S$ → 5.
- Let the $\rm MTF$ input string here be $\rm N\hspace{0.05cm}M\hspace{0.05cm}S\hspace{0.05cm}D\hspace{0.05cm}E\hspace{0.05cm}E\hspace{0.05cm}E\hspace{0.05cm}N\hspace{0.05cm}I\hspace{0.05cm}I\hspace{0.05cm}I\hspace{0.05cm}N$. This was the $\rm BWT$ result in Exercise 2.13. The first $\rm N$ is represented as $I = 4$ according to the default setting.
- Then the $\rm N$ is placed at the beginning in the sorting, so that after the coding step $i = 1$ the assignment holds:
- $\rm N$ → 0, $\rm D$ → 1, $\rm E$ → 2, $\rm I$ → 3, $\rm M$ → 4, $\rm S$ → 5.
- Continue in the same way until the entire input text has been processed. If a character is already at position 0, no reordering is necessary.
Hints:
- The exercise belongs to the chapter Further Source Coding Methods.
- In particular, reference is made to the section Burrows–Wheeler Transformation.
- Information on the Huffman code can be found in the chapter Entropy Coding according to Huffman. This information is not necessary for the solution of the task.
Questions
Solution
(1) The graph on the information section shows that solution suggestions 1 and 2 are correct and suggestion 3 is incorrect:
- $\rm E$ and $\rm I$ occur grouped together,
- but not the $\rm N$ characters.
(2) Proposed solutions 2 and 3 are correct:
- The input sequence is processed "character by character".
Thus, the output sequence also has the length $N = 12$. - In fact, the input set $\{ \hspace{0.05cm}\rm D,\hspace{0.05cm} E,\hspace{0.05cm} I,\hspace{0.05cm} M,\hspace{0.05cm} N , \hspace{0.05cm} S \}$ is converted into the output set $\{ \hspace{0.05cm}\rm 0,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 3,\hspace{0.05cm} 4 , \hspace{0.05cm} 5 \}$.
- However, not by simple "mapping", but by an algorithm which is outlined below.
(3) Correct is solution suggestion 2:
- The table shows the MTF algorithm. The step $i=0$ (red background) indicates the preassignment. The MTF input is highlighted in yellow, the output in green.
- In step $i=1$, the input character $\rm N$ corresponding to column $i=0$ is represented by index $I = 4$ . Subsequently, $\rm N$ is sorted to the front, while the order of the other characters remains the same.
- The input character $\rm M$ in the second step is also given the index $I = 4$ according to column $i=2$ . One continues in the same way until the twelfth character $\rm N$, to which the index $I = 1$ is assigned.
- You can see from the above table that at the times $i=6$, $i=7$, $i=10$ and $i=11$ the output index is $I = 0$ .
(4) Statements 1 and 2 are correct:
- The preprocessings "BWT" and "MTF" only have the task to generate as many zeros as possible.
(5) All statements are correct.
- You can find more information on the Huffman algorithm in the chapter "Entropy coding according to Huffman".