Difference between revisions of "Aufgaben:Exercise 3.10Z: Maximum Likelihood Decoding of Convolutional Codes"
From LNTwww
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Convolutional_Codes}} | {{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Convolutional_Codes}} | ||
| − | [[File: | + | [[File:EN_KC_Z_3_10.png|right|frame|Overall system model, given for this exercise]] |
The Viterbi algorithm represents the best known realization form for the maximum likelihood decoding of a convolutional code. We assume here the following model: | The Viterbi algorithm represents the best known realization form for the maximum likelihood decoding of a convolutional code. We assume here the following model: | ||
* The information sequence $\underline{u}$ is converted into the code sequence $\underline{x}$ by a convolutional code. | * The information sequence $\underline{u}$ is converted into the code sequence $\underline{x}$ by a convolutional code. | ||
| Line 7: | Line 7: | ||
*It is valid $u_i ∈ \{0, \, 1\}$. In contrast, the code symbols are represented bipolar ⇒ $x_i ∈ \{–1, \, +1\}$. | *It is valid $u_i ∈ \{0, \, 1\}$. In contrast, the code symbols are represented bipolar ⇒ $x_i ∈ \{–1, \, +1\}$. | ||
| − | * Let the channel be given by the models [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{BSC}$]] ⇒ received values $y_i ∈ \{–1, \, +1\}$ or [[Channel_Coding/Channel_Models_and_Decision_Structures# | + | * Let the channel be given by the models [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|$\text{BSC}$]] ⇒ received values $y_i ∈ \{–1, \, +1\}$ or [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input| $\text{AWGN}$]] ⇒ $y_i$ real-valued. |
* Given a received sequence $\underline{y}$ the Viterbi algorithm decides for the sequence $\underline{z}$ according to | * Given a received sequence $\underline{y}$ the Viterbi algorithm decides for the sequence $\underline{z}$ according to | ||
| Line 44: | Line 44: | ||
* For more information on this topic, see the following sections in this book: | * For more information on this topic, see the following sections in this book: | ||
| − | + | :* [[Channel_Coding/Channel_Models_and_Decision_Structures#Criteria_.C2.BBMaximum-a-posteriori.C2.AB_and_.C2.BBMaximum-Likelihood.C2.AB| "MAP and ML criterion"]], | |
| − | + | :* [[Channel_Coding/Channel_Models_and_Decision_Structures#Maximum-likelihood_decision_at_the_BSC_channel| "ML decision at the BSC channel"]], | |
| − | + | :* [[Channel_Coding/Channel_Models_and_Decision_Structures#Maximum-likelihood_decision_at_the_AWGN_channel| "ML decision at the AWGN channel"]], | |
| − | + | :* [[Channel_Coding/Decoding_of_Linear_Block_Codes#Block_diagram_and_requirements| "Decoding linear block codes"]]. | |
| Line 58: | Line 58: | ||
{How are $d_{\rm H}(\underline{x}, \, \underline{y})$ and $d_{\rm E}(\underline{x}, \, \underline{y})$ related in the BSC model? | {How are $d_{\rm H}(\underline{x}, \, \underline{y})$ and $d_{\rm E}(\underline{x}, \, \underline{y})$ related in the BSC model? | ||
|type="()"} | |type="()"} | ||
| − | - $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}(\underline{x}, \, \underline{y})$ is valid. | + | - $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}(\underline{x}, \, \underline{y})$ is valid. |
| − | - $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}^2(\underline{x}, \, \underline{y})$ is valid. | + | - $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}^2(\underline{x}, \, \underline{y})$ is valid. |
| − | + $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}^2(\underline{x}, \, \underline{y})/4$ is valid. | + | + $d_{\rm H}(\underline{x}, \, \underline{y}) = d_{\rm E}^2(\underline{x}, \, \underline{y})/4$ is valid. |
{Which of the equations describe the maximum likelihood decoding in the BSC model? The minimization/maximization refers alwaysto all $\underline{x} ∈\mathcal{ C}$. | {Which of the equations describe the maximum likelihood decoding in the BSC model? The minimization/maximization refers alwaysto all $\underline{x} ∈\mathcal{ C}$. | ||
| Line 82: | Line 82: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct is the <u>proposed solution 3</u>: | + | '''(1)''' Correct is the <u>proposed solution 3</u>: |
| − | *Let the two binary sequences be $\underline{x}$ and $\underline{y}$ with $x_i ∈ \{-1, \, +1\}, \ y_i ∈ \{-1, \, +1\}$. Let the sequence length be $L$ in each case. | + | *Let the two binary sequences be $\underline{x}$ and $\underline{y}$ with $x_i ∈ \{-1, \, +1\}, \ y_i ∈ \{-1, \, +1\}$. Let the sequence length be $L$ in each case. |
| − | *The Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$ gives the number of bits in which $\underline{x}$ and $\underline{y}$ differ, for which thus $x_i \, - y_i = ±2$ ⇒ $ (x_i \, - y_i)^2 = 4$ holds. | + | |
| − | *Equal symbols $(x_i = y_i)$ do not contribute to the Hamming | + | *The Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$ gives the number of bits in which $\underline{x}$ and $\underline{y}$ differ, for which thus $x_i \, - y_i = ±2$ ⇒ $ (x_i \, - y_i)^2 = 4$ holds. |
| + | |||
| + | *Equal symbols $(x_i = y_i)$ do not contribute to the Hamming distance and give $(x_i \, – y_i)^2 = 0$. According to the <u>solution 3</u>, we can therefore write: | ||
:$$ d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = | :$$ d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = | ||
\frac{1}{4} \cdot \sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2= \frac{1}{4} \cdot d_{\rm E}^2(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$ | \frac{1}{4} \cdot \sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2= \frac{1}{4} \cdot d_{\rm E}^2(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$ | ||
| − | '''(2)''' <u>All proposed solutions</u> are correct: | + | '''(2)''' <u>All proposed solutions</u> are correct: |
| − | *In the BSC model, it is common practice to select the code word $\underline{x}$ with the smallest Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$ for the given received vector $\underline{y}$: | + | *In the BSC model, it is common practice to select the code word $\underline{x}$ with the smallest Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$ for the given received vector $\underline{y}$: |
:$$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | :$$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$ | d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$ | ||
| − | *But according to the subtask '''(1)''' also applies: | + | *But according to the subtask '''(1)''' also applies: |
:$$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | :$$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} | ||
d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})/4 | d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})/4 | ||
| Line 103: | Line 105: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The factor $1/4$ does not matter for the minimization. Since $d_{\rm E}(\underline{x}, \, \underline{y}) ≥ 0$, it does not matter whether the minimization is done with respect to $d_{\rm E}(\underline{x}, \, \underline{y})$ or $d_{\rm E}^2(\underline{x}, \, \underline{y})$. | + | *The factor $1/4$ does not matter for the minimization. Since $d_{\rm E}(\underline{x}, \, \underline{y}) ≥ 0$, it does not matter whether the minimization is done with respect to $d_{\rm E}(\underline{x}, \, \underline{y})$ or $d_{\rm E}^2(\underline{x}, \, \underline{y})$. |
| − | '''(3)''' Correct is the <u>proposed solution 2</u>: | + | '''(3)''' Correct is the <u>proposed solution 2</u>: |
*The square of the Euclidean distance can be expressed as follows: | *The square of the Euclidean distance can be expressed as follows: | ||
:$$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = | :$$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = | ||
| Line 115: | Line 117: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The first two summands are each equal to $L$ and need not be considered for minimization. | + | *The first two summands are each equal to $L$ and need not be considered for minimization. |
| − | *For the last expression in this equation, $–2 \cdot 〈 \underline{x}, \, \underline{y} 〉$ can be written. | + | |
| − | *Due to the negative sign, minimization becomes maximization ⇒ <u>answer 2</u>. | + | *For the last expression in this equation, $–2 \cdot 〈 \underline{x}, \, \underline{y} 〉$ can be written. |
| + | |||
| + | *Due to the negative sign, minimization becomes maximization ⇒ <u>answer 2</u>. | ||
| − | '''(4)''' Correct are <u>proposed solutions 2 and 3</u>: | + | '''(4)''' Correct are the <u>proposed solutions 2 and 3</u>: |
| − | *For the AWGN channel, unlike the BSC, no Hamming distance can be specified. | + | *For the AWGN channel, unlike the BSC, no Hamming distance can be specified. |
| + | |||
*Based on the equation | *Based on the equation | ||
:$$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = | :$$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = | ||
| Line 128: | Line 133: | ||
\hspace{0.1cm}-2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot y_i$$ | \hspace{0.1cm}-2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot y_i$$ | ||
| − | :the same statements apply for the first and last summands as for the BSC model – see subtask (3). | + | :the same statements apply for the first and last summands as for the BSC model – see subtask '''(3)'''. |
| − | *For the middle summand, $y_i = x_i + n_i$ and $x_i ∈ \{–1, \, +1\}$ hold: | + | |
| + | *For the middle summand, $y_i = x_i + n_i$ and $x_i ∈ \{–1, \, +1\}$ hold: | ||
:$$\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} = | :$$\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} = | ||
\hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} n_i^{\hspace{0.15cm}2} | \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} n_i^{\hspace{0.15cm}2} | ||
\hspace{0.1cm}+2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot n_i \hspace{0.05cm}.$$ | \hspace{0.1cm}+2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot n_i \hspace{0.05cm}.$$ | ||
| − | *The first summand again | + | *The first summand gives again $L$, the second is proportional to the noise power, and the last term vanishes since $\underline{x}$ and $\underline{n}$ are uncorrelated. |
| − | *So for minimizing $d_{\rm E}(\underline{x}, \, \underline{y})$, the sum over $y_i^2$ need not be considered since there is no relation to the code sequences $\underline{x}$. | + | |
| + | *So for minimizing $d_{\rm E}(\underline{x}, \, \underline{y})$, the sum over $y_i^2$ need not be considered since there is no relation to the code sequences $\underline{x}$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 15:57, 21 November 2022
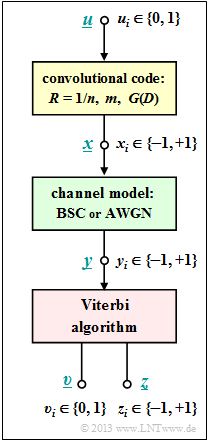
The Viterbi algorithm represents the best known realization form for the maximum likelihood decoding of a convolutional code. We assume here the following model:
- The information sequence $\underline{u}$ is converted into the code sequence $\underline{x}$ by a convolutional code.
- It is valid $u_i ∈ \{0, \, 1\}$. In contrast, the code symbols are represented bipolar ⇒ $x_i ∈ \{–1, \, +1\}$.
- Let the channel be given by the models $\text{BSC}$ ⇒ received values $y_i ∈ \{–1, \, +1\}$ or $\text{AWGN}$ ⇒ $y_i$ real-valued.
- Given a received sequence $\underline{y}$ the Viterbi algorithm decides for the sequence $\underline{z}$ according to
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$$
- This corresponds to the "Maximum a posteriori" $\rm (MAP)$ criterion. If all information sequences $\underline{u}$ are equally likely, this transitions to the somewhat simpler "Maximum likelihood criterion" $\rm (ML)$:
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{y} \hspace{0.05cm}|\hspace{0.05cm} \underline{x}_{\hspace{0.03cm}i} ) \hspace{0.05cm}.$$
- As a further result, the Viterbi algorithm additionally outputs the sequence $\underline{v}$ as an estimate for the information sequence $\underline{u}$.
In this exercise, you should determinethe relationship between the $\text{Hamming distance}$ $d_{\rm H}(\underline{x}, \, \underline{y})$ and the $\text{Euclidean distance}$
- $$d_{\rm E}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \sqrt{\sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2}\hspace{0.05cm}.$$
Then, the above maximum likelihood criterion is to be formulated with
- the Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$,
- the Euclidean distance $d_{\rm E}(\underline{x}, \, \underline{y})$, and
- the $\text{correlation value}$ $〈 x \cdot y 〉$.
Hints:
- This exercise refers to the chapter "Decoding of Convolutional Codes".
- Reference is made in particular to the section "Viterbi algorithm – based on correlation and metrics".
- For simplicity, "tilde" and "apostrophe" are omitted.
- For more information on this topic, see the following sections in this book:
Questions
Solution
(1) Correct is the proposed solution 3:
- Let the two binary sequences be $\underline{x}$ and $\underline{y}$ with $x_i ∈ \{-1, \, +1\}, \ y_i ∈ \{-1, \, +1\}$. Let the sequence length be $L$ in each case.
- The Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$ gives the number of bits in which $\underline{x}$ and $\underline{y}$ differ, for which thus $x_i \, - y_i = ±2$ ⇒ $ (x_i \, - y_i)^2 = 4$ holds.
- Equal symbols $(x_i = y_i)$ do not contribute to the Hamming distance and give $(x_i \, – y_i)^2 = 0$. According to the solution 3, we can therefore write:
- $$ d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \frac{1}{4} \cdot \sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2= \frac{1}{4} \cdot d_{\rm E}^2(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$
(2) All proposed solutions are correct:
- In the BSC model, it is common practice to select the code word $\underline{x}$ with the smallest Hamming distance $d_{\rm H}(\underline{x}, \, \underline{y})$ for the given received vector $\underline{y}$:
- $$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})\hspace{0.05cm}.$$
- But according to the subtask (1) also applies:
- $$\underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y})/4 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \underline{z} = {\rm arg} \min_{\underline{x} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm E}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) \hspace{0.05cm}.$$
- The factor $1/4$ does not matter for the minimization. Since $d_{\rm E}(\underline{x}, \, \underline{y}) ≥ 0$, it does not matter whether the minimization is done with respect to $d_{\rm E}(\underline{x}, \, \underline{y})$ or $d_{\rm E}^2(\underline{x}, \, \underline{y})$.
(3) Correct is the proposed solution 2:
- The square of the Euclidean distance can be expressed as follows:
- $$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \sum_{i=1}^{L} \hspace{0.2cm}(x_i - y_i)^2 = \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} \hspace{0.1cm}-2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot y_i \hspace{0.05cm}.$$
- The first two summands are each equal to $L$ and need not be considered for minimization.
- For the last expression in this equation, $–2 \cdot 〈 \underline{x}, \, \underline{y} 〉$ can be written.
- Due to the negative sign, minimization becomes maximization ⇒ answer 2.
(4) Correct are the proposed solutions 2 and 3:
- For the AWGN channel, unlike the BSC, no Hamming distance can be specified.
- Based on the equation
- $$d_{\rm E}^{\hspace{0.15cm}2}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{y}) = \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} \hspace{0.1cm}-2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot y_i$$
- the same statements apply for the first and last summands as for the BSC model – see subtask (3).
- For the middle summand, $y_i = x_i + n_i$ and $x_i ∈ \{–1, \, +1\}$ hold:
- $$\sum_{i=1}^{L} \hspace{0.1cm} y_i^{\hspace{0.15cm}2} = \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} x_i^{\hspace{0.15cm}2} \hspace{0.1cm}+ \hspace{0.1cm}\sum_{i=1}^{L} \hspace{0.1cm} n_i^{\hspace{0.15cm}2} \hspace{0.1cm}+2 \cdot \sum_{i=1}^{L} \hspace{0.1cm} x_i \cdot n_i \hspace{0.05cm}.$$
- The first summand gives again $L$, the second is proportional to the noise power, and the last term vanishes since $\underline{x}$ and $\underline{n}$ are uncorrelated.
- So for minimizing $d_{\rm E}(\underline{x}, \, \underline{y})$, the sum over $y_i^2$ need not be considered since there is no relation to the code sequences $\underline{x}$.