Difference between revisions of "Channel Coding/General Description of Linear Block Codes"
| (53 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Binary Block Codes for Channel Coding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Examples of Binary Block Codes |
| − | |Nächste Seite= | + | |Nächste Seite=Decoding of Linear Block Codes |
}} | }} | ||
| − | == | + | == Linear codes and cyclic codes == |
<br> | <br> | ||
| − | + | All codes mentioned so far are »'''linear'''«: | |
| − | * | + | *the [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes|$\text{single parity-check code}$]] $\rm (SPC)$, |
| − | + | ||
| − | * | + | *the [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|$\text{repetition code}$]] $\rm (RC)$, |
| − | + | *the [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|$\text{Hamming code}$]] $\rm (HC)$. | |
| + | |||
| + | |||
| + | Now the definition of "linearity" valid for binary block codes is added.<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A »'''linear binary block code'''« $\mathcal{C}$ is a set of $2^k$ code words $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$, where the (modulo 2) sum of any two code words $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ again gives a valid code word: |
::<math>\underline{x}, \underline{x}\hspace{0.05cm}' \in {\rm GF}(2^n),\hspace{0.3cm} \underline{x}, \underline{x}\hspace{0.05cm}' \in \mathcal{C} | ::<math>\underline{x}, \underline{x}\hspace{0.05cm}' \in {\rm GF}(2^n),\hspace{0.3cm} \underline{x}, \underline{x}\hspace{0.05cm}' \in \mathcal{C} | ||
| Line 22: | Line 25: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *This condition must also be satisfied for $\underline{x} = \underline{x}\hspace{0.05cm}'$ .<br> | |
| − | + | *For the remainder of this book, modulo addition will no longer be expressed by the "modulo sign" to simplify notation, but by the conventional "plus sign".}} <br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We consider two $\text{(3, 2)}$ block codes: |
::<math>\mathcal{C}_1 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 0, 1) \hspace{0.05cm},(1, 1, 0) \}\hspace{0.05cm},</math> | ::<math>\mathcal{C}_1 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 0, 1) \hspace{0.05cm},(1, 1, 0) \}\hspace{0.05cm},</math> | ||
| Line 33: | Line 36: | ||
::<math>\mathcal{C}_2 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 1, 0) \hspace{0.05cm},(1, 1, 1) \hspace{0.05cm}.</math> | ::<math>\mathcal{C}_2 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 1, 0) \hspace{0.05cm},(1, 1, 1) \hspace{0.05cm}.</math> | ||
| − | + | You can see: | |
| − | * | + | *The code $\mathcal{C}_1$ is linear, since the modulo 2 addition of any two code words always yields also a valid code word, e.g. $(0, 1, 1) + (1, 0, 1) = (1, 1, 0)$.<br> |
| + | |||
| + | *The above definition also applies to the modulo 2 addition of a code word with itself, e.g. $(0, 1, 1) + (0, 1, 1) = (0, 0, 0)$. | ||
| − | * | + | *From this follows: Each linear code contains the all-zero word $\underline{0}$.<br> |
| − | * | + | *Although the last condition is satisfied, $\mathcal{C}_2$ is not a linear code. Indeed, for this code: $(0, 1, 1) + (1, 1, 0) = (1, 0, 1)$. This is not a valid code word of $\mathcal{C}_2$.}}<br> |
| − | + | In the following, we restrict ourselves exclusively to linear codes, since non-linear codes are of secondary importance for practical use.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A linear block code $\mathcal{C}$ is called »'''cyclic'''« if every cyclic shift of a code word $\underline{x}$ $($to the left or right$)$ results in a valid code word: |
| − | ::<math>\underline{x}= (x_1, x_2, ... \hspace{0.05cm}, x_n) \in \mathcal{C} | + | ::<math>\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) \in \mathcal{C} |
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x}\hspace{0.05cm}'= (x_n, x_1, ... \hspace{0.05cm}, x_{n-1}) \in \mathcal{C} | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x}\hspace{0.05cm}'= (x_n, x_1, \hspace{0.05cm}\text{...} \hspace{0.05cm} \hspace{0.05cm}, x_{n-1}) \in \mathcal{C} |
\hspace{0.05cm}.</math>}}<br> | \hspace{0.05cm}.</math>}}<br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {{GraueBox|TEXT= |
| + | [[File:P ID2354 KC T 1 3 S3c.png|right|frame|Code table of the systematic $\text{(7, 4, 3)}$ Hamming code;<br> | ||
| + | black: $k= 4$ information bits, red: $n-k = 3$ parity bits ]] | ||
| + | $\text{Example 2:}$ You can see from the table for the [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|$\text{HC (7, 4, 3)}$]] that it is linear and cyclic. | ||
| + | <br><br><br> | ||
| + | *A valid code word results even if all bits are inverted: $0 ↔ 1$. | ||
| + | |||
| + | *Also the $\underline{0}$ word $(n$ times a "zero"$)$ and the $\underline{1}$ word $(n$ times a "one"$)$ are allowed with this code.}}<br> | ||
| + | |||
| + | == Code definition by the parity-check matrix == | ||
<br> | <br> | ||
| − | [[File:P ID2355 KC T 1 3 S3.png|right|frame|(7, 4, 3) | + | [[File:P ID2355 KC T 1 3 S3.png|right|frame|Chart for the $\text{(7, 4, 3)}$ Hamming code]] |
| − | + | We consider the [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|$\text{(7, 4, 3)}$ Hamming code]] with code words $\underline{x}$ of length $n=7$, consisting of | |
| − | * | + | *$k = 4$ information bits $x_1$, $x_2$, $x_3$, $x_4$, and<br> |
| − | |||
| − | + | *$m = n-k = 3$ parity bits $x_5$, $x_6$, $x_7$.<br><br> | |
| − | : | + | The parity-check equations are (see graphic on the right): |
| − | |||
| − | |||
| − | In | + | ::<math>x_1 + x_2 + x_3 + x_5 = 0 \hspace{0.05cm},</math> |
| + | ::<math>x_2 + x_3 + x_4 + x_6 = 0 \hspace{0.05cm},</math> | ||
| + | ::<math>x_1 + x_2 + x_4 + x_7 = 0 \hspace{0.05cm}. </math> | ||
| + | |||
| + | In matrix notation, this set of equations reads: | ||
::<math>{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} | ::<math>{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} | ||
\hspace{0.05cm}. </math> | \hspace{0.05cm}. </math> | ||
| − | In | + | In this equation are used: |
| − | * | + | *the »'''parity-check matrix'''« ${ \boldsymbol{\rm H}}$ with $m = n-k = 3$ rows and $n = 7$ columns: |
::<math>{ \boldsymbol{\rm H}} = \begin{pmatrix} | ::<math>{ \boldsymbol{\rm H}} = \begin{pmatrix} | ||
| Line 84: | Line 92: | ||
\end{pmatrix}\hspace{0.05cm},</math> | \end{pmatrix}\hspace{0.05cm},</math> | ||
| − | * | + | *the code word $\underline{x}= (x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm},\ x_7)$ of length $n = 7$,<br> |
| − | * | + | *the all-zero vector $\underline{0} = (0,\ 0,\ 0)$ of length $m = 3$.<br><br> |
| − | + | By "transposing", the row vectors $\underline{x}$ and $\underline{0}$ become the corresponding column vectors $\underline{x}^{\rm T}$ and $\underline{0}^{\rm T}$.<br> | |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ The graph illustrates the $m = 3$ parity-check equations of a code $\mathcal{C}$ with code parameters $n = 6$ and $k = 3$ in the order red, green and blue. Thus, $\mathcal{C}$ is not a Hamming code $(n \ne 2^m-1)$. |
| + | [[File:P ID2356 KC T 1 4 S2.png|right|frame|Chart for the $\text{(6, 3, 3)}$ block code]] | ||
| − | + | According to the equation $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T}$ the parity-check matrix is: | |
::<math> \boldsymbol{\rm H} = \begin{pmatrix} | ::<math> \boldsymbol{\rm H} = \begin{pmatrix} | ||
1 &1 &0 &1 &0 & 0\\ | 1 &1 &0 &1 &0 & 0\\ | ||
| Line 101: | Line 109: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | The $2^k = 8$ code words in systematic realization are (with the parity bits to the right of the small arrow): | |
| − | :<math>\underline{x}_0 = (0, 0, 0_{\hspace{0.01cm} \rightarrow} 0, 0, 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_1 = (0, 0, 1_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm},\hspace{0.5cm} | + | :<math>\underline{x}_0 = (0,\ 0,\ 0_{\hspace{0.01cm} \rightarrow} 0,\ 0,\ 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_1 = (0,\ 0,\ 1_{\hspace{0.01cm} \rightarrow}0,\ 1,\ 1)\hspace{0.05cm},\hspace{0.5cm} |
| − | \underline{x}_2 = (0, 1, 0_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\hspace{0.5cm}\underline{x}_3 = (0, 1, 1_{\hspace{0.01cm} \rightarrow}1, 1, 0)\hspace{0.05cm}, </math> | + | \underline{x}_2 = (0,\ 1,\ 0_{\hspace{0.01cm} \rightarrow}1,\ 0,\ 1)\hspace{0.05cm},\hspace{0.5cm}\underline{x}_3 = (0, 1, 1_{\hspace{0.01cm} \rightarrow}1,\ 1,\ 0)\hspace{0.05cm}, </math> |
| − | :<math>\underline{x}_4 = (1, 0, 0_{\hspace{0.01cm} \rightarrow} 1, 1, 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_5 = (1, 0, 1_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\hspace{0.5cm} | + | :<math>\underline{x}_4 = (1,\ 0,\ 0_{\hspace{0.01cm} \rightarrow} 1,\ 1,\ 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_5 = (1,\ 0,\ 1_{\hspace{0.01cm} \rightarrow}1,\ 0,\ 1)\hspace{0.05cm},\hspace{0.5cm} |
| − | \underline{x}_6 = (1, 1, 0_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm}, \hspace{0. | + | \underline{x}_6 = (1,\ 1,\ 0_{\hspace{0.01cm} \rightarrow}0,\ 1,\ 1)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_7 = (1,\ 1,\ 1_{\hspace{0.01cm} \rightarrow}0,\ 0,\ 0)\hspace{0.05cm}.</math> |
| − | + | It can be seen from these specifications: | |
| − | * | + | *The number of columns $\boldsymbol{\rm H}$ is equal to the code length $n$.<br> |
| − | * | + | *The number of lines of $\boldsymbol{\rm H}$ is equal to the number $m = n-k$ of parity-check equations.<br> |
| − | * | + | *From $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} $ it therefore does not follow that all code words contain an even number of ones.}}<br> |
| − | == | + | == Code definition by the generator matrix == |
<br> | <br> | ||
| − | + | The check matrix $\boldsymbol{\rm H}$ of a $(n, k)$ block code has | |
| + | *$n$ columns, | ||
| + | *$m = n-k$ rows. | ||
| + | |||
| + | |||
| + | However, the same code can be described by the matrix $\boldsymbol{\rm G}$ with | ||
| + | *also $n$ columns, | ||
| + | *but $k$ rows.<br> | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A linear binary block code $\mathcal{C}$ can be characterized by the »'''check matrix'''« $\boldsymbol{\rm H}$ or with the »'''generator matrix'''« $\boldsymbol{\rm G}$ as follows: |
::<math>\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\text{:} \hspace{0.2cm}{ \boldsymbol{\rm H} } \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \}\hspace{0.05cm},</math> | ::<math>\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\text{:} \hspace{0.2cm}{ \boldsymbol{\rm H} } \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \}\hspace{0.05cm},</math> | ||
| Line 126: | Line 142: | ||
\hspace{0.2cm}\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G} } \}\hspace{0.05cm}.</math>}}<br> | \hspace{0.2cm}\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G} } \}\hspace{0.05cm}.</math>}}<br> | ||
| − | + | Before we turn to the properties of the generator matrix, we describe the generation of the code words with an example.<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ We consider a linear $(5, 3)$ block code with the generator matrix (again: this is not a Hamming code!) |
| − | :<math> \boldsymbol{\rm G} = \begin{pmatrix} | + | ::<math> \boldsymbol{\rm G} = \begin{pmatrix} |
1 &1 &0 &1 &1\\ | 1 &1 &0 &1 &1\\ | ||
0 &1 &0 &1 &0\\ | 0 &1 &0 &1 &0\\ | ||
| Line 144: | Line 160: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *Thus, the information words $\underline{u}= (u_1,\ u_2,\ u_3)$ are assigned to the code words $\underline{x}= (x_1,\ x_2,\ x_3,\ x_4,\ x_5)$ according to the following equations. | |
| + | *The following always applies: $\underline{x} = \underline{u} \cdot \boldsymbol{\rm G}$: | ||
::<math>\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},</math> | ::<math>\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},</math> | ||
| Line 155: | Line 172: | ||
::<math>\underline{u}_7 =(1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+ \underline{g}_2+\underline{g}_3\hspace{0.05cm}.</math>}}<br> | ::<math>\underline{u}_7 =(1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+ \underline{g}_2+\underline{g}_3\hspace{0.05cm}.</math>}}<br> | ||
| − | + | Notes: | |
| − | * | + | *The basis vectors used here for the calculation $\underline{g}_1$, $\underline{g}_2$ and $\underline{g}_3$ – each with length $n = 5$ – correspond to the $k = 3$ rows of the generator matrix $\boldsymbol{\rm G}$. |
| − | * | + | |
| − | * | + | *This code is neither suitable for error correction nor for error detection because of $d_{\rm min} = 1$. Nevertheless, this code is also considered exemplarily in the next sections, because the coding results are well interpretable.<br> |
| + | |||
| + | *At this point we would like to draw your attention to the applet [[Applets:Gram-Schmidt-Verfahren|$\text{Gram–Schmidt process}$]] for the book "Digital Signal Transmission", which teaches the calculation of basis functions, although in a different context than the one used here.<br> | ||
| − | == | + | == Identical Codes == |
<br> | <br> | ||
| − | + | The vectors $\underline{g}_1$, $\underline{g}_2$, ... , $\underline{g}_k$ used in $\text{Example 4}$ in the last section are the [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#Orthonormal_basis_functions|$\text{basis vectors}$]] of the linear block code $\mathcal{C}$. | |
| + | *The code itself can be viewed as a $k$–dimensional subspace of $\text{GF}(2^n)$. | ||
| − | + | *The basis vectors $\underline{g}_1$, $\underline{g}_2$, ... , $\underline{g}_k$ are linearly independent.<br> | |
| + | |||
| + | |||
| + | However, the subspace $\mathcal{C}$ is not only spanned by the basis vectors | ||
::<math>\underline{g}_1 = (1, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm} | ::<math>\underline{g}_1 = (1, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm} | ||
| Line 171: | Line 194: | ||
\underline{g}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm}</math> | \underline{g}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm}</math> | ||
| − | + | but other basis vectors $\underline{g}\hspace{0.05cm}'_1$, $\underline{g}\hspace{0.05cm}'_2$ and $\underline{g}\hspace{0.05cm}'_3$ are equally suitable as long as linear independence is guaranteed between them.<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 5:}$ We compare the code $\mathcal{C}$ of [[Channel_Coding/General_Description_of_Linear_Block_Codes#Code_definition_by_the_generator_matrix|$\text{Example 4}$]] with a second code $\mathcal{C}\hspace{0.05cm}'$. The generator matrices are: |
::<math> \boldsymbol{\rm G} = \begin{pmatrix} | ::<math> \boldsymbol{\rm G} = \begin{pmatrix} | ||
| Line 197: | Line 220: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | *The two codes are identical: They contain the exact same code words; only a different assignment applies. | |
| + | |||
| + | *During the transition from $\boldsymbol{\rm G}$ to $\boldsymbol{\rm G}\hspace{0.05cm}'$, the following allowed operations were performed: | ||
::<math>\underline{g}\hspace{0.05cm}'_1 = \underline{g}_1 + \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} | ::<math>\underline{g}\hspace{0.05cm}'_1 = \underline{g}_1 + \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} | ||
| Line 203: | Line 228: | ||
\underline{g}\hspace{0.05cm}'_3 = \underline{g}_2 + \underline{g}_3 \hspace{0.05cm}.</math> | \underline{g}\hspace{0.05cm}'_3 = \underline{g}_2 + \underline{g}_3 \hspace{0.05cm}.</math> | ||
| − | + | *The corresponding code $\mathcal{C}'$ is obtained by the equation $\underline{x}' = \underline{u} \cdot \boldsymbol{\rm G}'$: | |
::<math>\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_0 = | ::<math>\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_0 = | ||
| Line 209: | Line 234: | ||
::<math>\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_1 = | ::<math>\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_1 = | ||
(0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{x}_3\hspace{0.05cm},</math> | (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{x}_3\hspace{0.05cm},</math> | ||
| − | ::<math>\underline{u}_2 | + | ::<math>\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_2 = |
(0, 1, 0, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_2\hspace{0.05cm},</math> | (0, 1, 0, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_2\hspace{0.05cm},</math> | ||
::<math>\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_3 = | ::<math>\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_3 = | ||
| Line 222: | Line 247: | ||
(1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_7\hspace{0.05cm}.</math> | (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_7\hspace{0.05cm}.</math> | ||
| − | + | *The corresponding code words $\underline{x}_i = \underline{u}_i \cdot \boldsymbol{\rm G}$ of the code $\mathcal{C}$ ⇒ generator matrix $\boldsymbol{\rm G}$ are give in $\text{Example 4}$ (previous section).}}<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ The code tables of $\text{Example 4}$ and $\text{Example 5}$ make clear: |
| − | *$\mathcal{C}$ | + | *$\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$ contain the same code words. They are thus "identical codes" and both have the same capability of correction (see next section).<br> |
| − | *$\mathcal{C}'$ | + | *$\mathcal{C}\hspace{0.05cm}'$ is now a "systematic code" since the first $k$ binary digits of each code word $\underline{x}\hspace{0.05cm}'_i$ match the binary digits of the information word.}}<br> |
| − | == | + | == Systematic Codes== |
<br> | <br> | ||
| − | + | The property "systematic" is now to be specified in mathematical form.<br> | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ In a $\text{systematic }(n, k) \text{ block code} \ \ \mathcal{C}$ each code word $\underline{x}$ explicitly includes the information word $\underline{u}$. |
| − | * | + | *That is, it applies: $\underline{u} = (u_1,\ u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm},\ u_k) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm} = |
| − | + | (u_1,\ u_2,\ ... \hspace{0.05cm},\ u_k,\ x_{k+1}, \hspace{0.05cm}\text{...}\hspace{0.05cm},\ x_n)\hspace{0.05cm}.$ | |
| − | (u_1, u_2, ... \hspace{0.05cm}, u_k, x_{k+1}, ... \hspace{0.05cm}, x_n)\hspace{0.05cm}. | ||
| − | * | + | *The generator matrix in this case has the form $\boldsymbol{\rm G_{\rm sys} } =\left({ \boldsymbol{\rm I}_{\rm k} \ ; \ \boldsymbol{\rm P} }\right)$ with the $k×k$ "identity matrix" $\boldsymbol{\rm I}_{\rm k}$ and a suitably chosen $(n-1)×k$ matrix $\boldsymbol{\rm P}$.}}<br> |
| − | + | So, for $\text{Example 5}$ in the last section can also be written: | |
| − | ::<math> \boldsymbol{\rm G_{sys}} =\left({ \boldsymbol{\rm I}}_3 \: ; \: { \boldsymbol{\rm P}}\right)\hspace{0.3cm}{\rm | + | ::<math> \boldsymbol{\rm G_{sys}} =\left({ \boldsymbol{\rm I}}_3 \: ; \: { \boldsymbol{\rm P}}\right)\hspace{0.3cm}{\rm with}\hspace{0.3cm} |
{ \boldsymbol{\rm I_{3}}} = \begin{pmatrix} | { \boldsymbol{\rm I_{3}}} = \begin{pmatrix} | ||
1 &0 &0 \\ | 1 &0 &0 \\ | ||
0 &1 &0 \\ | 0 &1 &0 \\ | ||
0 &0 &1 | 0 &0 &1 | ||
| − | \end{pmatrix}\hspace{0.3cm}{\rm | + | \end{pmatrix}\hspace{0.3cm}{\rm and}\hspace{0.3cm} |
{ \boldsymbol{\rm P}} = \begin{pmatrix} | { \boldsymbol{\rm P}} = \begin{pmatrix} | ||
0 &1 \\ | 0 &1 \\ | ||
| Line 256: | Line 280: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | It is gratifying from the point of view of channel coding, that for each code $\mathcal{C}$ a systematic $($identical or at least equivalent$)$ code $\mathcal{C}_{\rm sys}$ can be found.<br> | |
| + | In an »'''identical systematic code'''«, $\underline{x}$ and $\underline{x}_{\rm sys}$ contain the same code words, only the mapping $\underline{u} → \underline{x}$ is different. One gets from a block code $\mathcal{C}$ to the identical systematic code $\mathcal{C}_{\rm sys}$ by the following manipulations with respect to the generator matrix $\mathcal{\rm G}$: | ||
| + | *Swap or permute the rows,<br> | ||
| − | + | *Multiply all rows by a constant vector not equal to $\underline{0}$,<br> | |
| − | |||
| − | * | + | *Replace a row with a linear combination between this row and another one.<br> |
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Without proof:}$ An $\text{identical systematic code }\mathcal{C}_{\rm sys}$ can be found whenever to a generator matrix $\boldsymbol{\rm G}$ there exists a matrix $\boldsymbol{\rm A}$ such that $\boldsymbol{\rm G}_{\rm sys} = \boldsymbol{\rm A} \cdot \boldsymbol{\rm G}$ holds.}} |
| − | + | If this is not possible, one can at least find an »'''equivalent systematic code'''« by swapping or permuting the columns of $\boldsymbol{\rm G}$ : | |
| + | ::<math>\mathcal{C}_{\rm sys} = {\rm \pi} (\mathcal{C})\hspace{0.3cm}{\rm with}\hspace{0.3cm}{\rm \pi}():\hspace{0.15cm}{\rm permutation\:operator}\hspace{0.05cm}.</math> | ||
| − | + | *The codes $\mathcal{C}$ and $\mathcal{C}_{\rm sys}$ then contain different code words, but they exhibit the same properties. | |
| + | *For example, in this case $\mathcal{C}_{\rm sys}$ exhibits the same minimum Hamming distance $d_{\rm min}$ as the code $\mathcal{C}$.<br> | ||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 6:}$ We consider the generator matrices |
::<math> \boldsymbol{\rm G} = \begin{pmatrix} | ::<math> \boldsymbol{\rm G} = \begin{pmatrix} | ||
1 &1 &0 &0 \\ | 1 &1 &0 &0 \\ | ||
0 &0 &1 &1 | 0 &0 &1 &1 | ||
| − | \end{pmatrix} | + | \end{pmatrix},\hspace{0.3cm} |
\boldsymbol{\rm G_{sys} } = \begin{pmatrix} | \boldsymbol{\rm G_{sys} } = \begin{pmatrix} | ||
1 &0 &1 &0 \\ | 1 &0 &1 &0 \\ | ||
| Line 289: | Line 313: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | The analysis shows: | |
| − | * | + | *The corresponding codes $\mathcal{C}$ and $\mathcal{C}_{\rm sys}$ contain different code words and are thus »'''not identical'''«: |
| − | ::<math>\mathcal{C} = \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 0, 1, 1) \hspace{0.05cm},(1, 1, 0, 0) \hspace{0.05cm},(1, 1, 1, 1) \}\hspace{0.05cm},</math> | + | ::<math>\mathcal{C} = \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 0, 1, 1) \hspace{0.05cm},(1, 1, 0, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm},</math> |
| − | ::<math>\mathcal{C}_{\rm sys}= \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 1, 0, 1) \hspace{0.05cm},(1, 0, 1, 0) \hspace{0.05cm},(1, 1, 1, 1) \}\hspace{0.05cm}.</math> | + | ::<math>\mathcal{C}_{\rm sys}= \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 1, 0, 1) \hspace{0.05cm},(1, 0, 1, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm}.</math> |
| − | * | + | *But they are »'''equivalent'''«: $\boldsymbol{\rm G}_{\rm sys}$ is obtained from $\boldsymbol{\rm G}$ by swapping the second and third columns. |
| − | |||
| + | *It is a $\text{(4, 2, 2)}$ block code in both cases ⇒ $d_{\rm min} = 2$.}} | ||
| − | == | + | |
| + | == Relationship between generator and parity-check matrix== | ||
<br> | <br> | ||
| − | + | To define these two description matrices, we assume the following equations: | |
::<math>\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ::<math>\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| Line 306: | Line 331: | ||
{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T} = { \boldsymbol{\rm 0}}\hspace{0.05cm}.</math> | { \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T} = { \boldsymbol{\rm 0}}\hspace{0.05cm}.</math> | ||
| − | + | Linking these two equations, we get: | |
| − | :<math>{ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} | + | ::<math>{ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} |
\forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} | \forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.</math> | \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.</math> | ||
| − | + | Note that in these equations. | |
| − | *$\underline{0}$ | + | *$\underline{0}$ denotes a row vector with $k$ elements, and |
| − | *$\boldsymbol{\rm 0}$ | + | *$\boldsymbol{\rm 0}$ denotes a matrix with $m$ rows and $k$ columns, |
| − | + | where all elements of $\underline{0}$ and $\boldsymbol{\rm 0}$ are zero.<br> | |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 7:}$ We consider as in [[Channel_Coding/General_Description_of_Linear_Block_Codes#Code_definition_by_the_generator_matrix|$\text{Example 4}$]] the $\text{(5, 3)}$ block code |
| − | :<math>\mathcal{C} = \{ \hspace{0.15cm} ( \hspace{0.05cm} 0, 0, 0, 0, 0) \hspace{0.05cm},</math> | + | :<math>\mathcal{C} = \big \{ \hspace{0.15cm} ( \hspace{0.05cm} 0, 0, 0, 0, 0) \hspace{0.05cm},</math> |
::<math> \hspace{0.6cm}( \hspace{0.05cm} 0, 1, 1, 1, 0) \hspace{0.05cm},</math> | ::<math> \hspace{0.6cm}( \hspace{0.05cm} 0, 1, 1, 1, 0) \hspace{0.05cm},</math> | ||
::<math> \hspace{0.6cm}( \hspace{0.05cm}0, 1, 0, 1, 0) \hspace{0.05cm},</math> | ::<math> \hspace{0.6cm}( \hspace{0.05cm}0, 1, 0, 1, 0) \hspace{0.05cm},</math> | ||
| Line 329: | Line 354: | ||
::<math> \hspace{0.6cm}( \hspace{0.05cm}1, 0, 1, 0, 1) \hspace{0.05cm},</math> | ::<math> \hspace{0.6cm}( \hspace{0.05cm}1, 0, 1, 0, 1) \hspace{0.05cm},</math> | ||
::<math> \hspace{0.6cm}( \hspace{0.05cm}1, 0, 0, 0, 1) \hspace{0.05cm},</math> | ::<math> \hspace{0.6cm}( \hspace{0.05cm}1, 0, 0, 0, 1) \hspace{0.05cm},</math> | ||
| − | ::<math> \hspace{0.6cm}(\hspace{0.05cm}1, 1, 1, 1, 1) \}\hspace{0.05cm}.</math> | + | ::<math> \hspace{0.6cm}(\hspace{0.05cm}1, 1, 1, 1, 1) \big \}\hspace{0.05cm}.</math> |
| − | + | From $n= 5$ and $k = 3$ follows for the number of parity-check equations $m = 2$. By analyzing the possible code words, the following results are obtained: | |
::<math>x_1 \oplus x_5 = 0 \hspace{0.05cm},\hspace{0.5cm} | ::<math>x_1 \oplus x_5 = 0 \hspace{0.05cm},\hspace{0.5cm} | ||
| Line 357: | Line 382: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | The zero matrix here consists of $m = 2$ rows and $k = 3$ columns. For example, for the element in the first row and the first column: | |
::<math>1 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} | ::<math>1 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} | ||
| Line 368: | Line 393: | ||
| − | == | + | == Generator matrix vs. parity-check matrix for systematic codes == |
<br> | <br> | ||
| − | + | Generally, $\boldsymbol{\rm G}$ and $\boldsymbol{\rm H}$ cannot be directly converted into each other, because of the different dimensions of generator matrix $(k \times n)$ and parity-check matrix $(m \times n)$.<br> | |
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Without proof:}$ | ||
| + | The calculation process is simplified if the $(k \times n)$ generator matrix is in systematic form: | ||
| + | :$$ \boldsymbol{\rm G_{sys} } =\left({ \boldsymbol{\rm I} }_k \: ; \: { \boldsymbol{\rm P} }\right).$$ | ||
| + | *Then it follows from $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$ for the $(m \times n)$ parity-check matrix with $m = n-k$: | ||
| − | ::<math>{ \boldsymbol{\rm H}} =\left(-{ \boldsymbol{\rm P}}^{\rm T} \: ; \: { \boldsymbol{\rm I}}_m \right) | + | ::<math>{ \boldsymbol{\rm H} } =\left( - { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right) |
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | *This equation holds in general, i.e., also in the non-binary case. Since we restrict ourselves to binary codes ⇒ $\mathcal{C} \in \text{GF}(2^n)$ ⇒ $ - \boldsymbol{\rm P} = +\boldsymbol{\rm P}$. | |
| + | |||
| + | *Thus we obtain the form we will use in the remainder of this chapter.<br> | ||
| + | |||
| + | ::<math>{ \boldsymbol{\rm H} } =\left( { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right)\hspace{0.05cm}. | ||
| + | </math>}} | ||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 8:}$ We continue to consider the example $\text{(5, 3)}$ block code, but now assume the systematic generator matrix $\boldsymbol{\rm G}_{\rm sys}$ that we determined the [[Channel_Coding/General_Description_of_Linear_Block_Codes#Identical_Codes|$\text{Example 5}$]]: |
::<math> \boldsymbol{\rm G_{sys} } = \begin{pmatrix} | ::<math> \boldsymbol{\rm G_{sys} } = \begin{pmatrix} | ||
| Line 407: | Line 439: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | *This gives the following for the parity-check matrix | |
::<math>{ \boldsymbol{\rm H} } =\left({ \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_2 \right) | ::<math>{ \boldsymbol{\rm H} } =\left({ \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_2 \right) | ||
| Line 414: | Line 446: | ||
1 &0 &0 &0 &1 | 1 &0 &0 &0 &1 | ||
\end{pmatrix} | \end{pmatrix} | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}.</math> |
| − | + | *The following code table results: | |
::<math>\underline{u}_0 = (0, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_0 = | ::<math>\underline{u}_0 = (0, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_0 = | ||
| Line 431: | Line 463: | ||
(1, 1, 1, 1, 1) \hspace{0.05cm}.</math> | (1, 1, 1, 1, 1) \hspace{0.05cm}.</math> | ||
| − | + | *Together with the vector $\underline{x} = (u_1,\ u_2,\ u_3,\ p_1,\ p_2) = (x_1,\ x_2,\ x_3,\ x_4,\ x_5)$ the parity bits are then: | |
::<math>p_1 = u_2 \hspace{0.05cm},\hspace{0.2cm}p_2 = u_1 \hspace{0.05cm},</math> | ::<math>p_1 = u_2 \hspace{0.05cm},\hspace{0.2cm}p_2 = u_1 \hspace{0.05cm},</math> | ||
| − | + | and the corresponding parity-check equations of the decoder: | |
| − | :<math>x_2 + x_4 = 0 \hspace{0.05cm},\hspace{0.2cm}x_1 + x_5 = 0 \hspace{0.05cm}.</math> | + | ::<math>x_2 + x_4 = 0 \hspace{0.05cm},\hspace{0.2cm}x_1 + x_5 = 0 \hspace{0.05cm}.</math> |
| − | + | You can see from these equations and from the above code table: | |
| − | + | #This code offers no protection against a transmission error with respect to the third bit $(x_3 = u_3)$ . | |
| − | + | #This, of course, does not allow for error detection, and much less error correction. | |
| − | + | #But the same is true for the non-systematic code according to [[Channel_Coding/General_Description_of_Linear_Block_Codes#Relationship_between_generator_and_parity-check_matrix|$\text{Example 7}$]] in the last section.}}<br> | |
| − | == | + | == Representation of SPC and RC as dual codes == |
<br> | <br> | ||
| − | + | For the codes already dealt with in the chapter [[Channel_Coding/Examples_of_Binary_Block_Codes|$\text{Examples of binary block codes}$]], the generator matrix $\boldsymbol{\rm G}$ and the parity-check matrix $\boldsymbol{\rm H}$ are to be given in each case. Let the code length always be $n = 5$ for the following examples, but the results can be interpreted in the same way for other code lengths. It applies to | |
| − | * | + | *the [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes|$\text{single parity–check code}$]] ⇒ $\text{SPC (5, 4)}$: |
::<math>{ \boldsymbol{\rm H}} | ::<math>{ \boldsymbol{\rm H}} | ||
| Line 460: | Line 492: | ||
0 &0 &0 &1 &1 | 0 &0 &0 &1 &1 | ||
\end{pmatrix} | \end{pmatrix} | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm};</math> |
| − | * | + | *the [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|$\text{repetition code}$]] ⇒ $\text{RC (5, 1)}$: |
::<math>{ \boldsymbol{\rm G}} | ::<math>{ \boldsymbol{\rm G}} | ||
| Line 477: | Line 509: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | + | The first equation can be easily derived from the respective definition and the derived equation follows from the relation $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$. | |
| − | * | + | |
| + | From the above matrices can be generalized: | ||
| + | *The generator matrix of the $\text{RC (5, 1)}$ is identical to the parity-check matrix of the $\text{SPC (5, 4)}$. In each case they are $(5 \times 1)$ matrices.<br> | ||
| − | * | + | *The parity-check matrix of the $\text{RC (5, 1)}$ is identical to the generator matrix of the $\text{SPC (5, 4)}$. These two matrices each have $5$ columns and $4$ rows.<br> |
| − | * | + | *This situation arises because we are dealing here with so-called "dual codes". For explanation we need two more definitions:<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Two linear codes $\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$, both made of ${\rm GF}(2^n)$, are »'''orthogonal'''« if all code words $\underline{x} \in \mathcal{C}$ to all code words $\underline{x}\hspace{0.05cm}' \in \mathcal{C}\hspace{0.05cm}'$ are orthogonal. |
| + | *One then refers to $\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$ as »'''dual codes'''«.}}<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Two code words $\underline{x} \in{\rm GF}(2^n)$ and $\underline{x\hspace{0.05cm}'} \in {\rm GF}(2^n)$ are »'''orthogonal'''« to each other whenever the [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#Nomenclature_in_the_fourth_chapter|$\text{inner product}$]] disappears: |
| − | ::<math>\ | + | ::<math>\big \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \big \rangle = \sum_{i=1 }^{n} x_i \cdot x\hspace{0.05cm}'_i = 0 \hspace{0.05cm}, \hspace{0.5cm} |
| − | \left \langle \underline{x} \cdot \underline{x}' \right \rangle \in {\rm GF}(2^n) | + | \left \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \right \rangle \in {\rm GF}(2^n) |
\hspace{0.05cm}.</math>}}<br> | \hspace{0.05cm}.</math>}}<br> | ||
| − | + | Because of the product in ${\rm GF}(2^n)$, the following code word pairs are also orthogonal to each other: | |
| − | ::<math>\left \langle \hspace{0.05cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (1, 1, 1, 0) \hspace{0.05cm} \right \rangle = 0\hspace{0.05cm},\hspace{0. | + | ::<math>\left \langle \hspace{0.05cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (1, 1, 1, 0) \hspace{0.05cm} \right \rangle = 0\hspace{0.05cm},\hspace{0.8cm} |
\left \langle \hspace{0.1cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (0, 1, 1, 0) \hspace{0.1cm}\right \rangle = 0\hspace{0.05cm}.</math> | \left \langle \hspace{0.1cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (0, 1, 1, 0) \hspace{0.1cm}\right \rangle = 0\hspace{0.05cm}.</math> | ||
| − | + | *The code $\mathcal{C}$ spans a $k$–dimensional subvector space in ${\rm GF}(2^n)$. | |
| + | |||
| + | *The subspace of the dual code $\mathcal{C}\hspace{0.05cm}'$ is orthogonal to it and has dimension $n-k$. | ||
| − | == | + | *Thus follows: ${\rm dim} \{ \mathcal{C} \} + {\rm dim} \{ \mathcal{C}\hspace{0.05cm}' \} = n\hspace{0.05cm}.$<br> |
| + | |||
| + | == Some properties of the (7, 4, 3) Hamming code == | ||
<br> | <br> | ||
| − | + | Let us summarize again the previous results of this chapter using the example of the systematic Hamming code, which has already been described in detail in the chapter [[Channel_Coding/Examples_of_Binary_Block_Codes#Hamming_Codes|$\text{Examples of Binary Block Codes}$]] . This $\text{(7, 4, 3)}$ code is characterized by | |
| − | [[File:P ID2359 KC T 1 4 S7.png|right|frame| | + | [[File:P ID2359 KC T 1 4 S7.png|right|frame|Code words of the $\text{HC (7, 4, 3)}$|class=fit]] |
| − | * | + | *the number of parity-check equations $m = 3$,<br> |
| − | * | + | *the code length $n = 2^m-1 = 7$,<br> |
| − | * | + | *the information word length $k = n-m = 4$,<br> |
| − | * | + | *the number of code words (dimension) $2^k =16$ ,<br> |
| − | * | + | *the rate $R= k/n = 4/7$,<br> |
| − | * | + | *the minimum distance $d_{\rm min} = 3$ $($independent of $m$, $n$ and $k)$.<br> |
| + | |||
| + | |||
| + | In the above table the $2^4 = 16$ code words are given <br>(black: four information bits, red: three parity bits). | ||
| + | |||
| + | One can see from this: | ||
| + | *The code includes both the all zero word "$0000000$" and the all one word "$1111111$". | ||
| + | |||
| + | *There are seven code words resulting from "$0001011$" each by cyclic shift (all highlighted in yellow). | ||
| + | *There are seven code words resulting from "$0011101$" each by cyclic shift (all highlighted in green). | ||
| − | + | *For each code word also exists the "negated" code word, for example, besides "$0001011$" there is also the code word "$1110100$". | |
| − | + | *The parity-check matrix can be written as follows: | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
::<math>{ \boldsymbol{\rm H}} = \begin{pmatrix} | ::<math>{ \boldsymbol{\rm H}} = \begin{pmatrix} | ||
| Line 539: | Line 582: | ||
\end{pmatrix}\hspace{0.05cm}.</math> | \end{pmatrix}\hspace{0.05cm}.</math> | ||
| − | + | *Accordingly, the following applies to the generator matrix: | |
::<math>{ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_4 \: ; \: { \boldsymbol{\rm P}}\right) | ::<math>{ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_4 \: ; \: { \boldsymbol{\rm P}}\right) | ||
| Line 549: | Line 592: | ||
\end{pmatrix}\hspace{0.05cm}.</math><br> | \end{pmatrix}\hspace{0.05cm}.</math><br> | ||
| − | == | + | == Exercises for the chapter == |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_1.07:_Check_and_Generator_Matrix_of_the_HC_(7,_4,_3)|Exercise 1.7: Check and Generator Matrix of the HC (7, 4, 3)]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.07Z:_Klassifizierung_von_Blockcodes|Exercise 1.7Z: Classification of Block Codes]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.08:_Identische_Codes|Exercise 1.8: Identical Codes]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.08Z:_Äquivalente_Codes|Exercise 1.8Z: Equivalent Codes]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.09:_Erweiterter_Hamming–Code|Exercise 1.9: Extended Hamming Code]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.09Z:_Erweiterung_und/oder_Punktierung|Exercise 1.9Z: Extension and/or Puncturing]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.10:_Einige_Generatormatrizen|Exercise 1.10: Some Generator Matrices]] |
{{Display}} | {{Display}} | ||
Latest revision as of 10:32, 22 November 2022
Contents
- 1 Linear codes and cyclic codes
- 2 Code definition by the parity-check matrix
- 3 Code definition by the generator matrix
- 4 Identical Codes
- 5 Systematic Codes
- 6 Relationship between generator and parity-check matrix
- 7 Generator matrix vs. parity-check matrix for systematic codes
- 8 Representation of SPC and RC as dual codes
- 9 Some properties of the (7, 4, 3) Hamming code
- 10 Exercises for the chapter
Linear codes and cyclic codes
All codes mentioned so far are »linear«:
- the $\text{single parity-check code}$ $\rm (SPC)$,
- the $\text{repetition code}$ $\rm (RC)$,
- the $\text{Hamming code}$ $\rm (HC)$.
Now the definition of "linearity" valid for binary block codes is added.
$\text{Definition:}$ A »linear binary block code« $\mathcal{C}$ is a set of $2^k$ code words $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$, where the (modulo 2) sum of any two code words $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ again gives a valid code word:
- \[\underline{x}, \underline{x}\hspace{0.05cm}' \in {\rm GF}(2^n),\hspace{0.3cm} \underline{x}, \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x} + \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.05cm}.\]
- This condition must also be satisfied for $\underline{x} = \underline{x}\hspace{0.05cm}'$ .
- For the remainder of this book, modulo addition will no longer be expressed by the "modulo sign" to simplify notation, but by the conventional "plus sign".
$\text{Example 1:}$ We consider two $\text{(3, 2)}$ block codes:
- \[\mathcal{C}_1 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 0, 1) \hspace{0.05cm},(1, 1, 0) \}\hspace{0.05cm},\]
- \[\mathcal{C}_2 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 1, 0) \hspace{0.05cm},(1, 1, 1) \hspace{0.05cm}.\]
You can see:
- The code $\mathcal{C}_1$ is linear, since the modulo 2 addition of any two code words always yields also a valid code word, e.g. $(0, 1, 1) + (1, 0, 1) = (1, 1, 0)$.
- The above definition also applies to the modulo 2 addition of a code word with itself, e.g. $(0, 1, 1) + (0, 1, 1) = (0, 0, 0)$.
- From this follows: Each linear code contains the all-zero word $\underline{0}$.
- Although the last condition is satisfied, $\mathcal{C}_2$ is not a linear code. Indeed, for this code: $(0, 1, 1) + (1, 1, 0) = (1, 0, 1)$. This is not a valid code word of $\mathcal{C}_2$.
In the following, we restrict ourselves exclusively to linear codes, since non-linear codes are of secondary importance for practical use.
$\text{Definition:}$ A linear block code $\mathcal{C}$ is called »cyclic« if every cyclic shift of a code word $\underline{x}$ $($to the left or right$)$ results in a valid code word:
- \[\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x}\hspace{0.05cm}'= (x_n, x_1, \hspace{0.05cm}\text{...} \hspace{0.05cm} \hspace{0.05cm}, x_{n-1}) \in \mathcal{C} \hspace{0.05cm}.\]
$\text{Example 2:}$ You can see from the table for the $\text{HC (7, 4, 3)}$ that it is linear and cyclic.
- A valid code word results even if all bits are inverted: $0 ↔ 1$.
- Also the $\underline{0}$ word $(n$ times a "zero"$)$ and the $\underline{1}$ word $(n$ times a "one"$)$ are allowed with this code.
Code definition by the parity-check matrix
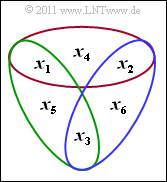
We consider the $\text{(7, 4, 3)}$ Hamming code with code words $\underline{x}$ of length $n=7$, consisting of
- $k = 4$ information bits $x_1$, $x_2$, $x_3$, $x_4$, and
- $m = n-k = 3$ parity bits $x_5$, $x_6$, $x_7$.
The parity-check equations are (see graphic on the right):
- \[x_1 + x_2 + x_3 + x_5 = 0 \hspace{0.05cm},\]
- \[x_2 + x_3 + x_4 + x_6 = 0 \hspace{0.05cm},\]
- \[x_1 + x_2 + x_4 + x_7 = 0 \hspace{0.05cm}. \]
In matrix notation, this set of equations reads:
- \[{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}. \]
In this equation are used:
- the »parity-check matrix« ${ \boldsymbol{\rm H}}$ with $m = n-k = 3$ rows and $n = 7$ columns:
- \[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 & 0 & 0\\ 0 &1 &1 &1 &0 & 1 & 0\\ 1 &1 &0 &1 &0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]
- the code word $\underline{x}= (x_1,\ x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm},\ x_7)$ of length $n = 7$,
- the all-zero vector $\underline{0} = (0,\ 0,\ 0)$ of length $m = 3$.
By "transposing", the row vectors $\underline{x}$ and $\underline{0}$ become the corresponding column vectors $\underline{x}^{\rm T}$ and $\underline{0}^{\rm T}$.
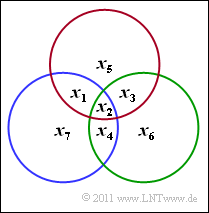
$\text{Example 3:}$ The graph illustrates the $m = 3$ parity-check equations of a code $\mathcal{C}$ with code parameters $n = 6$ and $k = 3$ in the order red, green and blue. Thus, $\mathcal{C}$ is not a Hamming code $(n \ne 2^m-1)$.
According to the equation $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T}$ the parity-check matrix is:
- \[ \boldsymbol{\rm H} = \begin{pmatrix} 1 &1 &0 &1 &0 & 0\\ 1 &0 &1 &0 &1 & 0\\ 0 &1 &1 &0 &0 & 1 \end{pmatrix}\hspace{0.05cm}.\]
The $2^k = 8$ code words in systematic realization are (with the parity bits to the right of the small arrow):
\[\underline{x}_0 = (0,\ 0,\ 0_{\hspace{0.01cm} \rightarrow} 0,\ 0,\ 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_1 = (0,\ 0,\ 1_{\hspace{0.01cm} \rightarrow}0,\ 1,\ 1)\hspace{0.05cm},\hspace{0.5cm} \underline{x}_2 = (0,\ 1,\ 0_{\hspace{0.01cm} \rightarrow}1,\ 0,\ 1)\hspace{0.05cm},\hspace{0.5cm}\underline{x}_3 = (0, 1, 1_{\hspace{0.01cm} \rightarrow}1,\ 1,\ 0)\hspace{0.05cm}, \] \[\underline{x}_4 = (1,\ 0,\ 0_{\hspace{0.01cm} \rightarrow} 1,\ 1,\ 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_5 = (1,\ 0,\ 1_{\hspace{0.01cm} \rightarrow}1,\ 0,\ 1)\hspace{0.05cm},\hspace{0.5cm} \underline{x}_6 = (1,\ 1,\ 0_{\hspace{0.01cm} \rightarrow}0,\ 1,\ 1)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_7 = (1,\ 1,\ 1_{\hspace{0.01cm} \rightarrow}0,\ 0,\ 0)\hspace{0.05cm}.\]
It can be seen from these specifications:
- The number of columns $\boldsymbol{\rm H}$ is equal to the code length $n$.
- The number of lines of $\boldsymbol{\rm H}$ is equal to the number $m = n-k$ of parity-check equations.
- From $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} $ it therefore does not follow that all code words contain an even number of ones.
Code definition by the generator matrix
The check matrix $\boldsymbol{\rm H}$ of a $(n, k)$ block code has
- $n$ columns,
- $m = n-k$ rows.
However, the same code can be described by the matrix $\boldsymbol{\rm G}$ with
- also $n$ columns,
- but $k$ rows.
$\text{Definition:}$ A linear binary block code $\mathcal{C}$ can be characterized by the »check matrix« $\boldsymbol{\rm H}$ or with the »generator matrix« $\boldsymbol{\rm G}$ as follows:
- \[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\text{:} \hspace{0.2cm}{ \boldsymbol{\rm H} } \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \}\hspace{0.05cm},\]
- \[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{0.05cm}, \hspace{0.1cm}\underline{u} \in {\rm GF}(2^k)\text{:} \hspace{0.2cm}\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G} } \}\hspace{0.05cm}.\]
Before we turn to the properties of the generator matrix, we describe the generation of the code words with an example.
$\text{Example 4:}$ We consider a linear $(5, 3)$ block code with the generator matrix (again: this is not a Hamming code!)
- \[ \boldsymbol{\rm G} = \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix} \hspace{0.05cm}.\]
- Thus, the information words $\underline{u}= (u_1,\ u_2,\ u_3)$ are assigned to the code words $\underline{x}= (x_1,\ x_2,\ x_3,\ x_4,\ x_5)$ according to the following equations.
- The following always applies: $\underline{x} = \underline{u} \cdot \boldsymbol{\rm G}$:
- \[\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},\]
- \[\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_1 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{g}_3\hspace{0.05cm},\]
- \[\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_2 = (0, 1, 0, 1, 0)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2\hspace{0.05cm},\]
- \[\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_3 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2+\underline{g}_3\hspace{0.05cm},\]
- \[\underline{u}_4 = (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_4 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1 \hspace{0.05cm},\]
- \[\underline{u}_5 =(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_3\hspace{0.05cm},\]
- \[\underline{u}_6 = (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_6 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_2\hspace{0.05cm},\]
- \[\underline{u}_7 =(1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+ \underline{g}_2+\underline{g}_3\hspace{0.05cm}.\]
Notes:
- The basis vectors used here for the calculation $\underline{g}_1$, $\underline{g}_2$ and $\underline{g}_3$ – each with length $n = 5$ – correspond to the $k = 3$ rows of the generator matrix $\boldsymbol{\rm G}$.
- This code is neither suitable for error correction nor for error detection because of $d_{\rm min} = 1$. Nevertheless, this code is also considered exemplarily in the next sections, because the coding results are well interpretable.
- At this point we would like to draw your attention to the applet $\text{Gram–Schmidt process}$ for the book "Digital Signal Transmission", which teaches the calculation of basis functions, although in a different context than the one used here.
Identical Codes
The vectors $\underline{g}_1$, $\underline{g}_2$, ... , $\underline{g}_k$ used in $\text{Example 4}$ in the last section are the $\text{basis vectors}$ of the linear block code $\mathcal{C}$.
- The code itself can be viewed as a $k$–dimensional subspace of $\text{GF}(2^n)$.
- The basis vectors $\underline{g}_1$, $\underline{g}_2$, ... , $\underline{g}_k$ are linearly independent.
However, the subspace $\mathcal{C}$ is not only spanned by the basis vectors
- \[\underline{g}_1 = (1, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm}\]
but other basis vectors $\underline{g}\hspace{0.05cm}'_1$, $\underline{g}\hspace{0.05cm}'_2$ and $\underline{g}\hspace{0.05cm}'_3$ are equally suitable as long as linear independence is guaranteed between them.
$\text{Example 5:}$ We compare the code $\mathcal{C}$ of $\text{Example 4}$ with a second code $\mathcal{C}\hspace{0.05cm}'$. The generator matrices are:
- \[ \boldsymbol{\rm G} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix}= \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} \boldsymbol{\rm G}\hspace{0.05cm}' = \begin{pmatrix} \underline{g}\hspace{0.05cm}'_1\\ \underline{g}\hspace{0.05cm}'_2\\ \underline{g}\hspace{0.05cm}'_3\\ \end{pmatrix}= \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]
- The two codes are identical: They contain the exact same code words; only a different assignment applies.
- During the transition from $\boldsymbol{\rm G}$ to $\boldsymbol{\rm G}\hspace{0.05cm}'$, the following allowed operations were performed:
- \[\underline{g}\hspace{0.05cm}'_1 = \underline{g}_1 + \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_2 = \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_3 = \underline{g}_2 + \underline{g}_3 \hspace{0.05cm}.\]
- The corresponding code $\mathcal{C}'$ is obtained by the equation $\underline{x}' = \underline{u} \cdot \boldsymbol{\rm G}'$:
- \[\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_0 = (0, 0, 0, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_0 \hspace{0.05cm},\]
- \[\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_1 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{x}_3\hspace{0.05cm},\]
- \[\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_2 = (0, 1, 0, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_2\hspace{0.05cm},\]
- \[\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_3 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_1\hspace{0.05cm},\]
- \[\underline{u}_4 = (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_4 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_6 \hspace{0.05cm},\]
- \[\underline{u}_5 =(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_5\hspace{0.05cm},\]
- \[\underline{u}_6 = (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_6 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_4\hspace{0.05cm},\]
- \[\underline{u}_7 = (1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_7\hspace{0.05cm}.\]
- The corresponding code words $\underline{x}_i = \underline{u}_i \cdot \boldsymbol{\rm G}$ of the code $\mathcal{C}$ ⇒ generator matrix $\boldsymbol{\rm G}$ are give in $\text{Example 4}$ (previous section).
$\text{Conclusion:}$ The code tables of $\text{Example 4}$ and $\text{Example 5}$ make clear:
- $\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$ contain the same code words. They are thus "identical codes" and both have the same capability of correction (see next section).
- $\mathcal{C}\hspace{0.05cm}'$ is now a "systematic code" since the first $k$ binary digits of each code word $\underline{x}\hspace{0.05cm}'_i$ match the binary digits of the information word.
Systematic Codes
The property "systematic" is now to be specified in mathematical form.
$\text{Definition:}$ In a $\text{systematic }(n, k) \text{ block code} \ \ \mathcal{C}$ each code word $\underline{x}$ explicitly includes the information word $\underline{u}$.
- That is, it applies: $\underline{u} = (u_1,\ u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm},\ u_k) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm} = (u_1,\ u_2,\ ... \hspace{0.05cm},\ u_k,\ x_{k+1}, \hspace{0.05cm}\text{...}\hspace{0.05cm},\ x_n)\hspace{0.05cm}.$
- The generator matrix in this case has the form $\boldsymbol{\rm G_{\rm sys} } =\left({ \boldsymbol{\rm I}_{\rm k} \ ; \ \boldsymbol{\rm P} }\right)$ with the $k×k$ "identity matrix" $\boldsymbol{\rm I}_{\rm k}$ and a suitably chosen $(n-1)×k$ matrix $\boldsymbol{\rm P}$.
So, for $\text{Example 5}$ in the last section can also be written:
- \[ \boldsymbol{\rm G_{sys}} =\left({ \boldsymbol{\rm I}}_3 \: ; \: { \boldsymbol{\rm P}}\right)\hspace{0.3cm}{\rm with}\hspace{0.3cm} { \boldsymbol{\rm I_{3}}} = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.3cm}{\rm and}\hspace{0.3cm} { \boldsymbol{\rm P}} = \begin{pmatrix} 0 &1 \\ 1 &0 \\ 0 &0 \end{pmatrix}\hspace{0.05cm}.\]
It is gratifying from the point of view of channel coding, that for each code $\mathcal{C}$ a systematic $($identical or at least equivalent$)$ code $\mathcal{C}_{\rm sys}$ can be found.
In an »identical systematic code«, $\underline{x}$ and $\underline{x}_{\rm sys}$ contain the same code words, only the mapping $\underline{u} → \underline{x}$ is different. One gets from a block code $\mathcal{C}$ to the identical systematic code $\mathcal{C}_{\rm sys}$ by the following manipulations with respect to the generator matrix $\mathcal{\rm G}$:
- Swap or permute the rows,
- Multiply all rows by a constant vector not equal to $\underline{0}$,
- Replace a row with a linear combination between this row and another one.
$\text{Without proof:}$ An $\text{identical systematic code }\mathcal{C}_{\rm sys}$ can be found whenever to a generator matrix $\boldsymbol{\rm G}$ there exists a matrix $\boldsymbol{\rm A}$ such that $\boldsymbol{\rm G}_{\rm sys} = \boldsymbol{\rm A} \cdot \boldsymbol{\rm G}$ holds.
If this is not possible, one can at least find an »equivalent systematic code« by swapping or permuting the columns of $\boldsymbol{\rm G}$ :
- \[\mathcal{C}_{\rm sys} = {\rm \pi} (\mathcal{C})\hspace{0.3cm}{\rm with}\hspace{0.3cm}{\rm \pi}():\hspace{0.15cm}{\rm permutation\:operator}\hspace{0.05cm}.\]
- The codes $\mathcal{C}$ and $\mathcal{C}_{\rm sys}$ then contain different code words, but they exhibit the same properties.
- For example, in this case $\mathcal{C}_{\rm sys}$ exhibits the same minimum Hamming distance $d_{\rm min}$ as the code $\mathcal{C}$.
$\text{Example 6:}$ We consider the generator matrices
- \[ \boldsymbol{\rm G} = \begin{pmatrix} 1 &1 &0 &0 \\ 0 &0 &1 &1 \end{pmatrix},\hspace{0.3cm} \boldsymbol{\rm G_{sys} } = \begin{pmatrix} 1 &0 &1 &0 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.\]
The analysis shows:
- The corresponding codes $\mathcal{C}$ and $\mathcal{C}_{\rm sys}$ contain different code words and are thus »not identical«:
- \[\mathcal{C} = \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 0, 1, 1) \hspace{0.05cm},(1, 1, 0, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm},\]
- \[\mathcal{C}_{\rm sys}= \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 1, 0, 1) \hspace{0.05cm},(1, 0, 1, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm}.\]
- But they are »equivalent«: $\boldsymbol{\rm G}_{\rm sys}$ is obtained from $\boldsymbol{\rm G}$ by swapping the second and third columns.
- It is a $\text{(4, 2, 2)}$ block code in both cases ⇒ $d_{\rm min} = 2$.
Relationship between generator and parity-check matrix
To define these two description matrices, we assume the following equations:
- \[\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x}^{\rm T} = { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} \hspace{0.05cm}, \hspace{0.8cm} { \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T} = { \boldsymbol{\rm 0}}\hspace{0.05cm}.\]
Linking these two equations, we get:
- \[{ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} \forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.\]
Note that in these equations.
- $\underline{0}$ denotes a row vector with $k$ elements, and
- $\boldsymbol{\rm 0}$ denotes a matrix with $m$ rows and $k$ columns,
where all elements of $\underline{0}$ and $\boldsymbol{\rm 0}$ are zero.
$\text{Example 7:}$ We consider as in $\text{Example 4}$ the $\text{(5, 3)}$ block code
\[\mathcal{C} = \big \{ \hspace{0.15cm} ( \hspace{0.05cm} 0, 0, 0, 0, 0) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}( \hspace{0.05cm} 0, 1, 1, 1, 0) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}( \hspace{0.05cm}0, 1, 0, 1, 0) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}( \hspace{0.05cm}0, 0, 1, 0, 0) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}( \hspace{0.05cm} 1, 1, 0, 1, 1) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}( \hspace{0.05cm}1, 0, 1, 0, 1) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}( \hspace{0.05cm}1, 0, 0, 0, 1) \hspace{0.05cm},\]
- \[ \hspace{0.6cm}(\hspace{0.05cm}1, 1, 1, 1, 1) \big \}\hspace{0.05cm}.\]
From $n= 5$ and $k = 3$ follows for the number of parity-check equations $m = 2$. By analyzing the possible code words, the following results are obtained:
- \[x_1 \oplus x_5 = 0 \hspace{0.05cm},\hspace{0.5cm} x_2 \oplus x_4 = 0\hspace{1cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0 \end{pmatrix}\]
- \[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} } \cdot { \boldsymbol{\rm G} }^{\rm T} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0 \end{pmatrix} \begin{pmatrix} 1 &0 &0 \\ 1 &1 &1 \\ 0 &0 &1 \\ 1 &1 &1 \\ 1 &0 &0 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \\ 0 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]
The zero matrix here consists of $m = 2$ rows and $k = 3$ columns. For example, for the element in the first row and the first column:
- \[1 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 0 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 1 \cdot 1 = 0 \hspace{0.05cm}.\]
Generator matrix vs. parity-check matrix for systematic codes
Generally, $\boldsymbol{\rm G}$ and $\boldsymbol{\rm H}$ cannot be directly converted into each other, because of the different dimensions of generator matrix $(k \times n)$ and parity-check matrix $(m \times n)$.
$\text{Without proof:}$ The calculation process is simplified if the $(k \times n)$ generator matrix is in systematic form:
- $$ \boldsymbol{\rm G_{sys} } =\left({ \boldsymbol{\rm I} }_k \: ; \: { \boldsymbol{\rm P} }\right).$$
- Then it follows from $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$ for the $(m \times n)$ parity-check matrix with $m = n-k$:
- \[{ \boldsymbol{\rm H} } =\left( - { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right) \hspace{0.05cm}.\]
- This equation holds in general, i.e., also in the non-binary case. Since we restrict ourselves to binary codes ⇒ $\mathcal{C} \in \text{GF}(2^n)$ ⇒ $ - \boldsymbol{\rm P} = +\boldsymbol{\rm P}$.
- Thus we obtain the form we will use in the remainder of this chapter.
- \[{ \boldsymbol{\rm H} } =\left( { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right)\hspace{0.05cm}. \]
$\text{Example 8:}$ We continue to consider the example $\text{(5, 3)}$ block code, but now assume the systematic generator matrix $\boldsymbol{\rm G}_{\rm sys}$ that we determined the $\text{Example 5}$:
- \[ \boldsymbol{\rm G_{sys} } = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix} =\left({ \boldsymbol{\rm I} }_3 \: ; \: { \boldsymbol{\rm P} }\right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm I_3} }= \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix}, \hspace{0.3cm} { \boldsymbol{\rm P} }= \begin{pmatrix} 0 &1 \\ 1 &0\\ 0 &0 \end{pmatrix} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} { \boldsymbol{\rm P}^{\rm T} } = \begin{pmatrix} 0 &1 &0\\ 1 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]
- This gives the following for the parity-check matrix
- \[{ \boldsymbol{\rm H} } =\left({ \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_2 \right) = \begin{pmatrix} 0 &1 &0 &1 &0\\ 1 &0 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.\]
- The following code table results:
- \[\underline{u}_0 = (0, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_4 = (1, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_4 = (1, 0, 0, 0, 1) \hspace{0.05cm},\]
- \[\underline{u}_1 = (0, 0, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_1 = (0, 0, 1, 0, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_5 =(1, 0, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_5 = (1, 0, 1, 0, 1)\hspace{0.05cm},\]
- \[\underline{u}_2 =(0, 1, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_6 =(1, 1, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_6 = (1, 1, 0, 1, 1)\hspace{0.05cm},\]
- \[\underline{u}_3 = (0, 1, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_7 = (1, 1, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_7 = (1, 1, 1, 1, 1) \hspace{0.05cm}.\]
- Together with the vector $\underline{x} = (u_1,\ u_2,\ u_3,\ p_1,\ p_2) = (x_1,\ x_2,\ x_3,\ x_4,\ x_5)$ the parity bits are then:
- \[p_1 = u_2 \hspace{0.05cm},\hspace{0.2cm}p_2 = u_1 \hspace{0.05cm},\]
and the corresponding parity-check equations of the decoder:
- \[x_2 + x_4 = 0 \hspace{0.05cm},\hspace{0.2cm}x_1 + x_5 = 0 \hspace{0.05cm}.\]
You can see from these equations and from the above code table:
- This code offers no protection against a transmission error with respect to the third bit $(x_3 = u_3)$ .
- This, of course, does not allow for error detection, and much less error correction.
- But the same is true for the non-systematic code according to $\text{Example 7}$ in the last section.
Representation of SPC and RC as dual codes
For the codes already dealt with in the chapter $\text{Examples of binary block codes}$, the generator matrix $\boldsymbol{\rm G}$ and the parity-check matrix $\boldsymbol{\rm H}$ are to be given in each case. Let the code length always be $n = 5$ for the following examples, but the results can be interpreted in the same way for other code lengths. It applies to
- the $\text{single parity–check code}$ ⇒ $\text{SPC (5, 4)}$:
- \[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.5cm}{ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &0 &1\\ 0 &0 &1 &0 &1\\ 0 &0 &0 &1 &1 \end{pmatrix} \hspace{0.05cm};\]
- the $\text{repetition code}$ ⇒ $\text{RC (5, 1)}$:
- \[{ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.5cm}{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &0 &1\\ 0 &0 &1 &0 &1\\ 0 &0 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.\]
The first equation can be easily derived from the respective definition and the derived equation follows from the relation $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$.
From the above matrices can be generalized:
- The generator matrix of the $\text{RC (5, 1)}$ is identical to the parity-check matrix of the $\text{SPC (5, 4)}$. In each case they are $(5 \times 1)$ matrices.
- The parity-check matrix of the $\text{RC (5, 1)}$ is identical to the generator matrix of the $\text{SPC (5, 4)}$. These two matrices each have $5$ columns and $4$ rows.
- This situation arises because we are dealing here with so-called "dual codes". For explanation we need two more definitions:
$\text{Definition:}$ Two linear codes $\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$, both made of ${\rm GF}(2^n)$, are »orthogonal« if all code words $\underline{x} \in \mathcal{C}$ to all code words $\underline{x}\hspace{0.05cm}' \in \mathcal{C}\hspace{0.05cm}'$ are orthogonal.
- One then refers to $\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$ as »dual codes«.
$\text{Definition:}$ Two code words $\underline{x} \in{\rm GF}(2^n)$ and $\underline{x\hspace{0.05cm}'} \in {\rm GF}(2^n)$ are »orthogonal« to each other whenever the $\text{inner product}$ disappears:
- \[\big \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \big \rangle = \sum_{i=1 }^{n} x_i \cdot x\hspace{0.05cm}'_i = 0 \hspace{0.05cm}, \hspace{0.5cm} \left \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \right \rangle \in {\rm GF}(2^n) \hspace{0.05cm}.\]
Because of the product in ${\rm GF}(2^n)$, the following code word pairs are also orthogonal to each other:
- \[\left \langle \hspace{0.05cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (1, 1, 1, 0) \hspace{0.05cm} \right \rangle = 0\hspace{0.05cm},\hspace{0.8cm} \left \langle \hspace{0.1cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (0, 1, 1, 0) \hspace{0.1cm}\right \rangle = 0\hspace{0.05cm}.\]
- The code $\mathcal{C}$ spans a $k$–dimensional subvector space in ${\rm GF}(2^n)$.
- The subspace of the dual code $\mathcal{C}\hspace{0.05cm}'$ is orthogonal to it and has dimension $n-k$.
- Thus follows: ${\rm dim} \{ \mathcal{C} \} + {\rm dim} \{ \mathcal{C}\hspace{0.05cm}' \} = n\hspace{0.05cm}.$
Some properties of the (7, 4, 3) Hamming code
Let us summarize again the previous results of this chapter using the example of the systematic Hamming code, which has already been described in detail in the chapter $\text{Examples of Binary Block Codes}$ . This $\text{(7, 4, 3)}$ code is characterized by
- the number of parity-check equations $m = 3$,
- the code length $n = 2^m-1 = 7$,
- the information word length $k = n-m = 4$,
- the number of code words (dimension) $2^k =16$ ,
- the rate $R= k/n = 4/7$,
- the minimum distance $d_{\rm min} = 3$ $($independent of $m$, $n$ and $k)$.
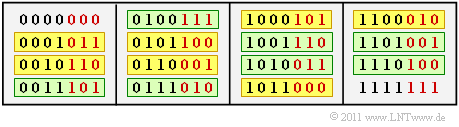
In the above table the $2^4 = 16$ code words are given
(black: four information bits, red: three parity bits).
One can see from this:
- The code includes both the all zero word "$0000000$" and the all one word "$1111111$".
- There are seven code words resulting from "$0001011$" each by cyclic shift (all highlighted in yellow).
- There are seven code words resulting from "$0011101$" each by cyclic shift (all highlighted in green).
- For each code word also exists the "negated" code word, for example, besides "$0001011$" there is also the code word "$1110100$".
- The parity-check matrix can be written as follows:
- \[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}=\left({ \boldsymbol{\rm P}}^{\rm T} \: ; \: { \boldsymbol{\rm I}}_3 \right)\hspace{0.8cm} \Rightarrow\hspace{0.8cm}{ \boldsymbol{\rm P}}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 \\ 0 &1 &1 &1 \\ 1 &1 &0 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.2cm}{ \boldsymbol{\rm I}}_3 = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.05cm}.\]
- Accordingly, the following applies to the generator matrix:
- \[{ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_4 \: ; \: { \boldsymbol{\rm P}}\right)
= \begin{pmatrix}
1 &0 &0 &0 &1 &0 &1\\
0 &1 &0 &0 &1 &1 &1\\
0 &0 &1 &0 &1 &1 &0\\
0 &0 &0 &1 &0 &1 &1
\end{pmatrix}\hspace{0.05cm}.\]
Exercises for the chapter
Exercise 1.7: Check and Generator Matrix of the HC (7, 4, 3)
Exercise 1.7Z: Classification of Block Codes
Exercise 1.8Z: Equivalent Codes
Exercise 1.9: Extended Hamming Code
Exercise 1.9Z: Extension and/or Puncturing
Exercise 1.10: Some Generator Matrices