Difference between revisions of "Aufgaben:Exercise 3.12Z: Ring and Feedback"
From LNTwww
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Distance_Characteristics_and_Error_Probability_Barriers}} |
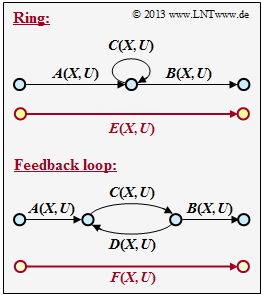
| − | [[File: | + | [[File:EN_KC_Z_3_12.png|right|frame|Ring and feedback in the state transition diagram]] |
| − | + | In order to determine the path weighting enumerator function $T(X)$ of a convolutional code from the state transition diagram, it is necessary to reduce the diagram until it can be represented by a single connection from the initial state to the final state. | |
| − | + | In the course of this diagram reduction can occur: | |
| − | * | + | * serial and parallel transitions, |
| − | |||
| − | |||
| + | * a ring according to the sketch above, | ||
| − | + | * a feedback according to the sketch below. | |
| − | |||
| − | |||
| − | |||
| + | For these two graphs, find the correspondences $E(X, \, U)$ and $F(X, \, U)$ depending on the given functions $A(X, \, U), \ B(X, \ U), \ C(X, \, U), \ D(X, \, U)$ . | ||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <u>Hints:</u> | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds| "Distance Characteristics and Error Probability Bounds"]]. | ||
| + | |||
| + | * This exercise is intended to prove some of the statements on the [[Channel_Coding/Distance_Characteristics_and_Error_Probability_Bounds#Rules_for_manipulating_the_state_transition_diagram|"Rules for manipulating the state transition diagram"]] section. | ||
| + | |||
| + | * Applied these rules in [[Aufgaben:Exercise_3.12:_Path_Weighting_Function|$\text{Exercise 3.12}$]] and [[Aufgaben:Exercise_3.13:_Path_Weighting_Function_again|$\text{Exercise 3.13}$]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the listed transitions are possible with the ring? |
| + | |type="[]"} | ||
| + | + $S_1 → S_2 → S_3$, | ||
| + | + $S_1 → S_2 → S_2 → S_2 → S_3$, | ||
| + | - $S_1 → S_2 → S_1 → S_2 → S_3$. | ||
| + | |||
| + | {What is the substitution $E(X, \, U)$ of a ring? | ||
| + | |type="()"} | ||
| + | - $E(X, \, U) = [A(X, \, U) + B(X, \, U)] \ / \ [1 \, -C(X, \, U)]$, | ||
| + | + $E(X, \, U) = A(X, \, U) \cdot B(X, \, U) \ / \ [1 \, -C(X, \, U)]$, | ||
| + | - $E(X, \, U) = A(X, \, U) \cdot C(X, \, U) \ / \ [1 \, -B(X, \, U)]$. | ||
| + | |||
| + | {Which of the listed transitions are possible with feedback? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + $S_1 → S_2 → S_3 → S_4$, |
| − | - | + | - $S_1 → S_2 → S_3 → S_2 → S_4$, |
| + | + $S_1 → S_2 → S_3 → S_2 → S_3 → S_4$, | ||
| + | + $S_1 → S_2 → S_3 → S_2 → S_3 → S_2 → S_3 → S_4$. | ||
| − | { | + | {What is the substitution $F(X, \, U)$ of a feedback? |
| − | |type=" | + | |type="()"} |
| − | $ | + | + $F(X, \, U) = A(X, \, U) \cdot B(X, \, U) \cdot C(X, \, U) \ / \ [1 \, -C(X, \, U) \cdot D(X, \, U)]$ |
| + | - $F(X, \, U) = A(X, \, U) \cdot B(X, \, U) \ / \ [1 \, -C(X, \, U) + D(X, \, U)]$. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 1 and 2</u>: |
| − | '''(2)''' | + | *In general terms, one first goes from $S_1$ to $S_2$, remains $j$–times in the state $S_2 \ (j = 0, \ 1, \, 2, \ \text{ ...})$, and finally continues from $S_2$ to $S_3$. |
| − | '''(3)''' | + | |
| − | '''(4)''' | + | |
| − | '''( | + | |
| + | '''(2)''' Correct is the <u>solution suggestion 2</u>: | ||
| + | *In accordance with the explanations for subtask '''(1)''', one obtains for the substitution of the ring: | ||
| + | :$$E \hspace{-0.15cm} \ = \ \hspace{-0.15cm} A \cdot B + A \cdot C \cdot B + A \cdot C^2 \cdot B + A \cdot C^3 \cdot B + \text{ ...} \hspace{0.1cm}=A \cdot B \cdot [1 + C + C^2+ C^3 +\text{ ...}\hspace{0.1cm}] | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The parenthesis expression gives $1/(1 \, –C)$. | ||
| + | :$$E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Correct are the <u>solutions 1, 3 and 4</u>: | ||
| + | * One goes first from $S_1$ to $S_2 \ \Rightarrow \ A(X, \, U)$, | ||
| + | |||
| + | * then from $S_2$ to $S_3 \ \Rightarrow \ C(X, \, U)$, | ||
| + | |||
| + | * then $j$–times back to $S_2$ and again to $S_3 \ (j = 0, \ 1, \ 2, \ \text{ ...} \ ) \ \Rightarrow \ E(X, \, U)$, | ||
| + | |||
| + | * finally from $S_3$ to $S_4 \ \Rightarrow \ B(X, \, U)$, | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Thus, the correct solution is the <u>suggested solution 1</u>: | ||
| + | *According to the sample solution to subtask '''(3)''' applies: | ||
| + | :$$F(X, U) = A(X, U) \cdot C(X, U) \cdot E(X, U) \cdot B(X, U)\hspace{0.05cm}$$ | ||
| + | |||
| + | *Here $E(X, \, U)$ describes the path "$j$–times" back to $S_2$ and again to $S_3 \ (j =0, \ 1, \ 2, \ \text{ ...})$: | ||
| + | :$$E(X, U) = 1 + D \cdot C + (1 + D)^2 + (1 + D)^3 + \text{ ...} \hspace{0.1cm}= \frac{1}{1-C \hspace{0.05cm} D} | ||
| + | \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U) \cdot D(X, U)} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^3.5 Distance Properties^]] |
Latest revision as of 17:27, 22 November 2022
In order to determine the path weighting enumerator function $T(X)$ of a convolutional code from the state transition diagram, it is necessary to reduce the diagram until it can be represented by a single connection from the initial state to the final state.
In the course of this diagram reduction can occur:
- serial and parallel transitions,
- a ring according to the sketch above,
- a feedback according to the sketch below.
For these two graphs, find the correspondences $E(X, \, U)$ and $F(X, \, U)$ depending on the given functions $A(X, \, U), \ B(X, \ U), \ C(X, \, U), \ D(X, \, U)$ .
Hints:
- This exercise belongs to the chapter "Distance Characteristics and Error Probability Bounds".
- This exercise is intended to prove some of the statements on the "Rules for manipulating the state transition diagram" section.
- Applied these rules in $\text{Exercise 3.12}$ and $\text{Exercise 3.13}$.
Questions
Solution
(1) Correct are the solutions 1 and 2:
- In general terms, one first goes from $S_1$ to $S_2$, remains $j$–times in the state $S_2 \ (j = 0, \ 1, \, 2, \ \text{ ...})$, and finally continues from $S_2$ to $S_3$.
(2) Correct is the solution suggestion 2:
- In accordance with the explanations for subtask (1), one obtains for the substitution of the ring:
- $$E \hspace{-0.15cm} \ = \ \hspace{-0.15cm} A \cdot B + A \cdot C \cdot B + A \cdot C^2 \cdot B + A \cdot C^3 \cdot B + \text{ ...} \hspace{0.1cm}=A \cdot B \cdot [1 + C + C^2+ C^3 +\text{ ...}\hspace{0.1cm}] \hspace{0.05cm}.$$
- The parenthesis expression gives $1/(1 \, –C)$.
- $$E(X, U) = \frac{A(X, U) \cdot B(X, U)}{1- C(X, U)} \hspace{0.05cm}.$$
(3) Correct are the solutions 1, 3 and 4:
- One goes first from $S_1$ to $S_2 \ \Rightarrow \ A(X, \, U)$,
- then from $S_2$ to $S_3 \ \Rightarrow \ C(X, \, U)$,
- then $j$–times back to $S_2$ and again to $S_3 \ (j = 0, \ 1, \ 2, \ \text{ ...} \ ) \ \Rightarrow \ E(X, \, U)$,
- finally from $S_3$ to $S_4 \ \Rightarrow \ B(X, \, U)$,
(4) Thus, the correct solution is the suggested solution 1:
- According to the sample solution to subtask (3) applies:
- $$F(X, U) = A(X, U) \cdot C(X, U) \cdot E(X, U) \cdot B(X, U)\hspace{0.05cm}$$
- Here $E(X, \, U)$ describes the path "$j$–times" back to $S_2$ and again to $S_3 \ (j =0, \ 1, \ 2, \ \text{ ...})$:
- $$E(X, U) = 1 + D \cdot C + (1 + D)^2 + (1 + D)^3 + \text{ ...} \hspace{0.1cm}= \frac{1}{1-C \hspace{0.05cm} D} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} F(X, U) = \frac{A(X, U) \cdot B(X, U)\cdot C(X, U)}{1- C(X, U) \cdot D(X, U)} \hspace{0.05cm}.$$