Difference between revisions of "Aufgaben:Exercise 4.7: Product Code Decoding"
From LNTwww
| Line 43: | Line 43: | ||
*The corrected code word is then $\underline{y} + \underline{e}_{\mu}$. | *The corrected code word is then $\underline{y} + \underline{e}_{\mu}$. | ||
| − | [[File: | + | [[File:EN_KC_A_4_7_Zusatz.png|right|frame|Predefined encoder and receiver matrices]] |
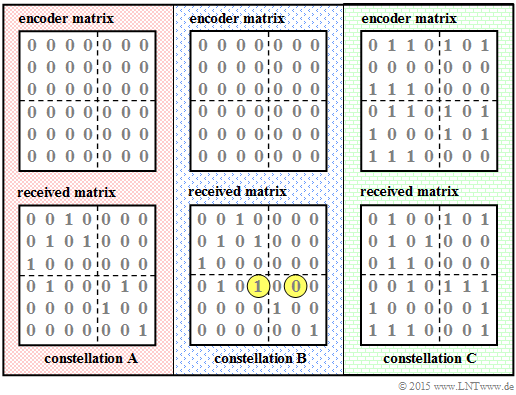
<br><br><br>The accompanying diagram shows three different encoder– and receiver matrices to be analyzed in the subtasks '''(1)''', '''(2)''', and '''(3)''': | <br><br><br>The accompanying diagram shows three different encoder– and receiver matrices to be analyzed in the subtasks '''(1)''', '''(2)''', and '''(3)''': | ||
*We name them constellation $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$. | *We name them constellation $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$. | ||
Revision as of 17:44, 7 December 2022
Syndrome tables of the considered component codes $\mathcal{C}_1$ and $\mathcal{C}_2$
We consider, as in the "Exercise 4.6" a product code based on.
- the Hamming code $\rm HC \ (7, \ 4, \ 3)$ ⇒ $\mathcal{C}_1$,
- the truncated Hamming code $\rm HC \ (6, \ 3, \ 3)$ ⇒ $\mathcal{C}_2$.
The parity-check matrices of these component codes are:
- $${ \boldsymbol{\rm H}}_1 = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &1 &0 \\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm H}}_2 = \begin{pmatrix} 1 &1 &0 &1 &0 &0 \\ 1 &0 &1 &0 &1 &0 \\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
For the sake of completeness, the generator matrices are also given, but they are not needed to solve the exercise:
- $${ \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1 \\ 0 &1 &0 &0 &1 &1 &0 \\ 0 &0 &1 &0 &0 &1 &1 \\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm G}}_2 = \begin{pmatrix} 1 &0 &0 &1 &1 &0 \\ 0 &1 &0 &1 &0 &1 \\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$
The Hard Decision Decoding of this code is preferably done iteratively, by alternately syndromdecoding all rows and then all columns. See: "Iterative Syndrome Decoding of Product Codes".
Syndrome decoding of (one-dimensional) block codes has already been covered in the chapter "Decoding of Linear Block Codes" . Here is a brief summary and an adaptation to the two-dimensional case:
- From the received word $\underline{y}$ (a row or a column of the given received matrix), the syndrome corresponding to $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$ respectively $\underline{s} = \underline{y} \cdot \mathbf{H}_2^{\rm T}$ formed.
- With the result $\underline{s} = \underline{s}_{\mu}$ one can read in above tables the so called side class adder $\underline{e}_{\mu}$ .
- The corrected code word is then $\underline{y} + \underline{e}_{\mu}$.
Predefined encoder and receiver matrices
The accompanying diagram shows three different encoder– and receiver matrices to be analyzed in the subtasks (1), (2), and (3):
- We name them constellation $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$.
- Marked in yellow are the differences in the reception matrix of constellation $\mathbf{B}$ versus $\mathbf{A}$.
- In both cases, the code matrix consists only of zeros.
- The code matrix of $\rm C$ was determined in the Aufgabe 4.6 .
Hints:
- This exercise belongs to the chapter "Basics of Product Codes".
- Reference is made in particular to the page "Iterative syndrome decoding of product codes".
Questions
Solution
(1) The decoding process of the receive matrix $\mathbf{A}$ is illustrated by the following diagram.
Syndrome decoding of the two-dimensional received matrix $\mathbf{A}$.
- The single errors in rows 1, 3, 5 and 6 are detected by $(7, \ 4, \ 3)$–Hamming code and can be corrected
⇒ green markings in the graphic "1st iteration horizontal". - For the second row results the syndrome
- $$\underline{s} = \underline{y}_2 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 \\ 1 &1 &0 \\ 0 &1 &1 \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1 \hspace{0.03cm}.$$
- According to the upper syndrome table on the information page, the last bit is thus incorrectly "corrected". Incorrect corrections are entered in red in the upper graphic.
- Correspondingly applies to the fourth row:
- $$\underline{s} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0 \right ) \cdot { \boldsymbol{\rm H}}_1^{\rm T} = \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right )= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \underline{s}_4 \hspace{0.05cm}.$$
- This causes a miscorrection of bit 5.
- Vertical decoding of columns 1, 3, 4, 5, 6, and 7 is straightforward because there is at most one error per column, which can be corrected by the truncated Hamming code $\rm (6, \ 3, \ 3)$.
- In column 2, however, there is a miscorrection of the last bit according to the lower syndrome table. With the transpose of the $\rm (6, \ 3, \ 3)$ parity-check matrix $\mathbf{H}_2$ results namely:
- $$\underline{s}= \underline{y}_{2{\rm S}}\cdot { \boldsymbol{\rm H}}_2^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \begin{pmatrix} 1 &1 &0 \\ 1 &0 &1 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) + \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1.$$
- The second horizontal decoding is problem-free, since now at most one error occurs in each row ⇒ Solution suggestion 3.
(2) The following graphic shows the decoding process according to the specifications given by $\mathbf{B}$.
For syndrome decoding of the two-dimensional receive matrix $\mathbf{B}$.
Despite only minor modifications compared to $\mathbf{A}$, there are now serious differences:
- Due to the first horizontal decoding, the "corrected" rows 2 and 4 now read equally: $(0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1)$, i.e., the last bit of these rows is miscorrected in each case.
- Vertical decoding results in identical columns 2, 4, and 6, namely $(0, \, 1, \, 0, \, 1, \, 0, \, 1)$. After that, there are three ones (or none) in each row and in each column.
- This constellation remains for arbitrary further (horizontal or vertical) decodings, because for $d_{\rm min} = 3$ always the syndrome $\underline{s}_0 = (0, \, 0, \, 0)$ results.
The correct solution is proposal 5.
(3) Comparing the encoder– and receiver matrices (differences are marked in blue), one can create the error matrix by modulo 2 additions according to the following graph.
Matrix representation of encoder, receiver and error pattern
The error matrix is equal to the receive matrix of $\mathbf{A}$ ⇒ again, proposed solution 3 is correct.
