Difference between revisions of "Channel Coding/Error Probability and Application Areas"
| (48 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü=Reed–Solomon–Codes | + | |Untermenü=Reed–Solomon–Codes and Their Decoding |
| − | |Vorherige Seite= | + | |Vorherige Seite=Error Correction According to Reed-Solomon Coding |
| − | |Nächste Seite= | + | |Nächste Seite=Basics of Convolutional Coding |
}} | }} | ||
| − | == | + | == Block error probability for RSC and BDD == |
<br> | <br> | ||
| − | + | For error probability calculation we start from the same block diagram as in chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding| "Error Correction According to Reed-Solomon Coding"]], but here we choose the code word estimator $(\underline {y} → \underline {z})$ to [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Bounded_Distance_Decoding_Procedure| $\text{Bounded Distance Decoding}$]] $\rm (BDD)$. For "Maximum Likelihood Decoding" the results are slightly better.<br> | |
| − | [[File: | + | [[File:EN_KC_T_2_6_S1.png|right|frame|System model with Reed–Solomon coding, $m$ BSC and ''Bounded Distance Decoding''|class=fit]] |
| − | + | Let the block error probability be defined as follows: | |
| − | ::<math>{ \rm Pr( | + | ::<math>{ \rm Pr(block\:error)} = { \rm Pr}( \underline{v} \ne \underline{u})= { \rm Pr}( \underline{z} \ne \underline{c}) = { \rm Pr}( f >t) \hspace{0.05cm}.</math> |
| − | + | Due to the BDD assumption, the same simple result is obtained as for the binary block codes, namely the probability that | |
| + | *the number $f$ of errors in the block $($received word$)$ | ||
| − | ::<math>{\rm Pr( | + | *is greater than the correctability $t$ of the code. |
| + | |||
| + | |||
| + | Since for the random variable $f$ $($number of errors in the block$)$ there is a [[Theory_of_Stochastic_Signals/Binomial_Distribution#Probabilities_of_the_binomial_distribution| $\text{binomial distribution}$]] in the range $0 ≤ f ≤ n$ we obtain: | ||
| + | |||
| + | ::<math>{\rm Pr(block\:error)} = | ||
\sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.</math> | \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.</math> | ||
| − | + | *But while in the first main chapter $c_i ∈ \rm GF(2)$ has always been applied and thus the $f$ transmission errors were in each case »'''bit errors'''«, | |
| − | |||
| − | * | + | *under Reed–Solomon coding a transmission error $(y_i \ne c_i)$ is always understood to be a »'''symbol error'''« because of $c_i ∈ {\rm GF}(2^m)$ as well as $y_i ∈ {\rm GF}(2^m)$. |
| + | |||
| + | |||
| + | This results in the following differences: | ||
| + | # The discrete channel model used to describe the binary block codes is the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC| $\text{Binary Symmetric Channel}$]] $\rm (BSC)$. Each bit $c_i$ of a code word is falsified $(y_i \ne c_i)$ with probability $\varepsilon$ and correctly transmitted $(y_i = c_i)$ with probability $1-\varepsilon$.<br> | ||
| + | # For Reed–Solomon coding, one must replace the "1–BSC" model with the "''m''–BSC" model. A symbol $c_i$ is falsified with probability $\varepsilon_{\rm S}$ into another symbol $y_i$ $($no matter which one$)$ and arrives with probability $1-\varepsilon_{\rm S}$ unfalsified at the receiver.<br><br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | We start from the BSC parameter $\varepsilon = 0.1$ and consider Reed–Solomon code symbols $c_i ∈ {\rm GF}(2^8)$ ⇒ $m = 8$, $q = 256$, $n = 255$. | |
| − | + | *For a symbol falsification $(y_i \ne c_i)$ already one wrong bit is sufficient. | |
| + | |||
| + | *Or expressed differently: If $y_i = c_i$ is to be valid, then all $m = 8$ bits of the code symbol must be transmitted correctly: | ||
::<math>1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 | ::<math>1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | * | + | *Thus, for the "8–BSC" model, the falsification probability $\varepsilon_{\rm S} ≈ 0.57$. |
| − | * | + | |
| − | :$${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta = 0.57/255 ≈ 0.223\%.$$}}<br> | + | *With the further assumption that the falsification of $c_i = \beta$ into any other symbol $y_i = \gamma \ne \beta$ is equally likely, we obtain: |
| + | :$${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta) = 0.57/255 ≈ 0.223\%.$$}}<br> | ||
| − | == | + | == Application of Reed–Solomon coding for binary channels == |
<br> | <br> | ||
| − | + | The prerequisites for the following calculation of block error probability of a Reed–Solomon coding system and conversion to binary symbols are summarized in the diagram: | |
| − | + | [[File:EN_KC_T_2_6_S2a_neu_v3.png|right|frame|Application of Reed-Solomon coding for binary channels. at point<br>'''(1)''' $k$–bit symbols; '''(2)''' $n$–bit symbols; '''(3)''' $n$–bit symbols; '''(4)''' $(n \cdot m)$–bit blocks;|class=fit]] | |
| − | + | # Assume $(n,\ k)$ Reed–Solomon coding with symbols of $c_i ∈ {\rm GF}(2^m)$. The smaller the code rate $R=k/n$, the less information can be transmitted at a fixed data rate.<br> | |
| + | # Each symbol is represented by $m$ bits ⇒ "binary mapping". A block $($code word $\underline {c} )$ thus consists of $n$ symbols or of $n \cdot m$ binary characters $($bits$)$ combined in $\underline {c}_{\rm bin} $.<br> | ||
| + | # In addition, the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_binary_input|$\text{AWGN Channel}$]], identified by the parameter $E_{\rm B}/N_0 $ is assumed. According to this channel model the transmission is bipolar: "0" ↔ $+1$ and "1" ↔ $-1$. | ||
| + | # The receiver makes hard decisions on bit level. Before decoding including error correction, the binary symbols are converted back to ${\rm GF}(2^m)$ symbols.<br> | ||
| − | |||
| − | + | The "Bounded Distance Decoding" equation from the last section is based on the "''m''–BSC" model: | |
| − | + | ::<math>{\rm Pr(block\:error)} = | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ::<math>{\rm Pr( | ||
\sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},</math> | \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},</math> | ||
| − | + | Starting from the AWGN–channel ("Additive White Gaussian Noise"), one comes | |
| − | * | + | *with the [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Exceedance_probability|$\text{complementary Gaussian error function}$]] ${\rm Q}(x)$ to the »'''bit error probability'''« ⇒ "1–BSC" parameter: |
::<math>\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) | ::<math>\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) | ||
| Line 65: | Line 74: | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | * | + | *and from this to the »'''symbol error probability'''« ⇒ "''m''–BSC" parameter: |
::<math>\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m | ::<math>\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m | ||
| Line 71: | Line 80: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ One gets with |
| + | # the code rate $R=k/n = 239/255 = 0.9373$, | ||
| + | # the AWGN parameter $10 \cdot \lg \ E_{\rm B}/N_0 = 7 \, \rm dB$ ⇒ $E_{\rm B}/N_0 ≈ 5$, and | ||
| + | # eight bits per symbol ⇒ $m = 8$, | ||
| + | # the code length $n = 2^8-1 = 255$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | the following numerical values for | |
| + | *the parameter $\varepsilon$ of the "1–BSC" model ⇒ "bit error probability": | ||
| − | + | :$$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot 0.9373 \cdot 5} \big ) = {\rm Q} \big (3.06\big ) \approx 1.1 \cdot 10^{-3}=0.11 \%$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | *the parameter $\varepsilon_{\rm S}$ of the "8–BSC" model ⇒ "symbol error probability" or "block error probability": |
| − | |||
| + | :$$\varepsilon_{\rm S} = 1 - (1 - 1.1 \cdot 10^{-3})^8 = 1 - 0.9989^8 = 1 - 0.9912 \approx 0.88 \% | ||
| + | \hspace{0.2cm}(\approx 8 \cdot \varepsilon)\hspace{0.05cm}.$$ | ||
| − | + | ⇒ So every single symbol is transmitted with more than $99$ percent probability without errors.}}<br> | |
| − | |||
| − | |||
| − | : | + | == BER of Reed–Solomon coding for binary channels == |
| − | + | <br> | |
| + | The following graph shows the block error probabilities given in [Liv10]<ref name='Liv10'>Liva, G.: Channel Coding. Lecture Notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010.</ref> as a function of the AWGN quotient $10 \cdot \lg \ E_{\rm B}/N_0$. | ||
| + | |||
| + | Shown are the calculated curves ${ \rm Pr}( \underline{v} \ne \underline{u})$ for two different Reed–Solomon codes corresponding to the "Deep Space Standards" according to $\rm CCSDS$ $($"Consultative Committee for Space Data Systems"$)$, namely | ||
| + | [[File:EN_KC_T_2_6_S2b.png|right|frame|Block error probabilities of two Reed-Solomon codes of length $n = 255$ <br><u>Note:</u> You are to perform completely the calculation in the [[Aufgaben:Exercise_2.15:_Block_Error_Probability_with_AWGN|"Exercise 2.15"]] for the $\text{RSC (7, 3, 5)}_{8}$ – thus for somewhat clearer parameters.|class=fit]] | ||
| − | + | # the $\text{RSC (255, 239, 17)}_{256}$ with code rate $R=0.9373$, which can correct up to $t = 8$ errors, and<br> | |
| + | # the $\text{RSC (255, 223, 33)}_{256}$ with higher correction capability $(t = 16)$ due to smaller code rate. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We analyze the point highlighted in yellow in the graph, valid for | |
| + | *the $\text{RSC (255, 239, 17)}_{256}$, and | ||
| − | + | *$10 \cdot \lg \ E_{\rm B}/N_0 = 7.1 \,\rm dB$ ⇒ $\varepsilon = 0.007$. | |
| − | * | ||
| − | |||
| − | + | The corresponding block error probability results according to the diagram to | |
| + | ::<math>{\rm Pr(block\:error)} = | ||
| + | \sum_{f =9}^{255} {255 \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{255-f}\approx 10^{-4} \hspace{0.05cm}.</math> | ||
| − | + | Dominant here is the first term $($for $f=9)$, which already accounts for $\approx 80\%$ : | |
| − | $ | ||
| − | |||
| − | + | :$${255 \choose 9} \approx 1.1 \cdot 10^{16}\hspace{0.05cm},\hspace{0.15cm} | |
| − | + | \varepsilon_{\rm S}^9 \approx 4 \cdot 10^{-20}\hspace{0.05cm},\hspace{0.15cm} | |
| − | + | (1 -\varepsilon_{\rm S})^{246} \approx 0.18$$ | |
| − | + | ::$$ \Rightarrow \hspace{0.15cm} {\rm Pr}(f = 9) \approx 8 \cdot 10^{-5} | |
| − | + | \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| + | This should be taken as proof that one may stop the summation already after a few terms.<br> | ||
| − | + | The results shown in the graph can be summarized as follows: | |
| + | # For small $E_{\rm B}/N_0$ $($of the AWGN channel$)$, the Reed–Solomon codes are completely unsuitable. | ||
| + | # Both codes are for $10 \cdot \lg \ E_{\rm B}/N_0 < 6 \,\rm dB$ above the $($black$)$ comparison curve for uncoded transmission.<br> | ||
| + | # The $\text{RSC (255, 223, 33)}_{256}$ calculation differs only in the lower summation limit $(f_{\rm min} = 17)$ and by a slightly larger $\varepsilon_{\rm S}$ $($because $R = 0.8745)$.<br> | ||
| + | # For $\rm BER = 10^{-6}$, this "red code" $($with $t = 16)$ is better only by about $1 \, \rm dB$ than the "green code" $($with $t = 8)$. | ||
| + | # So the results of both codes are rather disappointing.<br> | ||
| − | |||
| − | {{ | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{Conclusion:}$ |
| + | *Reed–Solomon codes are not very good at the memoryless AWGN channel. Both codes are more than $4 \, \rm dB$ away from the information-theoretical [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding#AWGN_channel_capacity_for_binary_input_signals| $\text{Shannon bound }$ ]].<br> | ||
| − | [[ | + | *But Reed–Solomon codes are very effective with so-called [[Digital_Signal_Transmission/Burst_Error_Channels| $\text{Burst Error Channels}$]]. They are therefore mainly used for fading channels, memory systems, etc.<br> |
| − | + | *Reed–Solomon codes are not perfect. The consequences of this are covered in [[Aufgaben:Exercise_2.16:_Bounded_Distance_Decoding:_Decision_Regions|"Exercise 2.16"]].}}<br> | |
| − | |||
| − | + | == Typical applications with Reed–Solomon coding== | |
| − | + | <br> | |
| − | + | Reed–Solomon coding is often applied according to the diagram together with an "inner code" in cascaded form. | |
| + | [[File:EN_KC_T_2_6_S3.png|right|frame|Code scheme with cascading|class=fit]] | ||
| + | *The inner code is almost always a binary code and in satellite– and mobile communications often a convolutional code. | ||
| + | |||
| + | *If one wishes to study only Reed–Solomon encoding/decoding, one replaces the grayed components in a simulation with a single block called a "super channel".<br> | ||
| + | *Concatenated coding systems are very efficient if an interleaver is connected between the two encoders to further relax burst errors.<br> | ||
| + | <br clear=all> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ The diagram shows an example of such an interleaver, where we restrict ourselves to a $20 × 4$ matrix. In practice, these matrices are significantly larger.<br> |
| − | |||
| − | + | [[File:EN_KC_T_2_6_S4_neu.png|right|frame|Interleaver matrix for $20 × 4$ symbols|class=fit]] | |
| − | + | The interleaver is written row–by–row and read out column–by–column $($blue label$)$. With the de–interleaver $($green label$)$ the sequence is exactly the other way round. | |
| − | * | + | *The Reed–Solomon symbols are therefore not forwarded to the inner coder consecutively, but according to the specified sequence as symbol '''1, 21, 41, 61, 2, 22,''' etc. .<br> |
| − | * | + | *A contiguous area $($here the symbols '''42, 62, 3, 23, 43, 63, 4, 24''' ⇒ around the rectangle outlined in red below$)$ is destroyed on the channel, for example by a scratch on the channel "storage medium".<br> |
| − | * | + | *After de–interleaving, the symbol sequence is again '''1, 2, 3,''' ... <br>You can see from the red outlined circles that now this burst error has been largely "broken up".}} |
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Example 4:}$ A very widely used application of Reed–Solomon coding – and also the most commercially successful – is the »'''Compact Disc'''« $\rm (CD)$, whose error correction mechanism has already been described in the [[Channel_Coding/Objective_of_Channel_Coding#Some_introductory_examples_of_error_correction| "introduction chapter"]] $($Example 7$)$ of this book. Here the inner code is also a Reed–Solomon code, and the concatenated coding system can be described as follows: | ||
| + | # Both channels of the stereo–audio signal are sampled at $\text{44.1 kHz}$ each and every sample is digitally represented at $32$ bits $($four bytes$)$.<br> | ||
| + | # The grouping of six samples results in a frame $(192$ Bit$)$ and thus $24$ code symbols from the Galois field $\rm GF(2^8)$. Each code symbol thus corresponds to exactly one byte.<br> | ||
| + | # The first Reed–Solomon code with rate $R_1 = 24/28$ returns $28$ bytes, which are fed to an interleaver of size $28 × 109$ bytes. The readout is done (complicated) diagonally.<br> | ||
| + | # The interleaver distributes contiguous bytes over a large area of the entire disc. This resolves so-called "bursts" e.g. caused by scratches on the $\rm CD$.<br> | ||
| + | # Together with the second Reed–Solomon code $($rate $R_2 = 28/32)$ gives a total rate of $R = (24/28) · (28/32) = 3/4$. Both codes can each correct $t = 2$ symbol errors.<br> | ||
| + | # The two component codes $\text{RSC (28, 24, 5)}$ and $\text{RSC (32, 28, 5)}$ are each based on the Galois field $\rm GF(2^8)$, which would actually mean a code length of $n = 255$ .<br> | ||
| + | #The shorter component codes needed here result from the $\text{RSC (255, 251, 5)}_{256}$ by "shortening" ⇒ see [[Aufgaben:Exercise_1.09Z:_Extension_and/or_Puncturing|"Exercise 1.9Z"]]. However, this measure does not change the minimum distance $d_{\rm min}= 5$ .<br> | ||
| + | # With the subsequent [https://en.wikipedia.org/wiki/Eight-to-fourteen_modulation $\text{Eight to Fourteen Modulation}$] and further control symbols, one finally arrives at the final code rate $ R = 192/588 ≈ 0.326$ of the CD data compression.<br><br> | ||
| − | + | In the section [[Channel_Coding/Objective_of_Channel_Coding#The_.22Slit_CD.22_-_a_demonstration_by_the_LNT_of_TUM | "Slit CD"]] you can see for yourself the correction capabilities of this "cross–interleaved Reed–Solomon coding" with the help of an audio example, but you will also see its limitations}}.<br> | |
| − | == | + | == Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.15:_Block_Error_Probability_with_AWGN|Exercise 2.15: Block Error Probability with AWGN]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.15Z:_Block_Error_Probability_once_more|Exercise 2.15Z: Block Error Probability once more]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_2.16:_Bounded_Distance_Decoding:_Decision_Regions|Exercise 2.16: Bounded Distance Decoding: Decision Regions]] |
| − | == | + | ==References== |
<references/> | <references/> | ||
{{Display}} | {{Display}} | ||
Latest revision as of 14:51, 13 December 2022
Contents
Block error probability for RSC and BDD
For error probability calculation we start from the same block diagram as in chapter "Error Correction According to Reed-Solomon Coding", but here we choose the code word estimator $(\underline {y} → \underline {z})$ to $\text{Bounded Distance Decoding}$ $\rm (BDD)$. For "Maximum Likelihood Decoding" the results are slightly better.
Let the block error probability be defined as follows:
- \[{ \rm Pr(block\:error)} = { \rm Pr}( \underline{v} \ne \underline{u})= { \rm Pr}( \underline{z} \ne \underline{c}) = { \rm Pr}( f >t) \hspace{0.05cm}.\]
Due to the BDD assumption, the same simple result is obtained as for the binary block codes, namely the probability that
- the number $f$ of errors in the block $($received word$)$
- is greater than the correctability $t$ of the code.
Since for the random variable $f$ $($number of errors in the block$)$ there is a $\text{binomial distribution}$ in the range $0 ≤ f ≤ n$ we obtain:
- \[{\rm Pr(block\:error)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.\]
- But while in the first main chapter $c_i ∈ \rm GF(2)$ has always been applied and thus the $f$ transmission errors were in each case »bit errors«,
- under Reed–Solomon coding a transmission error $(y_i \ne c_i)$ is always understood to be a »symbol error« because of $c_i ∈ {\rm GF}(2^m)$ as well as $y_i ∈ {\rm GF}(2^m)$.
This results in the following differences:
- The discrete channel model used to describe the binary block codes is the $\text{Binary Symmetric Channel}$ $\rm (BSC)$. Each bit $c_i$ of a code word is falsified $(y_i \ne c_i)$ with probability $\varepsilon$ and correctly transmitted $(y_i = c_i)$ with probability $1-\varepsilon$.
- For Reed–Solomon coding, one must replace the "1–BSC" model with the "m–BSC" model. A symbol $c_i$ is falsified with probability $\varepsilon_{\rm S}$ into another symbol $y_i$ $($no matter which one$)$ and arrives with probability $1-\varepsilon_{\rm S}$ unfalsified at the receiver.
$\text{Example 1:}$ We start from the BSC parameter $\varepsilon = 0.1$ and consider Reed–Solomon code symbols $c_i ∈ {\rm GF}(2^8)$ ⇒ $m = 8$, $q = 256$, $n = 255$.
- For a symbol falsification $(y_i \ne c_i)$ already one wrong bit is sufficient.
- Or expressed differently: If $y_i = c_i$ is to be valid, then all $m = 8$ bits of the code symbol must be transmitted correctly:
- \[1 - \varepsilon_{\rm S} = (1 - \varepsilon)^m = 0.9^8 \approx 0.43 \hspace{0.05cm}.\]
- Thus, for the "8–BSC" model, the falsification probability $\varepsilon_{\rm S} ≈ 0.57$.
- With the further assumption that the falsification of $c_i = \beta$ into any other symbol $y_i = \gamma \ne \beta$ is equally likely, we obtain:
- $${\rm Pr}(y_i = \gamma\hspace{0.05cm}\vert \hspace{0.05cm}c_i = \beta) = 0.57/255 ≈ 0.223\%.$$
Application of Reed–Solomon coding for binary channels
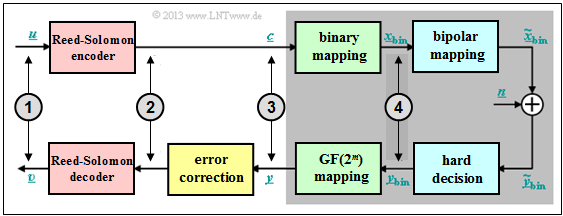
The prerequisites for the following calculation of block error probability of a Reed–Solomon coding system and conversion to binary symbols are summarized in the diagram:
- Assume $(n,\ k)$ Reed–Solomon coding with symbols of $c_i ∈ {\rm GF}(2^m)$. The smaller the code rate $R=k/n$, the less information can be transmitted at a fixed data rate.
- Each symbol is represented by $m$ bits ⇒ "binary mapping". A block $($code word $\underline {c} )$ thus consists of $n$ symbols or of $n \cdot m$ binary characters $($bits$)$ combined in $\underline {c}_{\rm bin} $.
- In addition, the $\text{AWGN Channel}$, identified by the parameter $E_{\rm B}/N_0 $ is assumed. According to this channel model the transmission is bipolar: "0" ↔ $+1$ and "1" ↔ $-1$.
- The receiver makes hard decisions on bit level. Before decoding including error correction, the binary symbols are converted back to ${\rm GF}(2^m)$ symbols.
The "Bounded Distance Decoding" equation from the last section is based on the "m–BSC" model:
- \[{\rm Pr(block\:error)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm},\]
Starting from the AWGN–channel ("Additive White Gaussian Noise"), one comes
- with the $\text{complementary Gaussian error function}$ ${\rm Q}(x)$ to the »bit error probability« ⇒ "1–BSC" parameter:
- \[\varepsilon = {\rm Q} \big (\sqrt{2 \cdot E_{\rm S}/N_0} \big ) = {\rm Q} \big (\sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \big ) \hspace{0.05cm},\]
- and from this to the »symbol error probability« ⇒ "m–BSC" parameter:
- \[\varepsilon_{\rm S} = 1 - (1 - \varepsilon)^m \hspace{0.05cm}.\]
$\text{Example 2:}$ One gets with
- the code rate $R=k/n = 239/255 = 0.9373$,
- the AWGN parameter $10 \cdot \lg \ E_{\rm B}/N_0 = 7 \, \rm dB$ ⇒ $E_{\rm B}/N_0 ≈ 5$, and
- eight bits per symbol ⇒ $m = 8$,
- the code length $n = 2^8-1 = 255$
the following numerical values for
- the parameter $\varepsilon$ of the "1–BSC" model ⇒ "bit error probability":
- $$\varepsilon = {\rm Q} \big (\sqrt{2 \cdot 0.9373 \cdot 5} \big ) = {\rm Q} \big (3.06\big ) \approx 1.1 \cdot 10^{-3}=0.11 \%$$
- the parameter $\varepsilon_{\rm S}$ of the "8–BSC" model ⇒ "symbol error probability" or "block error probability":
- $$\varepsilon_{\rm S} = 1 - (1 - 1.1 \cdot 10^{-3})^8 = 1 - 0.9989^8 = 1 - 0.9912 \approx 0.88 \% \hspace{0.2cm}(\approx 8 \cdot \varepsilon)\hspace{0.05cm}.$$
⇒ So every single symbol is transmitted with more than $99$ percent probability without errors.
BER of Reed–Solomon coding for binary channels
The following graph shows the block error probabilities given in [Liv10][1] as a function of the AWGN quotient $10 \cdot \lg \ E_{\rm B}/N_0$.
Shown are the calculated curves ${ \rm Pr}( \underline{v} \ne \underline{u})$ for two different Reed–Solomon codes corresponding to the "Deep Space Standards" according to $\rm CCSDS$ $($"Consultative Committee for Space Data Systems"$)$, namely
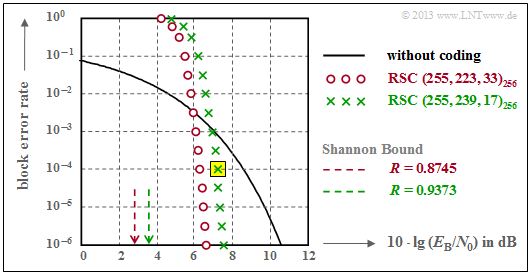
Note: You are to perform completely the calculation in the "Exercise 2.15" for the $\text{RSC (7, 3, 5)}_{8}$ – thus for somewhat clearer parameters.
- the $\text{RSC (255, 239, 17)}_{256}$ with code rate $R=0.9373$, which can correct up to $t = 8$ errors, and
- the $\text{RSC (255, 223, 33)}_{256}$ with higher correction capability $(t = 16)$ due to smaller code rate.
We analyze the point highlighted in yellow in the graph, valid for
- the $\text{RSC (255, 239, 17)}_{256}$, and
- $10 \cdot \lg \ E_{\rm B}/N_0 = 7.1 \,\rm dB$ ⇒ $\varepsilon = 0.007$.
The corresponding block error probability results according to the diagram to
- \[{\rm Pr(block\:error)} = \sum_{f =9}^{255} {255 \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{255-f}\approx 10^{-4} \hspace{0.05cm}.\]
Dominant here is the first term $($for $f=9)$, which already accounts for $\approx 80\%$ :
- $${255 \choose 9} \approx 1.1 \cdot 10^{16}\hspace{0.05cm},\hspace{0.15cm}
\varepsilon_{\rm S}^9 \approx 4 \cdot 10^{-20}\hspace{0.05cm},\hspace{0.15cm}
(1 -\varepsilon_{\rm S})^{246} \approx 0.18$$
- $$ \Rightarrow \hspace{0.15cm} {\rm Pr}(f = 9) \approx 8 \cdot 10^{-5} \hspace{0.05cm}.$$
This should be taken as proof that one may stop the summation already after a few terms.
The results shown in the graph can be summarized as follows:
- For small $E_{\rm B}/N_0$ $($of the AWGN channel$)$, the Reed–Solomon codes are completely unsuitable.
- Both codes are for $10 \cdot \lg \ E_{\rm B}/N_0 < 6 \,\rm dB$ above the $($black$)$ comparison curve for uncoded transmission.
- The $\text{RSC (255, 223, 33)}_{256}$ calculation differs only in the lower summation limit $(f_{\rm min} = 17)$ and by a slightly larger $\varepsilon_{\rm S}$ $($because $R = 0.8745)$.
- For $\rm BER = 10^{-6}$, this "red code" $($with $t = 16)$ is better only by about $1 \, \rm dB$ than the "green code" $($with $t = 8)$.
- So the results of both codes are rather disappointing.
$\text{Conclusion:}$
- Reed–Solomon codes are not very good at the memoryless AWGN channel. Both codes are more than $4 \, \rm dB$ away from the information-theoretical $\text{Shannon bound }$ .
- But Reed–Solomon codes are very effective with so-called $\text{Burst Error Channels}$. They are therefore mainly used for fading channels, memory systems, etc.
- Reed–Solomon codes are not perfect. The consequences of this are covered in "Exercise 2.16".
Typical applications with Reed–Solomon coding
Reed–Solomon coding is often applied according to the diagram together with an "inner code" in cascaded form.
- The inner code is almost always a binary code and in satellite– and mobile communications often a convolutional code.
- If one wishes to study only Reed–Solomon encoding/decoding, one replaces the grayed components in a simulation with a single block called a "super channel".
- Concatenated coding systems are very efficient if an interleaver is connected between the two encoders to further relax burst errors.
$\text{Example 3:}$ The diagram shows an example of such an interleaver, where we restrict ourselves to a $20 × 4$ matrix. In practice, these matrices are significantly larger.
The interleaver is written row–by–row and read out column–by–column $($blue label$)$. With the de–interleaver $($green label$)$ the sequence is exactly the other way round.
- The Reed–Solomon symbols are therefore not forwarded to the inner coder consecutively, but according to the specified sequence as symbol 1, 21, 41, 61, 2, 22, etc. .
- A contiguous area $($here the symbols 42, 62, 3, 23, 43, 63, 4, 24 ⇒ around the rectangle outlined in red below$)$ is destroyed on the channel, for example by a scratch on the channel "storage medium".
- After de–interleaving, the symbol sequence is again 1, 2, 3, ...
You can see from the red outlined circles that now this burst error has been largely "broken up".
$\text{Example 4:}$ A very widely used application of Reed–Solomon coding – and also the most commercially successful – is the »Compact Disc« $\rm (CD)$, whose error correction mechanism has already been described in the "introduction chapter" $($Example 7$)$ of this book. Here the inner code is also a Reed–Solomon code, and the concatenated coding system can be described as follows:
- Both channels of the stereo–audio signal are sampled at $\text{44.1 kHz}$ each and every sample is digitally represented at $32$ bits $($four bytes$)$.
- The grouping of six samples results in a frame $(192$ Bit$)$ and thus $24$ code symbols from the Galois field $\rm GF(2^8)$. Each code symbol thus corresponds to exactly one byte.
- The first Reed–Solomon code with rate $R_1 = 24/28$ returns $28$ bytes, which are fed to an interleaver of size $28 × 109$ bytes. The readout is done (complicated) diagonally.
- The interleaver distributes contiguous bytes over a large area of the entire disc. This resolves so-called "bursts" e.g. caused by scratches on the $\rm CD$.
- Together with the second Reed–Solomon code $($rate $R_2 = 28/32)$ gives a total rate of $R = (24/28) · (28/32) = 3/4$. Both codes can each correct $t = 2$ symbol errors.
- The two component codes $\text{RSC (28, 24, 5)}$ and $\text{RSC (32, 28, 5)}$ are each based on the Galois field $\rm GF(2^8)$, which would actually mean a code length of $n = 255$ .
- The shorter component codes needed here result from the $\text{RSC (255, 251, 5)}_{256}$ by "shortening" ⇒ see "Exercise 1.9Z". However, this measure does not change the minimum distance $d_{\rm min}= 5$ .
- With the subsequent $\text{Eight to Fourteen Modulation}$ and further control symbols, one finally arrives at the final code rate $ R = 192/588 ≈ 0.326$ of the CD data compression.
In the section "Slit CD" you can see for yourself the correction capabilities of this "cross–interleaved Reed–Solomon coding" with the help of an audio example, but you will also see its limitations
.
Exercises for the chapter
Exercise 2.15: Block Error Probability with AWGN
Exercise 2.15Z: Block Error Probability once more
Exercise 2.16: Bounded Distance Decoding: Decision Regions
References
- ↑ Liva, G.: Channel Coding. Lecture Notes, Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010.