Difference between revisions of "Aufgaben:Exercise 4.13: Decoding LDPC Codes"
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes}} |
| − | [[File:P_ID3083__KC_A_4_13_v1.png|right|frame| | + | [[File:P_ID3083__KC_A_4_13_v1.png|right|frame|Given LDPC parity-check matrix]] |
| − | + | The exercise deals with [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Iterative_decoding_of_LDPC_codes|"Iterative decoding of LDPC–codes"]] according to the ''Message passing algorithm''. | |
| − | + | The starting point is the presented $9 × 12$ parity-check matrix $\mathbf{H}$, which is to be represented as Tanner graph at the beginning of the exercise. It should be noted: | |
| − | + | # The "variable nodes" $V_i$ denote the $n$ bits of the code word. | |
| − | + | # The "check nodes" $C_j$ represent the $m$ parity-check equations. | |
| − | + | # A connection between $V_i$ and $C_j$ indicates that the element of matrix $\mathbf{H}$ $($in row $j$, column $i)$ is $h_{j,\hspace{0.05cm} i} =1$. | |
| − | + | #For $h_{j,\hspace{0.05cm}i} = 0$ there is no connection between $V_i$ and $C_j$. | |
| + | # The "neighbors $N(V_i)$ of $V_i$" is called the set of all check nodes $C_j$ connected to $V_i$ in the Tanner graph. | ||
| + | #Correspondingly, to $N(C_j)$ belong all variable nodes $V_i$ with a connection to $C_j$. | ||
| − | + | The decoding is performed alternately with respect to | |
| − | * | + | * the variable nodes ⇒ "variable nodes decoder" $\rm (VND)$, and |
| − | |||
| + | * the check nodes ⇒ "check nodes decoder" $\rm (CND)$. | ||
| − | |||
| + | This is referred to in subtasks '''(5)''' and '''(6)'''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <u>Hints:</u> | ||
| + | *The exercise belongs to the chapter [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes| "Basic information about Low–density Parity–check Codes"]]. | ||
| + | *Reference is made in particular to the section [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Iterative_decoding_of_LDPC_codes|"Iterative decoding of LDPC codes"]]. | ||
| + | |||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How many variable nodes $(I_{\rm VN})$ and check nodes $(I_{\rm CN})$ are to be considered? |
|type="{}"} | |type="{}"} | ||
$I_{\rm VN} \ = \ ${ 12 } | $I_{\rm VN} \ = \ ${ 12 } | ||
$I_{\rm CN} \ = \ ${ 9 } | $I_{\rm CN} \ = \ ${ 9 } | ||
| − | { | + | {Which of the following check nodes and variable nodes are connected? |
|type="[]"} | |type="[]"} | ||
| − | + $C_4$ | + | + $C_4$ and $V_6$. |
| − | + $C_5$ | + | + $C_5$ and $V_5$. |
| − | - $C_6$ | + | - $C_6$ and $V_4$. |
| − | - $C_6$ | + | - $C_6$ and $V_i$ for $i > 9$. |
| − | + $C_j$ | + | + $C_j$ and $V_{j-1}$ for $j > 6$. |
| − | { | + | {Which statements are true regarding neighbors $N(V_i)$ and $N(C_j)$ ? |
|type="[]"} | |type="[]"} | ||
- $N(V_1) = \{C_1, \ C_2, \ C_3, \ C_4\}$, | - $N(V_1) = \{C_1, \ C_2, \ C_3, \ C_4\}$, | ||
| Line 50: | Line 54: | ||
- $N(C_9) = \{V_3, \ V_5, \ V_7\}$. | - $N(C_9) = \{V_3, \ V_5, \ V_7\}$. | ||
| − | { | + | {Which statements are true for the variable node decoder $\rm (VND)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + At the beginning $($iteration 0$)$ the $L$–values of the nodes $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \ V_n$ are preassigned corresponding to the channel input values $y_i$. |
| − | + | + | + For the VND represents $L(C_j → V_i)$ a-priori information. |
| − | - | + | - There are analogies between the "variable node decoder" and the decoding of a single parity–check code. |
| − | { | + | {Which statements are true for the check node decoder $\rm (CND)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The CND returns at the end the desired a-posteriori $L$–values. |
| − | - | + | - For the CND represents $L(C_j → V_i)$ a-priori information. |
| − | + | + | + There are analogies between the "check node decoder" and the decoding of a single parity–check code. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The variable node $V_i$ stands for the $i$<sup>th</sup> code word bit, so that $I_{\rm VN}$ is equal to the code word length $n$. |
| − | * | + | *From the column number of the $\mathbf{H}$ matrix, we can see $I_{\rm VN} = n \ \underline{= 12}$. |
| − | * | + | |
| − | * | + | *For the set of all variable nodes, one can thus write in general: ${\rm VN} = \{V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , V_i, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_n\}$. |
| − | * | + | |
| + | *The check node $ C_j$ represents the $j$<sup>th</sup> parity-check equation, and for the set of all check nodes: | ||
| + | :$${\rm CN} = \{C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_j, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_m\}.$$ | ||
| + | *From the number of rows of the $\mathbf{H}$ matrix we get $I_{\rm CN} \ \underline {= m = 9}$. | ||
| + | |||
| + | |||
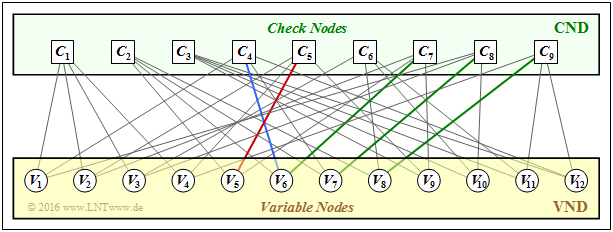
| + | [[File:P_ID3084__KC_A_4_13c_v1.png|right|frame|Tanner graph for the present example ]] | ||
| + | |||
| + | '''(2)''' The results can be read from the Tanner graph sketched on the right. | ||
| + | |||
| + | Correct are <u>the proposed solutions 1, 2 and 5</u>: | ||
| + | * The element $h_{5,\hspace{0.05cm}5}=1$ $($column 5, row 5$)$ ⇒ red edge. | ||
| + | |||
| + | * The element $h_{4,\hspace{0.05cm} 6}=1$ $($column 4, row 6$)$ ⇒ blue edge. | ||
| + | |||
| + | * The element $h_{6, \hspace{0.05cm}4}=0$ $($column 6, row 4$)$ ⇒ no edge. | ||
| + | |||
| + | * $h_{6,\hspace{0.05cm} 10} = h_{6,\hspace{0.05cm} 11} = 1$, $h_{6,\hspace{0.05cm}12} = 0$ ⇒ not all three edges exist. | ||
| + | |||
| + | * It holds $h_{7,\hspace{0.05cm}6} = h_{8,\hspace{0.05cm}7} = h_{9,\hspace{0.05cm}8} = 1$ ⇒ green edges. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' It is a regular LDPC code with | ||
| + | * $w_{\rm R}(j) = 4 = w_{\rm R}$ for $1 ≤ j ≤ 9$, | ||
| + | |||
| + | * $w_{\rm C}(i) = 3 = w_{\rm C}$ for $1 ≤ i ≤ 12$. | ||
| + | |||
| + | |||
| + | The <u>answers 2 and 3</u> are correct, as can be seen from the first row and ninth column, respectively, of the parity-check matrix $\mathbf{H}$. | ||
| + | |||
| + | The Tanner graph confirms these results: | ||
| + | * From $C_1$ there are edges to $V_1, \ V_2, \ V_3$, and $V_4$. | ||
| + | * From $V_9$ there are edges to $C_3, \ C_5$, and $C_7$. | ||
| − | |||
| − | + | The answers 1 and 4 cannot be correct already because | |
| + | * the neighborhood $N(V_i)$ of each variable node $V_i$ contains exactly $w_{\rm C} = 3$ elements, and | ||
| − | + | * the neighborhood $N(C_j)$ of each check node $C_j$ contains exactly $w_{\rm R} = 4$ elements. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Correct are the <u>proposed solutions 1 and 2</u>, as can be seen from the [[Channel_Coding/The_Basics_of_Low-Density_Parity_Check_Codes#Iterative_decoding_of_LDPC_codes|"corresponding theory page"]]: | |
| − | * | + | * At the start of decoding $($so to speak at iteration $I=0)$ the $L$–values of the variable nodes ⇒ $L(V_i)$ are preallocated with the channel input values. |
| − | |||
| − | + | * Later $($from iteration $I = 1)$ the log likelihood ratio $L(C_j → V_i)$ transmitted by the CND is considered in the VND as a-priori information. | |
| − | * | ||
| − | |||
| + | * Answer 3 is wrong. Rather, the correct answer would be: There are analogies between the VND algorithm and the decoding of a "repetition code". | ||
| − | '''( | + | '''(5)''' Correct is <u>only proposed solution 3</u> because |
| − | + | * the final a-posteriori $L$–values are derived from the VND, not from the CND; | |
| − | * | ||
| − | |||
| + | * the $L$–value $L(C_j → V_i)$ represents extrinsic information for the CND; and | ||
| − | + | * there are indeed analogies between the CND algorithm and SPC decoding. | |
| − | * | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^4.4 Low–density Parity–check Codes^]] |
Latest revision as of 18:30, 17 December 2022
The exercise deals with "Iterative decoding of LDPC–codes" according to the Message passing algorithm.
The starting point is the presented $9 × 12$ parity-check matrix $\mathbf{H}$, which is to be represented as Tanner graph at the beginning of the exercise. It should be noted:
- The "variable nodes" $V_i$ denote the $n$ bits of the code word.
- The "check nodes" $C_j$ represent the $m$ parity-check equations.
- A connection between $V_i$ and $C_j$ indicates that the element of matrix $\mathbf{H}$ $($in row $j$, column $i)$ is $h_{j,\hspace{0.05cm} i} =1$.
- For $h_{j,\hspace{0.05cm}i} = 0$ there is no connection between $V_i$ and $C_j$.
- The "neighbors $N(V_i)$ of $V_i$" is called the set of all check nodes $C_j$ connected to $V_i$ in the Tanner graph.
- Correspondingly, to $N(C_j)$ belong all variable nodes $V_i$ with a connection to $C_j$.
The decoding is performed alternately with respect to
- the variable nodes ⇒ "variable nodes decoder" $\rm (VND)$, and
- the check nodes ⇒ "check nodes decoder" $\rm (CND)$.
This is referred to in subtasks (5) and (6).
Hints:
- The exercise belongs to the chapter "Basic information about Low–density Parity–check Codes".
- Reference is made in particular to the section "Iterative decoding of LDPC codes".
Questions
Solution
- From the column number of the $\mathbf{H}$ matrix, we can see $I_{\rm VN} = n \ \underline{= 12}$.
- For the set of all variable nodes, one can thus write in general: ${\rm VN} = \{V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , V_i, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_n\}$.
- The check node $ C_j$ represents the $j$th parity-check equation, and for the set of all check nodes:
- $${\rm CN} = \{C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_j, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_m\}.$$
- From the number of rows of the $\mathbf{H}$ matrix we get $I_{\rm CN} \ \underline {= m = 9}$.
(2) The results can be read from the Tanner graph sketched on the right.
Correct are the proposed solutions 1, 2 and 5:
- The element $h_{5,\hspace{0.05cm}5}=1$ $($column 5, row 5$)$ ⇒ red edge.
- The element $h_{4,\hspace{0.05cm} 6}=1$ $($column 4, row 6$)$ ⇒ blue edge.
- The element $h_{6, \hspace{0.05cm}4}=0$ $($column 6, row 4$)$ ⇒ no edge.
- $h_{6,\hspace{0.05cm} 10} = h_{6,\hspace{0.05cm} 11} = 1$, $h_{6,\hspace{0.05cm}12} = 0$ ⇒ not all three edges exist.
- It holds $h_{7,\hspace{0.05cm}6} = h_{8,\hspace{0.05cm}7} = h_{9,\hspace{0.05cm}8} = 1$ ⇒ green edges.
(3) It is a regular LDPC code with
- $w_{\rm R}(j) = 4 = w_{\rm R}$ for $1 ≤ j ≤ 9$,
- $w_{\rm C}(i) = 3 = w_{\rm C}$ for $1 ≤ i ≤ 12$.
The answers 2 and 3 are correct, as can be seen from the first row and ninth column, respectively, of the parity-check matrix $\mathbf{H}$.
The Tanner graph confirms these results:
- From $C_1$ there are edges to $V_1, \ V_2, \ V_3$, and $V_4$.
- From $V_9$ there are edges to $C_3, \ C_5$, and $C_7$.
The answers 1 and 4 cannot be correct already because
- the neighborhood $N(V_i)$ of each variable node $V_i$ contains exactly $w_{\rm C} = 3$ elements, and
- the neighborhood $N(C_j)$ of each check node $C_j$ contains exactly $w_{\rm R} = 4$ elements.
(4) Correct are the proposed solutions 1 and 2, as can be seen from the "corresponding theory page":
- At the start of decoding $($so to speak at iteration $I=0)$ the $L$–values of the variable nodes ⇒ $L(V_i)$ are preallocated with the channel input values.
- Later $($from iteration $I = 1)$ the log likelihood ratio $L(C_j → V_i)$ transmitted by the CND is considered in the VND as a-priori information.
- Answer 3 is wrong. Rather, the correct answer would be: There are analogies between the VND algorithm and the decoding of a "repetition code".
(5) Correct is only proposed solution 3 because
- the final a-posteriori $L$–values are derived from the VND, not from the CND;
- the $L$–value $L(C_j → V_i)$ represents extrinsic information for the CND; and
- there are indeed analogies between the CND algorithm and SPC decoding.