Difference between revisions of "Theory of Stochastic Signals/Power-Spectral Density"
| (36 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Random Variables with Statistical Dependence |
| − | |Vorherige Seite= | + | |Vorherige Seite=Auto-Correlation Function |
| − | |Nächste Seite= | + | |Nächste Seite=Cross-Correlation Function and Cross Power Density |
}} | }} | ||
| − | == | + | ==Wiener-Khintchine Theorem== |
<br> | <br> | ||
| − | + | In the remainder of this paper we restrict ourselves to ergodic processes. As was shown in the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Ergodic_random_processes|"last chapter"]] the following statements then hold: | |
| − | * | + | *Each individual pattern function $x_i(t)$ is representative of the entire random process $\{x_i(t)\}$. |
| − | * | + | *All time means are thus identical to the corresponding coulter means. |
| − | * | + | *The auto-correlation function, which is generally affected by the two time parameters $t_1$ and $t_2$, now depends only on the time difference $τ = t_2 - t_1$: |
:$$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$ | :$$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$ | ||
| − | + | The auto-correlation function provides quantitative information about the (linear) statistical bindings within the ergodic process $\{x_i(t)\}$ in the time domain. The equivalent descriptor in the frequency domain is the "power-spectral density", often also referred to as the "power-spectral density". | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ The »'''power-spectral density'''« $\rm (PSD)$ of an ergodic random process $\{x_i(t)\}$ is the Fourier transform of the auto-correlation function $\rm (ACF)$: |
:$${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$ | :$${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$ | ||
| − | + | This functional relationship is called the "Theorem of [https://en.wikipedia.org/wiki/Norbert_Wiener $\text{Wiener}$] and [https://en.wikipedia.org/wiki/Aleksandr_Khinchin $\text{Khinchin}$]". }} | |
| − | + | Similarly, the auto-correlation function can be computed as the inverse Fourier transform of the power-spectral density (see section [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|"Inverse Fourier transform"]] in the book "Signal Representation"): | |
| − | :$$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x | + | :$$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} f.$$ |
| − | * | + | *The two equations are directly applicable only if the random process contains neither a DC component nor periodic components. |
| − | * | + | *Otherwise, one must proceed according to the specifications given in section [[Theory_of_Stochastic_Signals/Power-Spectral_Density#Power-spectral_density_with_DC_component|"Power-spectral density with DC component"]]. |
| − | == | + | ==Physical interpretation and measurement== |
<br> | <br> | ||
| − | + | The lower chart shows an arrangement for (approximate) metrological determination of the power-spectral density ${\it \Phi}_x(f)$. The following should be noted in this regard: | |
| − | + | *The random signal $x(t)$ is applied to a (preferably) rectangular and (preferably) narrowband filter with center frequency $f$ and bandwidth $Δf$ where $Δf$ must be chosen sufficiently small according to the desired frequency resolution. | |
| − | + | *The corresponding output signal $x_f(t)$ is squared and then the mean value is formed over a sufficiently long measurement period $T_{\rm M}$. This gives the "power of $x_f(t)$" or the "power components of $x(t)$ in the spectral range from $f - Δf/2$ to $f + Δf/2$": | |
| − | + | [[File: P_ID387__Sto_T_4_5_S2_neu.png |right|frame| To measure the power-spectral density]] | |
| − | |||
| − | * | ||
| − | * | ||
:$$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$ | :$$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$ | ||
| − | * | + | *Division by $Δf$ leads to the power-spectral density $\rm (PSD)$: |
| − | :$${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} | + | :$${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} \Rightarrow \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$ |
| − | + | *${\it \Phi}_{x+}(f) = 2 \cdot {\it \Phi}_x(f)$ denotes the one-sided PSD defined only for positive frequencies. For $f<0$ ⇒ ${\it \Phi}_{x+}(f) = 0$. In contrast, for the commonly used two-sided power-spectral density: | |
| − | * | + | :$${\it \Phi}_x(-f) = {\it \Phi}_x(f).$$ |
| + | *While the power $P_{x_f}$ tends to zero as the bandwidth $Δf$ becomes smaller, the power-spectral density remains nearly constant above a sufficiently small value of $Δf$. For the exact determination of ${\it \Phi}_x(f)$ two boundary crossings are necessary: | ||
:$${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$ | :$${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | * | + | *From this physical interpretation it further follows that the power-spectral density is always real and can never become negative. |
| − | * | + | *The total power of the random signal $x(t)$ is then obtained by integration over all spectral components: |
:$$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$}} | :$$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$}} | ||
| − | == | + | ==Reciprocity law of ACF duration and PSD bandwidth== |
<br> | <br> | ||
| − | + | All the [[Signal_Representation/Fourier_Transform_Laws|$\text{Fourier transform theorems}$]] derived in the book "Signal Representation" for deterministic signals can also be applied to | |
| + | [[File:P_ID390__Sto_T_4_5_S3_Ganz_neu.png |frame| On the "Reciprocity Theorem" of ACF and PSD]] | ||
| − | + | *the auto-correlation function $\rm (ACF)$, and | |
| − | + | *the power-spectral density $\rm (PSD)$. | |
| − | * | + | <br>However, not all laws yield meaningful results due to the specific properties |
| − | * | + | *of auto-correlation function (always real and even) |
| + | *and power-spectral density (always real, even, and non–negative). | ||
| + | |||
| + | We now consider as in the section [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Interpretation_of_the_auto-correlation_function|"Interpretation of the auto-correlation function"]] two different ergodic random processes $\{x_i(t)\}$ and $\{y_i(t)\}$ based on | ||
| + | #two pattern signals $x(t)$ and $y(t)$ ⇒ upper sketch, | ||
| + | #two auto-correlation functions $φ_x(τ)$ and $φ_y(τ)$ ⇒ middle sketch, | ||
| + | #two power-spectral densities ${\it \Phi}_x(f)$ and ${\it \Phi}_y(f)$ ⇒ bottom sketch. | ||
| − | |||
| − | + | Based on these exemplary graphs, the following statements can be made: | |
| − | + | *The areas under the PSD curves are equal ⇒ the processes $\{x_i(t)\}$ and $\{y_i(t)\}$ have the same power: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
:$${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$ | :$${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$ | ||
| − | * | + | *The from classical (deterministic) system theory well known [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|$\text{Reciprocity Theorem of time duration and bandwidth}$]] also applies here: '''A narrow ACF corresponds to a broad PSD and vice versa'''. |
| − | * | + | *As a descriptive quantity, we use here the »'''equivalent PSD bandwidth'''« $∇f$ $($one speaks "Nabla-f"$)$, <br>similarly defined as the equivalent ACF duration $∇τ$ in chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Interpretation_of_the_auto-correlation_function|"Interpretation of the auto-correlation function"]]: |
| − | :$${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, | + | :$${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, $$ |
| − | * | + | :$${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$ |
| − | :$${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm | + | *With these definitions, the following basic relationship holds: |
| + | :$${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm resp.}\hspace{1cm} | ||
{{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$ | {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ We start from the graph at the top of this section: |
| − | * | + | *The characteristics of the higher frequency signal $x(t)$ are $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ and $∇f_x = 3 \hspace{0.08cm} \rm MHz$. |
| − | * | + | *The equivalent ACF duration of the signal $y(t)$ is three times: $∇τ_y = 1 \hspace{0.08cm} \rm µs$. |
| − | * | + | *The equivalent PSD bandwidth of the signal $y(t)$ is thus only $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$. }} |
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{General:}$ |
| − | + | '''The product of equivalent ACF duration ${ {\rm \nabla} \tau_x}$ and equivalent PSD bandwidth $ { {\rm \nabla} f_x}$ is always "one"''': | |
| − | :$${ {\rm \nabla} \tau_x} \cdot | + | :$${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$}} |
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{Proof:}$ According to the above definitions: |
| − | :$${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it | + | :$${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it \Phi}_x(f = {\rm 0)} }{ \varphi_x(\tau = \rm 0)},$$ |
| − | :$${ {\rm \nabla} f_x} = \frac {1}{ {\it | + | :$${ {\rm \nabla} f_x} = \frac {1}{ {\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{ {\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)} }{ {\it \Phi}_x(f = \rm 0)}.$$ |
| − | + | Thus, the product is equal to $1$. | |
<div align="right">'''q.e.d.'''</div> }} | <div align="right">'''q.e.d.'''</div> }} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ |
| − | + | A limiting case of the reciprocity theorem represents the so-called "White Noise": | |
| − | * | + | *This includes all spectral components (up to infinity). |
| − | * | + | *The equivalent PSD bandwidth $∇f$ is infinite. |
| − | + | The theorem given here states that for the equivalent ACF duration $∇τ = 0$ must hold ⇒ »'''white noise has a Dirac-shaped ACF'''«. | |
| − | + | For more on this topic, see the three-part (German language) learning video [[Der_AWGN-Kanal_(Lernvideo)|"The AWGN channel"]], especially the second part.}} | |
| − | == | + | ==Power-spectral density with DC component== |
<br> | <br> | ||
| − | + | We assume a DC–free random process $\{x_i(t)\}$. Further, we assume that the process also contains no periodic components. Then holds: | |
| − | * | + | *The auto-correlation function $φ_x(τ)$ vanishes for $τ → ∞$. |
| − | * | + | *The power-spectral density ${\it \Phi}_x(f)$ – computable as the Fourier transform of $φ_x(τ)$ – is both continuous in value and continuous in time, i.e., without discrete components. |
| − | + | We now consider a second random process $\{y_i(t)\}$, which differs from the process $\{x_i(t)\}$ only by an additional DC component $m_y$: | |
| − | :$$\left\{ y_i (t) | + | :$$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$ |
| − | + | The statistical descriptors of the mean-valued random process $\{y_i(t)\}$ then have the following properties: | |
| − | * | + | *The limit of the ACF for $τ → ∞$ is now no longer zero, but $m_y^2$. Throughout the $τ$–range from $-∞$ to $+∞$ the ACF $φ_y(τ)$ is larger than $φ_x(τ)$ by $m_y^2$: |
:$${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$ | :$${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$ | ||
| − | * | + | *According to the elementary laws of the Fourier transform, the constant ACF contribution in the PSD leads to a Dirac delta function $δ(f)$ with weight $m_y^2$: |
| − | :$${{\it | + | :$${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$ |
| − | + | *More information about the $\delta$–function can be found in the chapter [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal|"Direct current signal - Limit case of a periodic signal"]] of the book "Signal Representation". Furthermore, we would like to refer you here to the (German language) learning video [[Herleitung_und_Visualisierung_der_Diracfunktion_(Lernvideo)|"Herleitung und Visualisierung der Diracfunktion"]] ⇒ "Derivation and visualization of the Dirac delta function". | |
| − | |||
| − | == | + | ==Numerical PSD determination== |
<br> | <br> | ||
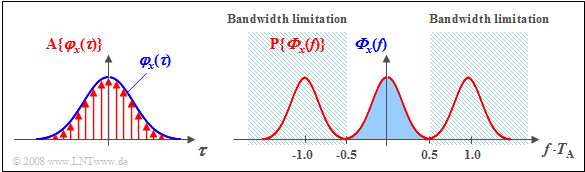
| − | + | Auto-correlation function and power-spectral density are strictly related via the [[Signal_Representation/Fourier_Transform_and_its_Inverse#Fourier_transform|$\text{Fourier transform}$]]. This relationship also holds for discrete-time ACF representation with the sampling operator ${\rm A} \{ \varphi_x ( \tau ) \} $, thus for | |
:$${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$ | :$${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$ | ||
| − | + | The transition from the time domain to the spectral domain can be derived with the following steps: | |
| − | * | + | *The distance $T_{\rm A}$ of two samples is determined by the absolute bandwidth $B_x$ $($maximum occurring frequency within the process$)$ via the sampling theorem: |
:$$T_{\rm A}\le\frac{1}{2B_x}.$$ | :$$T_{\rm A}\le\frac{1}{2B_x}.$$ | ||
| − | * | + | *The Fourier transform of the discrete-time (sampled) auto-correlation function yields an with ${\rm 1}/T_{\rm A}$ periodic power-spectral density: |
:$${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$ | :$${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$ | ||
| − | {{BlaueBox|TEXT= | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{Conclusion:}$ Since both $φ_x(τ)$ and ${\it \Phi}_x(f)$ are even and real functions, the following relation holds: |
| − | :$${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot | + | :$${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$ |
| − | * | + | *The power-spectral density $\rm (PSD)$ of the continuous-time process is obtained from ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ by bandlimiting to the range $\vert f \vert ≤ 1/(2T_{\rm A})$. |
| − | * | + | *In the time domain, this operation means interpolating the individual ACF samples with the ${\rm sinc}$ function, where ${\rm sinc}(x)$ stands for $\sin(\pi x)/(\pi x)$.}} |
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 3:}$ A Gaussian ACF $φ_x(τ)$ is sampled at distance $T_{\rm A}$ where the sampling theorem is satisfied: | ||
| + | [[File:EN_Sto_T_4_5_S5.png |right|frame| Discrete-time auto-correlation function, periodically continued power-spectral density]] | ||
| + | *The Fourier transform of the discrete-time ACF ⇒ ${\rm A} \{φ_x(τ) \}$ be the periodically continued PSD ⇒ ${\rm P} \{ { {\it \Phi}_x} ( f) \}$. | ||
| + | |||
| + | *This with ${\rm 1}/T_{\rm A}$ periodic function ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ is accordingly infinitely extended (red curve). | ||
| − | + | ||
| − | + | *The PSD ${\it \Phi}_x(f)$ of the continuous-time process $\{x_i(t)\}$ is obtained by band-limiting to the frequency range $\vert f \cdot T_{\rm A} \vert ≤ 0.5$, highlighted in blue in the figure. }} | |
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | == | + | ==Accuracy of the numerical PSD calculation== |
<br> | <br> | ||
| − | + | For the following analysis, we make the following assumptions: | |
| − | + | #The discrete-time ACF $φ_x(k \cdot T_{\rm A})$ was determined numerically from $N$ samples. | |
| − | + | #As already shown in section [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Accuracy_of_the_numerical_ACF_calculation|"Accuracy of the numerical ACF calculation"]], these values are in error and the errors are correlated if $N$ was chosen too small. | |
| − | :$${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} k T_{\rm A}).$$ | + | #To calculate the periodic power-spectral density $\rm (PSD)$, we use only the ACF values $φ_x(0)$, ... , $φ_x(K \cdot T_{\rm A})$: |
| + | ::$${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$ | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | + | The accuracy of the power-spectral density calculation is determined to a strong extent by the parameter $K$: | |
| − | * | + | *If $K$ is chosen too small, the ACF values actually present $φ_x(k - T_{\rm A})$ with $k > K$ will not be taken into account. |
| − | * | + | *If $K$ is too large, also such ACF values are considered, which should actually be zero and are finite only because of the numerical ACF calculation. |
| − | * | + | *These values are only errors $($due to a small $N$ in the ACF calculation$)$ and impair the PSD calculation more than they provide a useful contribution to the result. }} |
| + | |||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Example 4:}$ We consider here a zero mean process with statistically independent samples. Thus, only the ACF value $φ_x(0) = σ_x^2$ should be different from zero. | ||
| + | [[File:EN_Sto_T_4_5_S5_b_neu_v2.png |450px|right|frame| Accuracy of numerical PSD calculation ]] | ||
| + | *But if one determines the ACF numerically from only $N = 1000$ samples, one obtains finite ACF values even for $k ≠ 0$. | ||
| + | *The upper figure shows that these erroneous ACF values can be up to $6\%$ of the maximum value. | ||
| + | |||
| + | *The numerically determined PSD is shown below. The theoretical (yellow) curve should be constant for $\vert f \cdot T_{\rm A} \vert ≤ 0.5$. | ||
| + | |||
| + | *The green and purple curves illustrate how by $K = 3$ resp. $K = 10$, the result is distorted compared to $K = 0$. | ||
| + | |||
| + | *In this case $($statistically independent random variables$)$ the error grows monotonically with increasing $K$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In contrast, for a random variable with statistical bindings, there is an optimal value for $K$ in each case. | |
| − | + | #If this is chosen too small, significant bindings are not considered. | |
| − | + | #In contrast, a too large value leads to oscillations that can only be attributed to erroneous ACF values.}} | |
| − | |||
| − | In | ||
| − | |||
| − | |||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.12:_Power-Spectral_Density_of_a_Binary_Signal|Exercise 4.12: Power-Spectral Density of a Binary Signal]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.12Z:_White_Gaussian_Noise|Exercise 4.12Z: White Gaussian Noise]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.13:_Gaussian_ACF_and_PSD|Exercise 4.13: Gaussian ACF and PSD]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_4.13Z:_AMI_Code|Exercise 4.13Z: AMI Code]] |
{{Display}} | {{Display}} | ||
Latest revision as of 16:13, 22 December 2022
Contents
Wiener-Khintchine Theorem
In the remainder of this paper we restrict ourselves to ergodic processes. As was shown in the "last chapter" the following statements then hold:
- Each individual pattern function $x_i(t)$ is representative of the entire random process $\{x_i(t)\}$.
- All time means are thus identical to the corresponding coulter means.
- The auto-correlation function, which is generally affected by the two time parameters $t_1$ and $t_2$, now depends only on the time difference $τ = t_2 - t_1$:
- $$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$
The auto-correlation function provides quantitative information about the (linear) statistical bindings within the ergodic process $\{x_i(t)\}$ in the time domain. The equivalent descriptor in the frequency domain is the "power-spectral density", often also referred to as the "power-spectral density".
$\text{Definition:}$ The »power-spectral density« $\rm (PSD)$ of an ergodic random process $\{x_i(t)\}$ is the Fourier transform of the auto-correlation function $\rm (ACF)$:
- $${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$
This functional relationship is called the "Theorem of $\text{Wiener}$ and $\text{Khinchin}$".
Similarly, the auto-correlation function can be computed as the inverse Fourier transform of the power-spectral density (see section "Inverse Fourier transform" in the book "Signal Representation"):
- $$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} f.$$
- The two equations are directly applicable only if the random process contains neither a DC component nor periodic components.
- Otherwise, one must proceed according to the specifications given in section "Power-spectral density with DC component".
Physical interpretation and measurement
The lower chart shows an arrangement for (approximate) metrological determination of the power-spectral density ${\it \Phi}_x(f)$. The following should be noted in this regard:
- The random signal $x(t)$ is applied to a (preferably) rectangular and (preferably) narrowband filter with center frequency $f$ and bandwidth $Δf$ where $Δf$ must be chosen sufficiently small according to the desired frequency resolution.
- The corresponding output signal $x_f(t)$ is squared and then the mean value is formed over a sufficiently long measurement period $T_{\rm M}$. This gives the "power of $x_f(t)$" or the "power components of $x(t)$ in the spectral range from $f - Δf/2$ to $f + Δf/2$":
- $$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$
- Division by $Δf$ leads to the power-spectral density $\rm (PSD)$:
- $${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} \Rightarrow \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$
- ${\it \Phi}_{x+}(f) = 2 \cdot {\it \Phi}_x(f)$ denotes the one-sided PSD defined only for positive frequencies. For $f<0$ ⇒ ${\it \Phi}_{x+}(f) = 0$. In contrast, for the commonly used two-sided power-spectral density:
- $${\it \Phi}_x(-f) = {\it \Phi}_x(f).$$
- While the power $P_{x_f}$ tends to zero as the bandwidth $Δf$ becomes smaller, the power-spectral density remains nearly constant above a sufficiently small value of $Δf$. For the exact determination of ${\it \Phi}_x(f)$ two boundary crossings are necessary:
- $${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$
$\text{Conclusion:}$
- From this physical interpretation it further follows that the power-spectral density is always real and can never become negative.
- The total power of the random signal $x(t)$ is then obtained by integration over all spectral components:
- $$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$
Reciprocity law of ACF duration and PSD bandwidth
All the $\text{Fourier transform theorems}$ derived in the book "Signal Representation" for deterministic signals can also be applied to
- the auto-correlation function $\rm (ACF)$, and
- the power-spectral density $\rm (PSD)$.
However, not all laws yield meaningful results due to the specific properties
- of auto-correlation function (always real and even)
- and power-spectral density (always real, even, and non–negative).
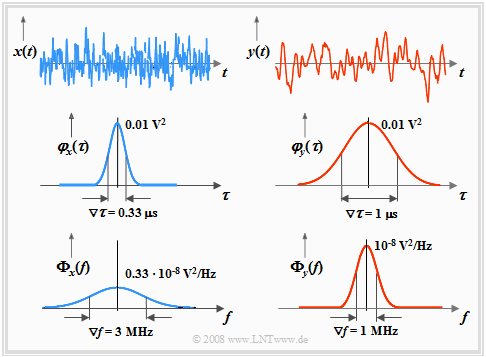
We now consider as in the section "Interpretation of the auto-correlation function" two different ergodic random processes $\{x_i(t)\}$ and $\{y_i(t)\}$ based on
- two pattern signals $x(t)$ and $y(t)$ ⇒ upper sketch,
- two auto-correlation functions $φ_x(τ)$ and $φ_y(τ)$ ⇒ middle sketch,
- two power-spectral densities ${\it \Phi}_x(f)$ and ${\it \Phi}_y(f)$ ⇒ bottom sketch.
Based on these exemplary graphs, the following statements can be made:
- The areas under the PSD curves are equal ⇒ the processes $\{x_i(t)\}$ and $\{y_i(t)\}$ have the same power:
- $${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$
- The from classical (deterministic) system theory well known $\text{Reciprocity Theorem of time duration and bandwidth}$ also applies here: A narrow ACF corresponds to a broad PSD and vice versa.
- As a descriptive quantity, we use here the »equivalent PSD bandwidth« $∇f$ $($one speaks "Nabla-f"$)$,
similarly defined as the equivalent ACF duration $∇τ$ in chapter "Interpretation of the auto-correlation function":
- $${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, $$
- $${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$
- With these definitions, the following basic relationship holds:
- $${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm resp.}\hspace{1cm} {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$
$\text{Example 1:}$ We start from the graph at the top of this section:
- The characteristics of the higher frequency signal $x(t)$ are $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ and $∇f_x = 3 \hspace{0.08cm} \rm MHz$.
- The equivalent ACF duration of the signal $y(t)$ is three times: $∇τ_y = 1 \hspace{0.08cm} \rm µs$.
- The equivalent PSD bandwidth of the signal $y(t)$ is thus only $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$.
$\text{General:}$ The product of equivalent ACF duration ${ {\rm \nabla} \tau_x}$ and equivalent PSD bandwidth $ { {\rm \nabla} f_x}$ is always "one":
- $${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$
$\text{Proof:}$ According to the above definitions:
- $${ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{ \varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau = \frac { {\it \Phi}_x(f = {\rm 0)} }{ \varphi_x(\tau = \rm 0)},$$
- $${ {\rm \nabla} f_x} = \frac {1}{ {\it \Phi}_x(f = {\rm0})} \cdot \int^{+\infty}_{-\infty}{ {\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f = \frac {\varphi_x(\tau = {\rm 0)} }{ {\it \Phi}_x(f = \rm 0)}.$$
Thus, the product is equal to $1$.
$\text{Example 2:}$ A limiting case of the reciprocity theorem represents the so-called "White Noise":
- This includes all spectral components (up to infinity).
- The equivalent PSD bandwidth $∇f$ is infinite.
The theorem given here states that for the equivalent ACF duration $∇τ = 0$ must hold ⇒ »white noise has a Dirac-shaped ACF«.
For more on this topic, see the three-part (German language) learning video "The AWGN channel", especially the second part.
Power-spectral density with DC component
We assume a DC–free random process $\{x_i(t)\}$. Further, we assume that the process also contains no periodic components. Then holds:
- The auto-correlation function $φ_x(τ)$ vanishes for $τ → ∞$.
- The power-spectral density ${\it \Phi}_x(f)$ – computable as the Fourier transform of $φ_x(τ)$ – is both continuous in value and continuous in time, i.e., without discrete components.
We now consider a second random process $\{y_i(t)\}$, which differs from the process $\{x_i(t)\}$ only by an additional DC component $m_y$:
- $$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$
The statistical descriptors of the mean-valued random process $\{y_i(t)\}$ then have the following properties:
- The limit of the ACF for $τ → ∞$ is now no longer zero, but $m_y^2$. Throughout the $τ$–range from $-∞$ to $+∞$ the ACF $φ_y(τ)$ is larger than $φ_x(τ)$ by $m_y^2$:
- $${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$
- According to the elementary laws of the Fourier transform, the constant ACF contribution in the PSD leads to a Dirac delta function $δ(f)$ with weight $m_y^2$:
- $${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$
- More information about the $\delta$–function can be found in the chapter "Direct current signal - Limit case of a periodic signal" of the book "Signal Representation". Furthermore, we would like to refer you here to the (German language) learning video "Herleitung und Visualisierung der Diracfunktion" ⇒ "Derivation and visualization of the Dirac delta function".
Numerical PSD determination
Auto-correlation function and power-spectral density are strictly related via the $\text{Fourier transform}$. This relationship also holds for discrete-time ACF representation with the sampling operator ${\rm A} \{ \varphi_x ( \tau ) \} $, thus for
- $${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$
The transition from the time domain to the spectral domain can be derived with the following steps:
- The distance $T_{\rm A}$ of two samples is determined by the absolute bandwidth $B_x$ $($maximum occurring frequency within the process$)$ via the sampling theorem:
- $$T_{\rm A}\le\frac{1}{2B_x}.$$
- The Fourier transform of the discrete-time (sampled) auto-correlation function yields an with ${\rm 1}/T_{\rm A}$ periodic power-spectral density:
- $${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$
$\text{Conclusion:}$ Since both $φ_x(τ)$ and ${\it \Phi}_x(f)$ are even and real functions, the following relation holds:
- $${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
- The power-spectral density $\rm (PSD)$ of the continuous-time process is obtained from ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ by bandlimiting to the range $\vert f \vert ≤ 1/(2T_{\rm A})$.
- In the time domain, this operation means interpolating the individual ACF samples with the ${\rm sinc}$ function, where ${\rm sinc}(x)$ stands for $\sin(\pi x)/(\pi x)$.
$\text{Example 3:}$ A Gaussian ACF $φ_x(τ)$ is sampled at distance $T_{\rm A}$ where the sampling theorem is satisfied:
- The Fourier transform of the discrete-time ACF ⇒ ${\rm A} \{φ_x(τ) \}$ be the periodically continued PSD ⇒ ${\rm P} \{ { {\it \Phi}_x} ( f) \}$.
- This with ${\rm 1}/T_{\rm A}$ periodic function ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ is accordingly infinitely extended (red curve).
- The PSD ${\it \Phi}_x(f)$ of the continuous-time process $\{x_i(t)\}$ is obtained by band-limiting to the frequency range $\vert f \cdot T_{\rm A} \vert ≤ 0.5$, highlighted in blue in the figure.
Accuracy of the numerical PSD calculation
For the following analysis, we make the following assumptions:
- The discrete-time ACF $φ_x(k \cdot T_{\rm A})$ was determined numerically from $N$ samples.
- As already shown in section "Accuracy of the numerical ACF calculation", these values are in error and the errors are correlated if $N$ was chosen too small.
- To calculate the periodic power-spectral density $\rm (PSD)$, we use only the ACF values $φ_x(0)$, ... , $φ_x(K \cdot T_{\rm A})$:
- $${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
$\text{Conclusion:}$ The accuracy of the power-spectral density calculation is determined to a strong extent by the parameter $K$:
- If $K$ is chosen too small, the ACF values actually present $φ_x(k - T_{\rm A})$ with $k > K$ will not be taken into account.
- If $K$ is too large, also such ACF values are considered, which should actually be zero and are finite only because of the numerical ACF calculation.
- These values are only errors $($due to a small $N$ in the ACF calculation$)$ and impair the PSD calculation more than they provide a useful contribution to the result.
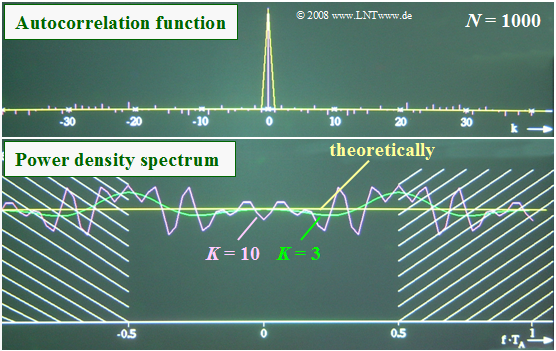
$\text{Example 4:}$ We consider here a zero mean process with statistically independent samples. Thus, only the ACF value $φ_x(0) = σ_x^2$ should be different from zero.
- But if one determines the ACF numerically from only $N = 1000$ samples, one obtains finite ACF values even for $k ≠ 0$.
- The upper figure shows that these erroneous ACF values can be up to $6\%$ of the maximum value.
- The numerically determined PSD is shown below. The theoretical (yellow) curve should be constant for $\vert f \cdot T_{\rm A} \vert ≤ 0.5$.
- The green and purple curves illustrate how by $K = 3$ resp. $K = 10$, the result is distorted compared to $K = 0$.
- In this case $($statistically independent random variables$)$ the error grows monotonically with increasing $K$.
In contrast, for a random variable with statistical bindings, there is an optimal value for $K$ in each case.
- If this is chosen too small, significant bindings are not considered.
- In contrast, a too large value leads to oscillations that can only be attributed to erroneous ACF values.
Exercises for the chapter
Exercise 4.12: Power-Spectral Density of a Binary Signal
Exercise 4.12Z: White Gaussian Noise
Exercise 4.13: Gaussian ACF and PSD