Difference between revisions of "Aufgaben:Exercise 4.1Z: Calculation of Moments"
m (Guenter verschob die Seite 4.01Z Momentenberechnung nach 4.1Z Momentenberechnung) |
|||
| (34 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Differential_Entropy |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_Z_4_1_vers2.png|right|frame|Exponential PDF (top), <br>Laplace PDF (bottom)]] |
| − | + | The upper graph shows the probability density function $\rm (PDF)$ of the [[Theory_of_Stochastic_Signals/Exponentialverteilte_Zufallsgrößen|exponential distribution]]: | |
| − | $$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm | + | :$$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm}x} \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$ |
| − | + | Drawn below is the PDF of the [[Theory_of_Stochastic_Signals/Exponentialverteilte_Zufallsgrößen#Zweiseitige_Exponentialverteilung_.E2.80.93_Laplaceverteilung|Laplace distribution]], which can be specified for all $y$–values as follows: | |
| − | $$f_Y(y) = A_{ Y} \cdot {\rm | + | :$$f_Y(y) = A_{ Y} \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} |\hspace{0.03cm}y\hspace{0.03cm}|}\hspace{0.05cm}.$$ |
| − | + | ||
| − | + | The two continuous random variables $X$ and $Y$ are to be compared with respect to the following characteristics: | |
| − | + | *The linear mean $m_1$ (first order moment), | |
| − | + | *the second order moment ⇒ $m_2$, | |
| − | + | *the variance $\sigma^2 = m_2 - m_1^2$ ⇒ Steiner's theorem, | |
| − | + | *the standard deviation $\sigma$. | |
| − | $$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$ | + | |
| − | $$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The task belongs to the chapter [[Information_Theory/Differentielle_Entropie|Differential Entropy]]. | ||
| + | *Useful hints for solving this task and further information on continuous random variables can be found in the third chapter "Continuous Random Variables" of the book [[Theory of Stochastic Signals]]. | ||
| + | |||
| + | *Also given are the two indefinite integrals: | ||
| + | :$$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$ | ||
| + | :$$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot | ||
(\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) | (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the maximum value $A_X$ of the PDF $f_X(x)$? |
| − | |type=" | + | |type="()"} |
| − | - | + | - $A_X = \lambda/2$, |
| − | + | + | + $A_X = \lambda$, |
| − | - | + | - $A_X = 1/\lambda$. |
| − | { | + | {What is the maximum value $A_Y$ of the PDF $f_Y(y)$? |
| − | |type=" | + | |type="()"} |
| − | + | + | + $A_Y = \lambda/2$, |
| − | - | + | - $A_Y = \lambda$, |
| − | - | + | - $A_Y = 1/\lambda$. |
| − | { | + | {Is there an argument $z$, such that $f_X(z) = f_Y(z)$ ? |
| − | |type=" | + | |type="()"} |
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {Which statements are true about the characteristics of the exponential distribution? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The linear mean is $m_1 = 1/\lambda$. |
| − | + | + | + The second order moment is $m_2 = 2/\lambda^2$. |
| − | + | + | + The variance is $\sigma^2 = 1/\lambda^2$. |
| − | { | + | {Which statements are true about the characteristics of the Laplace distribution? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The linear mean is $m_1 = 1/\lambda$. |
| − | + | + | + The second order moment is $m_2 = 2/\lambda^2$. |
| − | - | + | - The variance is $\sigma^2 = 1/\lambda^2$. |
| − | { | + | {With what probabilities does the random variable $(X$ or $Y)$ differ from the respective mean in magnitude by more than the dispersion $\sigma$? |
|type="{}"} | |type="{}"} | ||
| − | $Exponential: | + | $\text{Exponential:}\; \;{\rm Pr}( |X - m_X| > \sigma_X) \ = \ $ { 0.135 3% } |
| − | $Laplace: | + | $\text{Laplace:}\; \;{\rm Pr}( |Y - m_Y| > \sigma_Y) \ = \ $ { 0.243 3% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | < | + | '''(1)''' <u>Proposed solution 2</u> is correct: |
| − | $$A_{X} \cdot\int_{0}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = A_{X} \cdot (-1/\lambda)\cdot\ | + | *The area under the PDF must always be $1$ . It follows for the exponential distribution: |
| + | :$$A_{X} \cdot\int_{0}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = A_{X} \cdot (-1/\lambda)\cdot\big [{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\big ]_{0}^{\infty} = A_{X} \cdot (1/\lambda) \stackrel{!}{=} 1 | ||
\hspace{0.3cm} \Rightarrow\hspace{0.3cm} A_{X} = \lambda \hspace{0.05cm}. $$ | \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A_{X} = \lambda \hspace{0.05cm}. $$ | ||
| − | |||
| − | |||
| − | + | '''(2)''' <u>Proposed solution 1</u> is correct: | |
| − | + | *From the graph on the information page, we can see that the height $A_Y$ of the Laplace PDF is only half as large as the maximum of the exponential PDF: | |
| − | + | :$$A_Y = \lambda/2.$$ | |
| − | $$ | + | |
| − | < | + | '''(3)''' Correct is <u>YES</u>, although for $z \ne 0$ always $f_X(z) = f_Y(z)$. Let us now consider the special case $z= 0$: |
| − | :* | + | * For the Laplace PDF: $f_Y(y = 0) = \lambda/2$. |
| − | $$m_1 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot \left [\frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\right ]_{0}^{\infty}= {1}/{\lambda} \hspace{0.05cm},$$ | + | * For the exponential PDF, the left-hand and right-hand limits differ for $x \to 0$. |
| − | + | *The PDF value at point $x= 0$ is the average of these two limits: | |
| − | $$m_2 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot | + | :$$f_X(0) = \frac{1}{2} \cdot \big [ 0 + \lambda \big] = \lambda/2 = f_Y(0)\hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | '''(4)''' <u>All proposed solutions</u> are correct. | ||
| + | |||
| + | For the exponential distribution, the $k$–th order moment is generally calculated to be | ||
| + | :$$m_k = \frac{k!}{\lambda^k} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} m_1 = \frac{1}{\lambda}, \hspace{0.3cm} m_2 = \frac{2}{\lambda^2}, \hspace{0.3cm} m_3 = \frac{6}{\lambda^3}, \ \text{...}$$ | ||
| + | Thus one obtains for | ||
| + | * the linear mean (first order moment): | ||
| + | :$$m_1 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot \left [\frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\right ]_{0}^{\infty}= {1}/{\lambda} \hspace{0.05cm},$$ | ||
| + | * the second order moment: | ||
| + | :$$m_2 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot | ||
(\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) | (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) | ||
\right ]_{0}^{\infty} ={2}/{\lambda^2} \hspace{0.05cm}.$$ | \right ]_{0}^{\infty} ={2}/{\lambda^2} \hspace{0.05cm}.$$ | ||
| − | + | From this, using Steiner's theorem for the variance of the exponential distribution, we get: | |
| − | $$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} -{1}/{\lambda^2} = {1}/{\lambda^2} | + | :$$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} -{1}/{\lambda^2} = {1}/{\lambda^2} |
\hspace{0.3cm} \Rightarrow\hspace{0.3cm} | \hspace{0.3cm} \Rightarrow\hspace{0.3cm} | ||
\sigma = {1}/{\lambda}\hspace{0.05cm}.$$ | \sigma = {1}/{\lambda}\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | ||
| − | $$m_2 = \frac{\lambda}{2} \cdot \int_{-\infty}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.1cm}{\rm d}y = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y = {2}/{\lambda^2} \hspace{0.05cm}.$$ | + | [[File:EN_Inf_A_4_3.png|right|frame|To illustrate the sample solution to problem '''(5)''']] |
| − | + | '''(5)''' Only the <u>proposed solution 2</u> is correct: | |
| − | $$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} - 0 ={2}/{\lambda^2} | + | *The second moment of "Laplace" is the same as for the exponential distribution because of the symmetric PDF: |
| + | :$$m_2 = \frac{\lambda}{2} \cdot \int_{-\infty}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.1cm}{\rm d}y = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y = {2}/{\lambda^2} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *In contrast, the mean of the Laplace distribution is $m_1 = 0$. | ||
| + | *Thus, the variance of the Laplace distribution is twice that of the exponential distribution: | ||
| + | :$$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} - 0 ={2}/{\lambda^2} | ||
\hspace{0.3cm} \Rightarrow\hspace{0.3cm} | \hspace{0.3cm} \Rightarrow\hspace{0.3cm} | ||
\sigma = {\sqrt{2}}/{\lambda}\hspace{0.05cm}.$$ | \sigma = {\sqrt{2}}/{\lambda}\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | '''(6)''' For the exponential distribution, according to the upper graph with $m_X = \sigma_X = 1/\lambda$: | |
| − | $${\rm Pr}( |X - m_X| > \sigma_X) = | + | :$${\rm Pr}( |X - m_X| > \sigma_X) \hspace{-0.05cm} = \hspace{-0.05cm} |
| − | {\rm Pr}( X > 2/\lambda) | + | {\rm Pr}( X > 2/\lambda) |
| − | = | + | \hspace{-0.05cm} = \hspace{-0.05cm} \lambda \cdot\int_{2/\lambda}^{\infty} \hspace{-0.08cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = |
-\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | -\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | ||
| − | \right ]_{2/\lambda}^{\infty} | + | \right ]_{2/\lambda}^{\infty} |
| − | = {\rm e}^{-2} \hspace{0.15cm}\underline {\approx 0.135 | + | = {\rm e}^{-2} \hspace{0.15cm}\underline {\approx 0.135}.$$ |
| − | + | For the Laplace distribution (lower graph), with $m_Y = 0$ and $\sigma_Y = \sqrt{2}/\lambda$ we obtain:: | |
| − | $${\rm Pr}( |Y - m_Y| > \sigma_Y) = | + | :$${\rm Pr}( |Y - m_Y| > \sigma_Y) = |
| − | 2 \cdot {\rm Pr}( Y > \sqrt{2}/\lambda) | + | 2 \cdot {\rm Pr}( Y > \sqrt{2}/\lambda) |
| − | = 2 \cdot \frac{\lambda}{2} \cdot\int_{\sqrt{2}/\lambda}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = | + | = 2 \cdot \frac{\lambda}{2} \cdot\int_{\sqrt{2}/\lambda}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x $$ |
| + | :$$\Rightarrow \hspace{0.3cm}{\rm Pr}( |Y - m_Y| > \sigma_Y) = | ||
\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | \left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} | ||
| − | \right ]_{\sqrt{2}/\lambda}^{\infty} | + | \right ]_{\sqrt{2}/\lambda}^{\infty} |
= - {\rm e}^{-\sqrt{2}} \hspace{0.15cm}\underline {\approx 0.243}\hspace{0.05cm}.$$ | = - {\rm e}^{-\sqrt{2}} \hspace{0.15cm}\underline {\approx 0.243}\hspace{0.05cm}.$$ | ||
| − | + | A comparison of the shaded areas in the accompanying graph qualitatively confirms the result: <br> ⇒ The blue areas together are slightly larger than the red area. | |
| + | |||
| + | |||
| Line 120: | Line 151: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.1 Differential Entropy^]] |
Latest revision as of 13:19, 18 January 2023
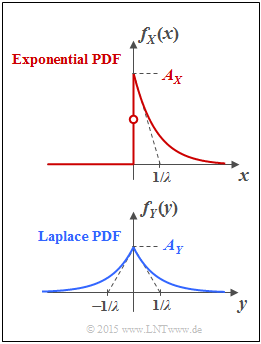
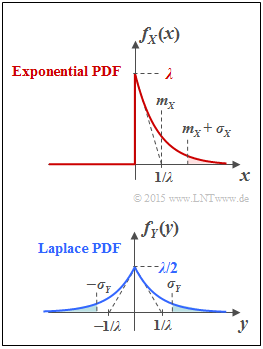
The upper graph shows the probability density function $\rm (PDF)$ of the exponential distribution:
- $$f_X(x) = \left\{ \begin{array}{c} A_{ X} \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm}x} \\ A_{ X}/2 \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm}x>0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x=0, \\ {\rm{f\ddot{u}r}} \hspace{0.1cm}x<0. \\ \end{array}$$
Drawn below is the PDF of the Laplace distribution, which can be specified for all $y$–values as follows:
- $$f_Y(y) = A_{ Y} \cdot {\rm e}^{-\lambda \hspace{0.05cm} \cdot \hspace{0.05cm} |\hspace{0.03cm}y\hspace{0.03cm}|}\hspace{0.05cm}.$$
The two continuous random variables $X$ and $Y$ are to be compared with respect to the following characteristics:
- The linear mean $m_1$ (first order moment),
- the second order moment ⇒ $m_2$,
- the variance $\sigma^2 = m_2 - m_1^2$ ⇒ Steiner's theorem,
- the standard deviation $\sigma$.
Hints:
- The task belongs to the chapter Differential Entropy.
- Useful hints for solving this task and further information on continuous random variables can be found in the third chapter "Continuous Random Variables" of the book Theory of Stochastic Signals.
- Also given are the two indefinite integrals:
- $$\int \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\hspace{0.05cm}, $$
- $$\int \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \hspace{0.05cm}. $$
Questions
Solution
- The area under the PDF must always be $1$ . It follows for the exponential distribution:
- $$A_{X} \cdot\int_{0}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = A_{X} \cdot (-1/\lambda)\cdot\big [{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\big ]_{0}^{\infty} = A_{X} \cdot (1/\lambda) \stackrel{!}{=} 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A_{X} = \lambda \hspace{0.05cm}. $$
(2) Proposed solution 1 is correct:
- From the graph on the information page, we can see that the height $A_Y$ of the Laplace PDF is only half as large as the maximum of the exponential PDF:
- $$A_Y = \lambda/2.$$
(3) Correct is YES, although for $z \ne 0$ always $f_X(z) = f_Y(z)$. Let us now consider the special case $z= 0$:
- For the Laplace PDF: $f_Y(y = 0) = \lambda/2$.
- For the exponential PDF, the left-hand and right-hand limits differ for $x \to 0$.
- The PDF value at point $x= 0$ is the average of these two limits:
- $$f_X(0) = \frac{1}{2} \cdot \big [ 0 + \lambda \big] = \lambda/2 = f_Y(0)\hspace{0.05cm}.$$
(4) All proposed solutions are correct.
For the exponential distribution, the $k$–th order moment is generally calculated to be
- $$m_k = \frac{k!}{\lambda^k} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} m_1 = \frac{1}{\lambda}, \hspace{0.3cm} m_2 = \frac{2}{\lambda^2}, \hspace{0.3cm} m_3 = \frac{6}{\lambda^3}, \ \text{...}$$
Thus one obtains for
- the linear mean (first order moment):
- $$m_1 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot \left [\frac{{\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}}{(-\lambda)^2}\cdot(-\lambda \cdot x-1)\right ]_{0}^{\infty}= {1}/{\lambda} \hspace{0.05cm},$$
- the second order moment:
- $$m_2 = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} x^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = \lambda \cdot\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\cdot (\frac{x^2}{-\lambda} - \frac{2x}{\lambda^2} + \frac{2}{\lambda^3}) \right ]_{0}^{\infty} ={2}/{\lambda^2} \hspace{0.05cm}.$$
From this, using Steiner's theorem for the variance of the exponential distribution, we get:
- $$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} -{1}/{\lambda^2} = {1}/{\lambda^2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \sigma = {1}/{\lambda}\hspace{0.05cm}.$$
(5) Only the proposed solution 2 is correct:
- The second moment of "Laplace" is the same as for the exponential distribution because of the symmetric PDF:
- $$m_2 = \frac{\lambda}{2} \cdot \int_{-\infty}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|y|}\hspace{0.1cm}{\rm d}y = \lambda \cdot\int_{0}^{\infty} \hspace{-0.01cm} y^2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y = {2}/{\lambda^2} \hspace{0.05cm}.$$
- In contrast, the mean of the Laplace distribution is $m_1 = 0$.
- Thus, the variance of the Laplace distribution is twice that of the exponential distribution:
- $$\sigma^2 = m_2 - m_1^2 = {2}/{\lambda^2} - 0 ={2}/{\lambda^2} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \sigma = {\sqrt{2}}/{\lambda}\hspace{0.05cm}.$$
(6) For the exponential distribution, according to the upper graph with $m_X = \sigma_X = 1/\lambda$:
- $${\rm Pr}( |X - m_X| > \sigma_X) \hspace{-0.05cm} = \hspace{-0.05cm} {\rm Pr}( X > 2/\lambda) \hspace{-0.05cm} = \hspace{-0.05cm} \lambda \cdot\int_{2/\lambda}^{\infty} \hspace{-0.08cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x = -\left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \right ]_{2/\lambda}^{\infty} = {\rm e}^{-2} \hspace{0.15cm}\underline {\approx 0.135}.$$
For the Laplace distribution (lower graph), with $m_Y = 0$ and $\sigma_Y = \sqrt{2}/\lambda$ we obtain::
- $${\rm Pr}( |Y - m_Y| > \sigma_Y) = 2 \cdot {\rm Pr}( Y > \sqrt{2}/\lambda) = 2 \cdot \frac{\lambda}{2} \cdot\int_{\sqrt{2}/\lambda}^{\infty} \hspace{-0.01cm} {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x $$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}( |Y - m_Y| > \sigma_Y) = \left [ {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \right ]_{\sqrt{2}/\lambda}^{\infty} = - {\rm e}^{-\sqrt{2}} \hspace{0.15cm}\underline {\approx 0.243}\hspace{0.05cm}.$$
A comparison of the shaded areas in the accompanying graph qualitatively confirms the result:
⇒ The blue areas together are slightly larger than the red area.