Difference between revisions of "Aufgaben:Exercise 3.3: Moments for Cosine-square PDF"
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Expected_Values_and_Moments |
}} | }} | ||
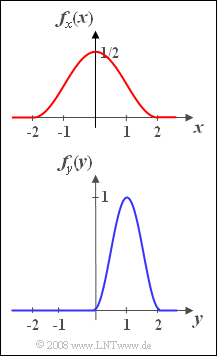
| − | [[File:P_ID119__Sto_A_3_3.png|right|frame| | + | [[File:P_ID119__Sto_A_3_3.png|right|frame|Squared cosine PDF <br>and a similar PDF]] |
| − | + | As in [[Aufgaben:Exercise_3.1:_cos²-PDF_and_PDF_with_Dirac_Functions|Exercise 3.1]] and [[Aufgaben:Exercise_3.2:_cos²-CDF_and_CDF_with_Step_Functions|Exercise 3. 2]] we consider the random variable restricted to the range of values from $-2$ to $+2$ with the following PDF in this section: | |
:$$f_x(x)= {1}/{2}\cdot \cos^2({\pi}/{4}\cdot { x}).$$ | :$$f_x(x)= {1}/{2}\cdot \cos^2({\pi}/{4}\cdot { x}).$$ | ||
| − | + | Next to this, we consider a second random variable $y$ that returns only values between $0$ and $2$ with the following PDF: | |
| − | :$$f_y(y)=\sin^2({\pi}/{2}\cdot | + | :$$f_y(y)=\sin^2({\pi}/{2}\cdot y).$$ |
| − | * | + | *Both probability density functions are shown in the graph. |
| − | * | + | *Outside the ranges $-2 < x < +2$ resp. $0 < x < +2$, the followings holds: $f_x(x) = 0$ resp. $f_y(y) = 0$. |
| − | * | + | *Both random variables can be taken as (normalized) instantaneous values of the associated random signals $x(t)$ or $y(t)$ resp. |
| Line 19: | Line 19: | ||
| − | + | Hints: | |
| − | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|Expected values and moments]]. | |
| − | |||
| − | |||
| − | * | ||
| − | * | + | *To solve this problem, you can use the following indefinite integral: |
:$$\int x^{2}\cdot {\cos}(ax)\,{\rm d}x=\frac{2 x}{ a^{ 2}}\cdot \cos(ax)+ \left [\frac{x^{\rm 2}}{\it a} - \frac{\rm 2}{\it a^{\rm 3}} \right ]\cdot \rm sin(\it ax \rm ) .$$ | :$$\int x^{2}\cdot {\cos}(ax)\,{\rm d}x=\frac{2 x}{ a^{ 2}}\cdot \cos(ax)+ \left [\frac{x^{\rm 2}}{\it a} - \frac{\rm 2}{\it a^{\rm 3}} \right ]\cdot \rm sin(\it ax \rm ) .$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true for any given PDF $f_x(x)$ ? Used are the following quantities: linear mean $m_1$, second moment $m_2$, variance $\sigma^2$. |
| − | |||
|type="[]"} | |type="[]"} | ||
| − | - $m_2 = 0$, | + | - $m_2 = 0$, if $m_1 \ne 0$. |
| − | - $m_2 = 0$, | + | - $m_2 = 0$, if $m_1 = 0$. |
| − | + $m_1 = 0$, | + | + $m_1 = 0$, if $m_2 = 0$. |
| − | + $m_2 > \sigma^2$, | + | + $m_2 > \sigma^2$, if $m_1 \ne 0$. |
| − | + $m_1 = 0$, | + | + $m_1 = 0$, if $f_x(-x) = f_x(x)$. |
| − | - $f_x(-x) = f_x(x)$, | + | - $f_x(-x) = f_x(x)$, if $m_1 = 0$. |
| − | { | + | {What is the DC component ("linear mean") of the signal $x(t)$? |
|type="{}"} | |type="{}"} | ||
$m_x \ = \ $ { 0. } | $m_x \ = \ $ { 0. } | ||
| − | { | + | {What is the standard deviation of the signal $x(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_x \ = | + | $\sigma_x \ = \ $ { 0.722 3% } |
| − | { | + | {The random variable $y$ can be derived from $x$. Which assignment is valid? |
|type="()"} | |type="()"} | ||
+ $y = 1+x/2.$ | + $y = 1+x/2.$ | ||
| Line 60: | Line 56: | ||
| − | { | + | {What is the DC component of the signal $y(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $m_y\ = | + | $m_y\ = $ { 1 3% } |
| − | { | + | {What is the standard deviation of the signal $y(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_y\ = | + | $\sigma_y\ = \ $ { 0.361 3% } |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Under all circumstances, <u>statements 3, 4, and 5</u> are correct: |
| − | * | + | *The first statement is never true, as is evident from the "Steiner's theorem". |
| − | * | + | *The second statement is only valid in the (trivial) special case $x = 0$. |
| − | + | However, there are also zero-mean random variables with asymmetric PDF. | |
| − | * | + | *This means: Statement 6 is not always true. |
| − | '''(2)''' | + | '''(2)''' Because of the PDF symmetry with respect to $x = 0$ it follows that for the linear mean $m_x \hspace{0.15cm}\underline{= 0}$. |
| − | '''(3)''' | + | '''(3)''' The standard deviation of the signal $x(t)$ is equal to the standard deviation $\sigma_x$ or equal to the root of the variance $\sigma_x^2$. |
| − | * | + | *Since the random variable $x$ has mean $m_x {= 0}$, the variance is equal to the second moment according to Steiner's theorem. |
| − | * | + | *This is also referred to as the power $($with respect to $1 \ \rm \Omega)$ in the context of signals. Thus: |
:$$\sigma_x^{\rm 2}=\int_{-\infty}^{+\infty}x^{\rm 2}\cdot f_x(x)\hspace{0.1cm}{\rm d}x=2 \cdot \int_{\rm 0}^{\rm 2} x^2/2 \cdot \cos^2({\pi}/4\cdot\it x)\hspace{0.1cm} {\rm d}x.$$ | :$$\sigma_x^{\rm 2}=\int_{-\infty}^{+\infty}x^{\rm 2}\cdot f_x(x)\hspace{0.1cm}{\rm d}x=2 \cdot \int_{\rm 0}^{\rm 2} x^2/2 \cdot \cos^2({\pi}/4\cdot\it x)\hspace{0.1cm} {\rm d}x.$$ | ||
| − | + | *With the relation $\cos^2(\alpha) = 0.5 \cdot \big[1 + \cos(2\alpha)\big]$ it follows: | |
| − | * | + | :$$\sigma_x^2=\int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{\rm 2} \hspace{0.1cm}{\rm d}x + \int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{2}\cdot \cos({\pi}/{\rm 2}\cdot\it x) \hspace{0.1cm} {\rm d}x.$$ |
| − | :$$\sigma_x^2=\int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{\rm 2} \hspace{0.1cm}{\rm d}x | + | *These two standard integrals can be found in tables. One obtains with $a = \pi/2$: |
| − | + | :$$\sigma_x^{\rm 2}=\left[\frac{x^{\rm 3}}{\rm 6} + \frac{x}{a^2}\cdot {\cos}(a x) + \left( \frac{x^{\rm2}}{{\rm2}a} - \frac{1}{a^3} \right) \cdot \sin(a \cdot x)\right]_{x=0}^{x=2} \hspace{0.5cm} | |
| − | * | + | \rightarrow \hspace{0.5cm} \sigma_{x}^{\rm 2}=\frac{\rm 4}{\rm 3}-\frac{\rm 8}{\rm \pi^2}\approx 0.524\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\sigma_x \hspace{0.15cm}\underline{\approx 0.722}.$$ |
| − | :$$\sigma_x^{\rm 2}=\left[\frac{x^{\rm 3}}{\rm 6} | ||
| − | \ | ||
| − | '''(4)''' | + | '''(4)''' Correct is the <u>first mentioned suggestion</u>: |
| − | * | + | *The variant $y = 2x$ would yield a random variable distributed between $-4$ and $+4$. |
| − | * | + | *In the last proposition $y = x/2-1$ the mean would be $m_y = -1$. |
| − | '''(5)''' | + | '''(5)''' From the graph on the specification sheet it is already obvious that $m_y \hspace{0.15cm}\underline{=+1}$ must hold. |
| − | '''(6)''' | + | '''(6)''' The mean value does not change the variance and rms. |
| − | * | + | *By compressing by the factor $2$ the standard deviation becomes smaller compared to subtask '''(3)''' also by this factor: |
:$$\sigma_y=\sigma_x/\rm 2\hspace{0.15cm}\underline{\approx 0.361}.$$ | :$$\sigma_y=\sigma_x/\rm 2\hspace{0.15cm}\underline{\approx 0.361}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:20, 18 January 2023
As in Exercise 3.1 and Exercise 3. 2 we consider the random variable restricted to the range of values from $-2$ to $+2$ with the following PDF in this section:
- $$f_x(x)= {1}/{2}\cdot \cos^2({\pi}/{4}\cdot { x}).$$
Next to this, we consider a second random variable $y$ that returns only values between $0$ and $2$ with the following PDF:
- $$f_y(y)=\sin^2({\pi}/{2}\cdot y).$$
- Both probability density functions are shown in the graph.
- Outside the ranges $-2 < x < +2$ resp. $0 < x < +2$, the followings holds: $f_x(x) = 0$ resp. $f_y(y) = 0$.
- Both random variables can be taken as (normalized) instantaneous values of the associated random signals $x(t)$ or $y(t)$ resp.
Hints:
- This exercise belongs to the chapter Expected values and moments.
- To solve this problem, you can use the following indefinite integral:
- $$\int x^{2}\cdot {\cos}(ax)\,{\rm d}x=\frac{2 x}{ a^{ 2}}\cdot \cos(ax)+ \left [\frac{x^{\rm 2}}{\it a} - \frac{\rm 2}{\it a^{\rm 3}} \right ]\cdot \rm sin(\it ax \rm ) .$$
Questions
Solution
- The first statement is never true, as is evident from the "Steiner's theorem".
- The second statement is only valid in the (trivial) special case $x = 0$.
However, there are also zero-mean random variables with asymmetric PDF.
- This means: Statement 6 is not always true.
(2) Because of the PDF symmetry with respect to $x = 0$ it follows that for the linear mean $m_x \hspace{0.15cm}\underline{= 0}$.
(3) The standard deviation of the signal $x(t)$ is equal to the standard deviation $\sigma_x$ or equal to the root of the variance $\sigma_x^2$.
- Since the random variable $x$ has mean $m_x {= 0}$, the variance is equal to the second moment according to Steiner's theorem.
- This is also referred to as the power $($with respect to $1 \ \rm \Omega)$ in the context of signals. Thus:
- $$\sigma_x^{\rm 2}=\int_{-\infty}^{+\infty}x^{\rm 2}\cdot f_x(x)\hspace{0.1cm}{\rm d}x=2 \cdot \int_{\rm 0}^{\rm 2} x^2/2 \cdot \cos^2({\pi}/4\cdot\it x)\hspace{0.1cm} {\rm d}x.$$
- With the relation $\cos^2(\alpha) = 0.5 \cdot \big[1 + \cos(2\alpha)\big]$ it follows:
- $$\sigma_x^2=\int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{\rm 2} \hspace{0.1cm}{\rm d}x + \int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{2}\cdot \cos({\pi}/{\rm 2}\cdot\it x) \hspace{0.1cm} {\rm d}x.$$
- These two standard integrals can be found in tables. One obtains with $a = \pi/2$:
- $$\sigma_x^{\rm 2}=\left[\frac{x^{\rm 3}}{\rm 6} + \frac{x}{a^2}\cdot {\cos}(a x) + \left( \frac{x^{\rm2}}{{\rm2}a} - \frac{1}{a^3} \right) \cdot \sin(a \cdot x)\right]_{x=0}^{x=2} \hspace{0.5cm} \rightarrow \hspace{0.5cm} \sigma_{x}^{\rm 2}=\frac{\rm 4}{\rm 3}-\frac{\rm 8}{\rm \pi^2}\approx 0.524\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\sigma_x \hspace{0.15cm}\underline{\approx 0.722}.$$
(4) Correct is the first mentioned suggestion:
- The variant $y = 2x$ would yield a random variable distributed between $-4$ and $+4$.
- In the last proposition $y = x/2-1$ the mean would be $m_y = -1$.
(5) From the graph on the specification sheet it is already obvious that $m_y \hspace{0.15cm}\underline{=+1}$ must hold.
(6) The mean value does not change the variance and rms.
- By compressing by the factor $2$ the standard deviation becomes smaller compared to subtask (3) also by this factor:
- $$\sigma_y=\sigma_x/\rm 2\hspace{0.15cm}\underline{\approx 0.361}.$$