Difference between revisions of "Aufgaben:Exercise 2.2: Multi-Level Signals"
From LNTwww
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/From_Random_Experiment_to_Random_Variable |
}} | }} | ||
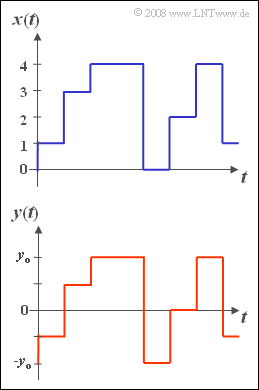
| − | [[File:P_ID85__Sto_A_2_2.png|right|frame|Two similar | + | [[File:P_ID85__Sto_A_2_2.png|right|frame|Two similar multi-level signals]] |
| − | Let the | + | Let the rectangular signal $x(t)$ be dimensionless and can only have the current values $0, \ 1, \ 2, \ \text{...} \ , \ M-2, \ M-1$ with equal probability. The upper graph shows this signal for the special case $M = 5$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The rectangular zero mean signal $y(t)$ can also assume $M$ different values. | ||
| + | *It is restricted to the range from $ -y_0 \le y \le +y_0$. | ||
| + | *In the graph below you can see the signal $y(t)$, again for the level number $M = 5$. | ||
| Line 23: | Line 19: | ||
Hints: | Hints: | ||
*The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Momente_einer_diskreten_Zufallsgröße|Moments of a Discrete Random Variable]]. | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Momente_einer_diskreten_Zufallsgröße|Moments of a Discrete Random Variable]]. | ||
| − | + | *Fur numerical calculations, use $y_0 = \rm 2\hspace{0.05cm}V$. | |
| − | + | *The topic of this chapter is illustrated with examples in the (German language) learning video<br> [[Momentenberechnung_bei_diskreten_Zufallsgrößen_(Lernvideo)|"Momentenberechnung bei diskreten Zufallsgrößen"]] ⇒ "Calculating Moments for Discrete-Valued Random Variables" | |
| − | + | ||
| Line 49: | Line 45: | ||
| − | {What is the variance $\sigma_y^2$ of the random variable $y$? Consider the result from '''(2)'''. | + | {What is the variance $\sigma_y^2$ of the random variable $y$ in general and for $M= 5$? Consider the result from '''(2)'''. |
|type="{}"} | |type="{}"} | ||
$\sigma_y^2\ = \ $ { 2 3% } $\ \rm V^2$ | $\sigma_y^2\ = \ $ { 2 3% } $\ \rm V^2$ | ||
| Line 60: | Line 56: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''(1)''' One obtains by averaging over all possible signal values for the linear mean: | '''(1)''' One obtains by averaging over all possible signal values for the linear mean: | ||
| Line 101: | Line 64: | ||
| − | '''(2)''' Analogously | + | '''(2)''' Analogously to '''(1)''' one obtains for the second moment (second order moment): |
: $$m_{\rm 2\it x}= \rm \sum_{\mu=0}^{\it M -\rm 1}\it p_\mu\cdot x_{\mu}^{\rm 2}=\frac{\rm 1}{\it M}\cdot \sum_{\mu=\rm 0}^{\rm M- 1}\mu^{\rm 2} = \frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M\cdot(\rm 2\it M-\rm 1)}{\rm 6} = \frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}. $$ | : $$m_{\rm 2\it x}= \rm \sum_{\mu=0}^{\it M -\rm 1}\it p_\mu\cdot x_{\mu}^{\rm 2}=\frac{\rm 1}{\it M}\cdot \sum_{\mu=\rm 0}^{\rm M- 1}\mu^{\rm 2} = \frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M\cdot(\rm 2\it M-\rm 1)}{\rm 6} = \frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}. $$ | ||
| − | *In the special case $M= 5$ the | + | *In the special case $M= 5$ the second moment $m_{2x} {=6}$. |
*From this, the variance can be calculated using Steiner's theorem: | *From this, the variance can be calculated using Steiner's theorem: | ||
:$$\sigma_x^{\rm 2}=m_{\rm 2\it x}-m_x^{\rm 2}=\frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}-\frac{(\it M-\rm 1)^{\rm 2}}{\rm 4}=\frac{\it M^{\rm 2}-\rm 1}{\rm 12}.$$ | :$$\sigma_x^{\rm 2}=m_{\rm 2\it x}-m_x^{\rm 2}=\frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}-\frac{(\it M-\rm 1)^{\rm 2}}{\rm 4}=\frac{\it M^{\rm 2}-\rm 1}{\rm 12}.$$ | ||
| Line 112: | Line 75: | ||
| − | '''(3)''' Because of the symmetry of $y$ | + | '''(3)''' Because of the symmetry of $y$, it holds independently of $M$: |
| − | :$$ | + | :$$m_y \;\underline{= 0}.$$ |
| − | |||
| − | '''(4)''' | + | '''(4)''' The following relation holds between $x(t)$ and $y(t)$: |
:$$y(t)=\frac{2\cdot y_{\rm 0}}{M-\rm 1}\cdot \big[x(t)-m_x\big].$$ | :$$y(t)=\frac{2\cdot y_{\rm 0}}{M-\rm 1}\cdot \big[x(t)-m_x\big].$$ | ||
Latest revision as of 13:20, 18 January 2023
Let the rectangular signal $x(t)$ be dimensionless and can only have the current values $0, \ 1, \ 2, \ \text{...} \ , \ M-2, \ M-1$ with equal probability. The upper graph shows this signal for the special case $M = 5$.
The rectangular zero mean signal $y(t)$ can also assume $M$ different values.
- It is restricted to the range from $ -y_0 \le y \le +y_0$.
- In the graph below you can see the signal $y(t)$, again for the level number $M = 5$.
Hints:
- The exercise belongs to the chapter Moments of a Discrete Random Variable.
- Fur numerical calculations, use $y_0 = \rm 2\hspace{0.05cm}V$.
- The topic of this chapter is illustrated with examples in the (German language) learning video
"Momentenberechnung bei diskreten Zufallsgrößen" ⇒ "Calculating Moments for Discrete-Valued Random Variables"
Questions
Solution
(1) One obtains by averaging over all possible signal values for the linear mean:
- $$m_{\it x}=\rm \sum_{\mu=0}^{\it M-{\rm 1}} \it p_\mu\cdot x_{\mu}=\frac{\rm 1}{\it M} \cdot \sum_{\mu=\rm 0}^{\it M-\rm 1}\mu=\frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M}{\rm 2}=\frac{\it M-\rm 1}{\rm 2}.$$
- In the special case $M= 5$ the linear mean results in $m_x \;\underline{= 2}$.
(2) Analogously to (1) one obtains for the second moment (second order moment):
- $$m_{\rm 2\it x}= \rm \sum_{\mu=0}^{\it M -\rm 1}\it p_\mu\cdot x_{\mu}^{\rm 2}=\frac{\rm 1}{\it M}\cdot \sum_{\mu=\rm 0}^{\rm M- 1}\mu^{\rm 2} = \frac{\rm 1}{\it M}\cdot\frac{(\it M-\rm 1)\cdot \it M\cdot(\rm 2\it M-\rm 1)}{\rm 6} = \frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}. $$
- In the special case $M= 5$ the second moment $m_{2x} {=6}$.
- From this, the variance can be calculated using Steiner's theorem:
- $$\sigma_x^{\rm 2}=m_{\rm 2\it x}-m_x^{\rm 2}=\frac{(\it M-\rm 1)\cdot(\rm 2\it M-\rm 1)}{\rm 6}-\frac{(\it M-\rm 1)^{\rm 2}}{\rm 4}=\frac{\it M^{\rm 2}-\rm 1}{\rm 12}.$$
- In the special case $M= 5$ the result for the variance $\sigma_x^2 \;\underline{= 2}$.
(3) Because of the symmetry of $y$, it holds independently of $M$:
- $$m_y \;\underline{= 0}.$$
(4) The following relation holds between $x(t)$ and $y(t)$:
- $$y(t)=\frac{2\cdot y_{\rm 0}}{M-\rm 1}\cdot \big[x(t)-m_x\big].$$
- From this it follows for the variances:
- $$\sigma_y^{\rm 2}=\frac{4\cdot y_{\rm 0}^{\rm 2}}{( M - 1)^{\rm 2}}\cdot \sigma_x^{\rm 2}=\frac{y_{\rm 0}^{\rm 2}\cdot (M^{\rm 2}- 1)}{3\cdot (M- 1)^{\rm 2}}=\frac{y_{\rm 0}^{\rm 2}\cdot ( M+ 1)}{ 3\cdot ( M- 1)}. $$
- In the special case $M= 5$ this results in:
- $$\it \sigma_y^{\rm 2}= \frac {\it y_{\rm 0}^{\rm 2} \cdot {\rm 6}}{\rm 3 \cdot 4}\hspace{0.15cm} \underline{=\rm2\,V^{2}}.$$