Difference between revisions of "Aufgaben:Exercise 2.5Z: Square Wave"
m (Text replacement - "Signal_Representation/Fourierreihe" to "Signal_Representation/Fourier_Series") |
|||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fourier_Series |
}} | }} | ||
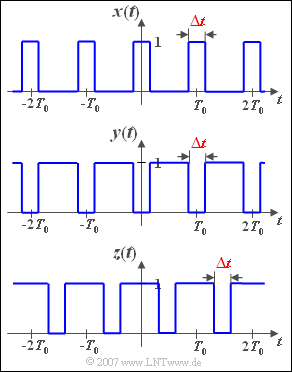
| − | [[File:P_ID323__Sig_Z_2_5.png|right|frame| | + | [[File:P_ID323__Sig_Z_2_5.png|right|frame|Various square wave signals]] |
| − | + | The signal $x(t)$ periodic with time $T_0$ is described by the single parameter $\Delta t$; | |
| + | let the amplitude of the square-wave pulses be $1$ in each case. Since $x(t)$ is even, all sine coefficients $B_n = 0$. | ||
| − | + | The DC signal coefficient is $A_0 = \Delta t/T_0$ and the following applies to the cosine coefficients: | |
:$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$ | :$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$ | ||
| − | In | + | In subtasks '''(1)''' and '''(2)''' the signal $x(t)$ is analyzed for the two parameter values $\Delta t/T_0 = 0.5$ and $\Delta t/T_0 = 0.25$ respectively. |
| − | + | Then we consider the two signals $y(t)$ and $z(t)$, each with $\Delta t/T_0 = 0.25$. There is a fixed relationship between these signals and $x(t)$ which can be exploited for the calculation. | |
| Line 18: | Line 19: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Series|Fourier Series]]. |
| − | * | + | *You can find a compact summary of the topic in the two learning videos |
| − | + | :[[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] ⇒ "To calculate the Fourier coefficients", | |
| − | + | : [[Eigenschaften_der_Fourierreihendarstellung_(Lernvideo)|Eigenschaften der Fourierreihendarstellung]] ⇒ "Properties of the Fourier series representation". | |
| Line 28: | Line 29: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true for the signal $x(t)$ with $\Delta t/T_0 = 0.5$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The spectral function ${X(f)}$ contains a Dirac delta function at $f = 0$ with the weight $0.5$. |
| − | - | + | - The spectral function ${X(f)}$ contains Dirac delta lines at all multiples of the base frequency $f_0 = 1/T_0$. |
| − | + | + | + The spectral function ${X(f)}$ contains Dirac delta lines at odd multiples of the base frequency $f_0$. |
| − | - | + | - The spectral line at $f_0$ has the weight $2/\pi = 0.636$. |
| − | + | + | + The spectral line at $–\hspace{-0.1cm}f_0$ has the weight $1/\pi = 0.318$. |
| − | { | + | {Which statements are true for the signal $x(t)$ with $\Delta t/T_0 = 0.25$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The spectral function ${X(f)}$ contains Dirac delta lines at all odd multiples of the base frequency $f_0$. |
| − | + ${X(f)}$ | + | + ${X(f)}$ has Dirac delta lines at $\pm2f_0$, $\pm6f_0$, $\pm10f_0$, etc. |
| − | - ${X(f)}$ | + | - ${X(f)}$ has Dirac delta lines at $\pm4f_0$, $\pm8f_0$, $\pm12f_0$, etc. |
| − | + | + | + The Dirac delta line at $2f_0$ has the weight $1/(2\pi) = 0.159$. |
| − | { | + | {What is the DC coefficient of the signal ${y(t)}$? |
|type="{}"} | |type="{}"} | ||
$y(t)$: $A_0 \ = \ $ { 0.75 3% } | $y(t)$: $A_0 \ = \ $ { 0.75 3% } | ||
| − | { | + | {What is the relationship between the signals $x(t)$ and ${y(t)}$? With the help of these considerations, give the Fourier coefficients of ${y(t)}$. <br>What are the coefficients $A_1$ and $A_2$ of this signal? |
|type="{}"} | |type="{}"} | ||
$y(t)$: $A_1\ = \ $ { -0.46--0.44 } | $y(t)$: $A_1\ = \ $ { -0.46--0.44 } | ||
| Line 59: | Line 60: | ||
| − | { | + | {What is the relationship between the signals ${y(t)}$ and ${z(t)}$? What are the coefficients $A_1$ and $A_2$ of the signal ${z(t)}$? <br>Check the result using the given coefficients of the signal $x(t)$. |
|type="{}"} | |type="{}"} | ||
$z(t)$: $A_1 \ = \ $ { 0.45 3% } | $z(t)$: $A_1 \ = \ $ { 0.45 3% } | ||
| Line 68: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Statements 1, 3 and 5</u> are correct: |
| − | * | + | *The spectral function contains a Dirac delta line at $f = 0$ with weight $0.5$ (DC component) as well as further spectral lines at odd multiples ($n = \pm1, \pm3, \pm5,\text{...}$ of $f_0$. |
| − | * | + | *The weights at $\pm f_0$ are $A_1/2 = 1/\pi = 0.318$ in each case. |
| − | '''(2)''' | + | '''(2)''' <u>Statements 1, 2 and 4</u> are correct: |
| − | * | + | *Spectral lines exist at all odd multiples of the basic frequency, and additionally at the $2–{\rm fold}$, $6–{\rm fold}$ and $10–{\rm fold}$. |
| − | * | + | *For example $A_1 = 1/\pi = 0.450$. The Dirac delta line at $2f_0$ thus has the weight $A_2/2 = 1/(2\pi) = 0.159$. |
| − | * | + | *For $n = 4$, $n = 8$, etc., on the other hand, the coefficients $A_n = 0$, since the following holds for the sine function: $\sin(\pi) = \sin(2\pi) =\text{ ...} = 0$. |
| − | '''(3)''' | + | '''(3)''' From the graphical representation of the signal ${y(t)}$ it is clear that $A_0 = 0.75$ must apply. The same result can be obtained using the relationship: |
:$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$ | :$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$ | ||
| − | '''(4)''' | + | '''(4)''' The following applies: ${y(t)} = 1 - x(t)$. For $n \neq 0$ the Fourier coefficients are the same as for the signal $x(t)$, but with negative signs. In particular: |
:$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$ | :$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$ | ||
:$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$ | :$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$ | ||
| − | '''(5)''' | + | '''(5)''' ${z(t)} = y(t - T_0/2)$ applies. With the Fourier series representation of ${y(t)}$ it follows: |
:$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$ | :$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$ | ||
:$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\text{...}$$ | :$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\text{...}$$ | ||
| − | + | Thus one obtains: | |
:$$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$ | :$$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$ | ||
| − | + | The same result is obtained starting from the given coefficients with $\Delta t/T_0 = 0.75$: | |
:$$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, | :$$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, | ||
\hspace {0.5cm}A_2^{(z)}= | \hspace {0.5cm}A_2^{(z)}= | ||
| Line 104: | Line 105: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^2.4 Fourier Series^]] |
Latest revision as of 13:30, 18 January 2023
The signal $x(t)$ periodic with time $T_0$ is described by the single parameter $\Delta t$; let the amplitude of the square-wave pulses be $1$ in each case. Since $x(t)$ is even, all sine coefficients $B_n = 0$.
The DC signal coefficient is $A_0 = \Delta t/T_0$ and the following applies to the cosine coefficients:
- $$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$
In subtasks (1) and (2) the signal $x(t)$ is analyzed for the two parameter values $\Delta t/T_0 = 0.5$ and $\Delta t/T_0 = 0.25$ respectively.
Then we consider the two signals $y(t)$ and $z(t)$, each with $\Delta t/T_0 = 0.25$. There is a fixed relationship between these signals and $x(t)$ which can be exploited for the calculation.
Hints:
- This exercise belongs to the chapter Fourier Series.
- You can find a compact summary of the topic in the two learning videos
- Zur Berechnung der Fourierkoeffizienten ⇒ "To calculate the Fourier coefficients",
- Eigenschaften der Fourierreihendarstellung ⇒ "Properties of the Fourier series representation".
Questions
Solution
- The spectral function contains a Dirac delta line at $f = 0$ with weight $0.5$ (DC component) as well as further spectral lines at odd multiples ($n = \pm1, \pm3, \pm5,\text{...}$ of $f_0$.
- The weights at $\pm f_0$ are $A_1/2 = 1/\pi = 0.318$ in each case.
(2) Statements 1, 2 and 4 are correct:
- Spectral lines exist at all odd multiples of the basic frequency, and additionally at the $2–{\rm fold}$, $6–{\rm fold}$ and $10–{\rm fold}$.
- For example $A_1 = 1/\pi = 0.450$. The Dirac delta line at $2f_0$ thus has the weight $A_2/2 = 1/(2\pi) = 0.159$.
- For $n = 4$, $n = 8$, etc., on the other hand, the coefficients $A_n = 0$, since the following holds for the sine function: $\sin(\pi) = \sin(2\pi) =\text{ ...} = 0$.
(3) From the graphical representation of the signal ${y(t)}$ it is clear that $A_0 = 0.75$ must apply. The same result can be obtained using the relationship:
- $$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$
(4) The following applies: ${y(t)} = 1 - x(t)$. For $n \neq 0$ the Fourier coefficients are the same as for the signal $x(t)$, but with negative signs. In particular:
- $$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$
- $$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$
(5) ${z(t)} = y(t - T_0/2)$ applies. With the Fourier series representation of ${y(t)}$ it follows:
- $$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$
- $$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\text{...}$$
Thus one obtains:
- $$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$
The same result is obtained starting from the given coefficients with $\Delta t/T_0 = 0.75$:
- $$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, \hspace {0.5cm}A_2^{(z)}= {1}/{\pi} \cdot \sin({3}/{2} \cdot \pi) =-{1}/{\pi}.$$