Difference between revisions of "Aufgaben:Exercise 3.8: Modulation Index and Bandwidth"
From LNTwww
| (13 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Frequency_Modulation_(FM) |
}} | }} | ||
| − | [[File:P_ID1105__Mod_A_3_7.png|right|frame| | + | [[File:P_ID1105__Mod_A_3_7.png|right|frame|Bessel function values]] |
| − | + | A harmonic oscillation of the form | |
:$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$ | :$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$ | ||
| − | + | is angle-modulated and then the one-sided magnitude spectrum $|S_+(f)|$ is obtained. | |
| − | * | + | *with a message frequency of $f_{\rm N} = 2 \ \rm kHz$ the following spectral lines can be seen with the following weights: |
:$$|S_{\rm +}(98\,{\rm kHz})| = |S_{\rm +}(102\,{\rm kHz})| = 1.560\,{\rm V}\hspace{0.05cm},$$ $$|S_{\rm +}(96\,{\rm kHz})| = |S_{\rm +}(104\,{\rm kHz})| = 1.293\,{\rm V}\hspace{0.05cm},$$ | :$$|S_{\rm +}(98\,{\rm kHz})| = |S_{\rm +}(102\,{\rm kHz})| = 1.560\,{\rm V}\hspace{0.05cm},$$ $$|S_{\rm +}(96\,{\rm kHz})| = |S_{\rm +}(104\,{\rm kHz})| = 1.293\,{\rm V}\hspace{0.05cm},$$ | ||
:$$ |S_{\rm +}(94\,{\rm kHz})| = |S_{\rm +}(106\,{\rm kHz})| = 0.594\,{\rm V}\hspace{0.05cm}.$$ | :$$ |S_{\rm +}(94\,{\rm kHz})| = |S_{\rm +}(106\,{\rm kHz})| = 0.594\,{\rm V}\hspace{0.05cm}.$$ | ||
| − | : | + | :Further spectral lines follow each with frequency spacing $f_{\rm N} = 2 \ \rm kHz$, but are not given here and can be ignored. |
| − | * | + | *If one increases the message frequency to $f_{\rm N} = 4 \ \rm kHz$, there occur dominant lines |
:$$|S_{\rm +}(100\,{\rm kHz})| = 2.013\,{\rm V}\hspace{0.05cm},$$ | :$$|S_{\rm +}(100\,{\rm kHz})| = 2.013\,{\rm V}\hspace{0.05cm},$$ | ||
:$$|S_{\rm +}(96\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(104\,{\rm kHz})| = 1.494\,{\rm V}\hspace{0.05cm},$$ | :$$|S_{\rm +}(96\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(104\,{\rm kHz})| = 1.494\,{\rm V}\hspace{0.05cm},$$ | ||
:$$ |S_{\rm +}(92\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(108\,{\rm kHz})| = 0.477\,{\rm V},$$ | :$$ |S_{\rm +}(92\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(108\,{\rm kHz})| = 0.477\,{\rm V},$$ | ||
| − | : | + | :as well as further, negligible Dirac delta lines with spacing $f_{\rm N} = 4 \ \rm kHz$. |
| Line 26: | Line 26: | ||
| − | + | ''Hints:'' | |
| − | '' | + | *This exercise belongs to the chapter [[Modulation_Methods/Frequency_Modulation_(FM)|Frequency Modulation]]. |
| − | * | + | *Reference is also made to the chapter [[Modulation_Methods/Phase_Modulation_(PM)|Phase Modulation]] and particularly to the section [[Modulation_Methods/Frequency_Modulation_(FM)#Signal_characteristics_with_frequency_modulation|Signal characteristics with frequency modulation]]. |
| − | * | + | |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which modulation method is used here? |
|type="()"} | |type="()"} | ||
| − | - | + | - Phase modulation. |
| − | + | + | + Frequency modulation. |
| − | { | + | {What is the modulation index $η_2$ at message frequency $f_{\rm N} = 2 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$η_2 \ = \ $ { 2.4 3% } | $η_2 \ = \ $ { 2.4 3% } | ||
| − | { | + | {What is the carrier amplitude? |
|type="{}"} | |type="{}"} | ||
$A_{\rm T} \ = \ $ { 3 3% } $\ \rm V$ | $A_{\rm T} \ = \ $ { 3 3% } $\ \rm V$ | ||
| − | { | + | {Specify the bandwidth $B_2$ for $f_{\rm N} = 2 \ \rm kHz$ if a distortion factor $K < 1\%$ is desired. |
|type="{}"} | |type="{}"} | ||
$B_2 \ = \ $ { 17.6 3% } $\ \rm kHz$ | $B_2 \ = \ $ { 17.6 3% } $\ \rm kHz$ | ||
| − | { | + | {What is the modulation index $η_4$ at message frequency $f_{\rm N} = 4 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$η_4\ = \ $ { 1.2 3% } | $η_4\ = \ $ { 1.2 3% } | ||
| − | { | + | {What channel bandwidth $B_4$ is now required to ensure $K < 1\%$ ? |
|type="{}"} | |type="{}"} | ||
$B_4 \ = \ $ { 25.6 3% } $\ \rm kHz$ | $B_4 \ = \ $ { 25.6 3% } $\ \rm kHz$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' We are dealing with a frequency modulation⇒ <u>Answer 2</u>. |
| − | * | + | *In phase modulation, the weights of the Dirac delta lines would not change when the frequency is doubled. |
| − | '''(2)''' | + | '''(2)''' The spectral function given suggests the carrier frequency $f_{\rm T} = 100 \ \rm kHz$ due to the symmetry properties. |
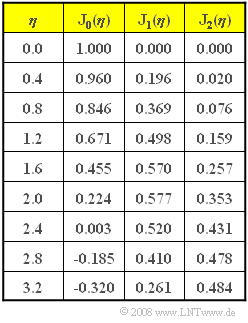
| + | *Since at $f_{\rm N} = 2 \ \rm kHz$ the spectral line disappears at $f_{\rm T} = 100 \ \rm kHz$ , we can assume $η_2 \hspace{0.15cm}\underline { ≈ 2.4}$ . | ||
| + | *A check of the other pulse weights confirms this result: | ||
:$$\frac { |S_{\rm +}(f =102\,{\rm kHz})|}{ |S_{\rm +}(f =104\,{\rm kHz})|} = 1.206,\hspace{0.2cm} \frac { {\rm J}_1(2.4)}{ {\rm J}_2(2.4)}= 1.206 \hspace{0.05cm}.$$ | :$$\frac { |S_{\rm +}(f =102\,{\rm kHz})|}{ |S_{\rm +}(f =104\,{\rm kHz})|} = 1.206,\hspace{0.2cm} \frac { {\rm J}_1(2.4)}{ {\rm J}_2(2.4)}= 1.206 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' | + | '''(3)''' The weights of the Dirac delta lines at $f_{\rm T} + n · f_{\rm N}$ are generally: |
| + | :$$D_n = A_{\rm T} \cdot { {\rm J}_n(\eta)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} D_1 = A_{\rm T} \cdot { {\rm J}_1(\eta)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A_{\rm T} = D_1/{\rm J}_1(η) = 1.560\ \rm V/0.520\hspace{0.15cm}\underline { = 3 \ V}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Given the requirement $K < 1\%$ , one can use the following rule of thumb (''Carson's rule''): | ||
:$$B_{\rm 2} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.15cm}\underline {= 17.6\,{\rm kHz}}\hspace{0.05cm}.$$ | :$$B_{\rm 2} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.15cm}\underline {= 17.6\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| − | + | *Thus, the Fourier coefficients $D_{–4}$, ... , $D_4$ are available. | |
| − | '''(5)''' | + | |
| + | '''(5)''' For frequency modulation, the general rule is: | ||
:$$\eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.05cm}.$$ | :$$\eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.05cm}.$$ | ||
| − | + | *Thus, by doubling the message frequency $f_{\rm N}$, the modulation index is halved: $η_4 = η_2/2\hspace{0.15cm}\underline { = 1.2}$. | |
| + | |||
| − | '''(6)''' | + | '''(6)''' Using the same calculation as in question '''(4)''' , the channel bandwidth necessary for $K < 1\%$ is obtained using |
:$$B_4 = 3.2 · 8\ \rm kHz \hspace{0.15cm}\underline {= 25.6 \ \rm kHz}.$$ | :$$B_4 = 3.2 · 8\ \rm kHz \hspace{0.15cm}\underline {= 25.6 \ \rm kHz}.$$ | ||
| − | + | *Because the modulation index is only half as large, transmitting the Fourier coefficients $D_{–3}$, ... , $D_3$ is sufficient for limiting the distortion factor to $1\%$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 96: | Line 102: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^3.2 Frequency Modulation^]] |
Latest revision as of 15:22, 18 January 2023
A harmonic oscillation of the form
- $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$
is angle-modulated and then the one-sided magnitude spectrum $|S_+(f)|$ is obtained.
- with a message frequency of $f_{\rm N} = 2 \ \rm kHz$ the following spectral lines can be seen with the following weights:
- $$|S_{\rm +}(98\,{\rm kHz})| = |S_{\rm +}(102\,{\rm kHz})| = 1.560\,{\rm V}\hspace{0.05cm},$$ $$|S_{\rm +}(96\,{\rm kHz})| = |S_{\rm +}(104\,{\rm kHz})| = 1.293\,{\rm V}\hspace{0.05cm},$$
- $$ |S_{\rm +}(94\,{\rm kHz})| = |S_{\rm +}(106\,{\rm kHz})| = 0.594\,{\rm V}\hspace{0.05cm}.$$
- Further spectral lines follow each with frequency spacing $f_{\rm N} = 2 \ \rm kHz$, but are not given here and can be ignored.
- If one increases the message frequency to $f_{\rm N} = 4 \ \rm kHz$, there occur dominant lines
- $$|S_{\rm +}(100\,{\rm kHz})| = 2.013\,{\rm V}\hspace{0.05cm},$$
- $$|S_{\rm +}(96\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(104\,{\rm kHz})| = 1.494\,{\rm V}\hspace{0.05cm},$$
- $$ |S_{\rm +}(92\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(108\,{\rm kHz})| = 0.477\,{\rm V},$$
- as well as further, negligible Dirac delta lines with spacing $f_{\rm N} = 4 \ \rm kHz$.
Hints:
- This exercise belongs to the chapter Frequency Modulation.
- Reference is also made to the chapter Phase Modulation and particularly to the section Signal characteristics with frequency modulation.
Questions
Solution
(1) We are dealing with a frequency modulation⇒ Answer 2.
- In phase modulation, the weights of the Dirac delta lines would not change when the frequency is doubled.
(2) The spectral function given suggests the carrier frequency $f_{\rm T} = 100 \ \rm kHz$ due to the symmetry properties.
- Since at $f_{\rm N} = 2 \ \rm kHz$ the spectral line disappears at $f_{\rm T} = 100 \ \rm kHz$ , we can assume $η_2 \hspace{0.15cm}\underline { ≈ 2.4}$ .
- A check of the other pulse weights confirms this result:
- $$\frac { |S_{\rm +}(f =102\,{\rm kHz})|}{ |S_{\rm +}(f =104\,{\rm kHz})|} = 1.206,\hspace{0.2cm} \frac { {\rm J}_1(2.4)}{ {\rm J}_2(2.4)}= 1.206 \hspace{0.05cm}.$$
(3) The weights of the Dirac delta lines at $f_{\rm T} + n · f_{\rm N}$ are generally:
- $$D_n = A_{\rm T} \cdot { {\rm J}_n(\eta)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} D_1 = A_{\rm T} \cdot { {\rm J}_1(\eta)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A_{\rm T} = D_1/{\rm J}_1(η) = 1.560\ \rm V/0.520\hspace{0.15cm}\underline { = 3 \ V}.$$
(4) Given the requirement $K < 1\%$ , one can use the following rule of thumb (Carson's rule):
- $$B_{\rm 2} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.15cm}\underline {= 17.6\,{\rm kHz}}\hspace{0.05cm}.$$
- Thus, the Fourier coefficients $D_{–4}$, ... , $D_4$ are available.
(5) For frequency modulation, the general rule is:
- $$\eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.05cm}.$$
- Thus, by doubling the message frequency $f_{\rm N}$, the modulation index is halved: $η_4 = η_2/2\hspace{0.15cm}\underline { = 1.2}$.
(6) Using the same calculation as in question (4) , the channel bandwidth necessary for $K < 1\%$ is obtained using
- $$B_4 = 3.2 · 8\ \rm kHz \hspace{0.15cm}\underline {= 25.6 \ \rm kHz}.$$
- Because the modulation index is only half as large, transmitting the Fourier coefficients $D_{–3}$, ... , $D_3$ is sufficient for limiting the distortion factor to $1\%$.