Difference between revisions of "Aufgaben:Exercise 1.2: ISDN and PCM"
| (2 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:EN_Bei_A_1_2.png|right|frame|Components of PCM transmitter | + | [[File:EN_Bei_A_1_2.png|right|frame|Components of PCM transmitter]] |
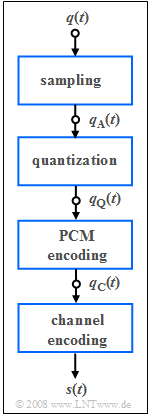
| − | The conversion of the analog | + | The conversion of the analog speech signal $q(t)$ into the binary signal $q_{\rm C}(t)$ is done at $\rm ISDN$ ("Integrated Services Digital Network") according to the guidelines of "pulse code modulation" $\rm (PCM)$ by |
*sampling in the interval $T_{\rm A} = 1/f_{\rm A}$, | *sampling in the interval $T_{\rm A} = 1/f_{\rm A}$, | ||
| Line 86: | Line 86: | ||
:$$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$ | :$$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$ | ||
| − | *With larger noise interference, $\rho_{v}$ can further (significantly) reduced by the transmission errors. | + | *With larger noise interference, $\rho_{v}$ can further (significantly) be reduced by the transmission errors. |
*In contrast, sampling results in no loss of quality if the sampling theorem is obeyed. | *In contrast, sampling results in no loss of quality if the sampling theorem is obeyed. | ||
Latest revision as of 16:36, 23 January 2023
The conversion of the analog speech signal $q(t)$ into the binary signal $q_{\rm C}(t)$ is done at $\rm ISDN$ ("Integrated Services Digital Network") according to the guidelines of "pulse code modulation" $\rm (PCM)$ by
- sampling in the interval $T_{\rm A} = 1/f_{\rm A}$,
- quantization to $M = 256$ discrete values,
- binary PCM encoding with $N$ bits per quantization value.
The net data rate of a $\rm B$ channel ("Bearer Channel") is $64 \ \rm kbit/s$ and corresponds to the bit rate of the redundancy-free binary signal $q_{\rm C}(t)$.
However, because of the subsequent redundant channel coding and the inserted signaling bits, the gross data rate – i.e., the transmission rate of the transmitted signal $s(t)$ – is greater.
A measure for the quality of the entire ISDN transmission system is the sink SNR
- $$\rho_{v} = \frac{P_q}{P_{\varepsilon}} = \frac{\overline{q(t)^2}}{\overline{[\upsilon(t) - q(t)]^2}}$$
as the ratio of the powers
- of the analog signal $q(t)$ bandlimited to the range $300 \ {\rm Hz}\ \text{...}\ 3400 \ {\rm Hz}$
- and the error signal $\varepsilon (t) = v (t) - q(t)$.
An ideal signal reconstruction with an ideal rectangular low-pass filter is assumed here for the sink signal $v (t)$.
Notes:
- The exercise refers to the chapter "General Description of ISDN" of this book.
- Reference is also made to the chapter "Pulse Code Modulation" of the book "Modulation Methods".
Questions
Solution
(1) The quantization level number $M$ is usually chosen as a power of two and for the number of bits $N = {\log_2}\hspace{0.05cm}(M)$.
- From $M = 2^{8} = 256$ follows $\underline{N = 8}$.
(2) For the bit rate, $R_{\rm B} = N \cdot f_{\rm A}$.
- Thus, from $R_{\rm B} = 64 \ \rm kbit/s$ and $N = 8$, we get $f_{\rm A} \hspace{0.15cm}\underline{= 8 \ \rm kHz}$.
(3) Due to the bandwidth limitation, the highest frequency contained in the signal $q(t)$ is equal to $3.4 \ \rm kHz$.
- Therefore, according to the sampling theorem, $f_{\rm A} ≥ 6.8 \ \rm kHz$ should hold.
- With $f_{\rm A} = 8 \ \rm kHz$ the condition is fulfilled ⇒ $\underline {\rm YES}$.
(4) The last statement is correct:
- Even if the influence of the AWGN noise is small $($small noise power density $N_{0})$, the sink SNR $\rho_{v}$ cannot fall below a limit given by the quantization noise:
- $$\rho_{v} \approx \rho_{\rm Q} = 2^{2M} = 2^{16} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} \approx 48\, {\rm dB}\hspace{0.05cm}.$$
- With larger noise interference, $\rho_{v}$ can further (significantly) be reduced by the transmission errors.
- In contrast, sampling results in no loss of quality if the sampling theorem is obeyed.
- Sampling can then be completely undone if the source signal $q(t)$ is bandlimited and the signal reconstruction is correctly dimensioned ⇒ ideal low-pass.