Difference between revisions of "Aufgaben:Exercise 1.16Z: Bounds for the Gaussian Error Function"
m (Text replacement - "[[Stochastische_Signaltheorie/" to "[[Theory_of_Stochastic_Signals/") |
|||
| (15 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Limits_for_Block_Error_Probability}} |
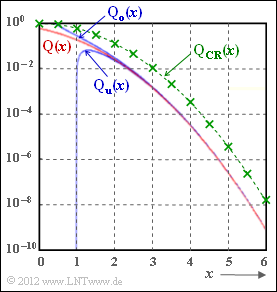
| − | [[File:P_ID2415__KC_A_1_15.png|right|frame|${\rm Q}(x)$ | + | [[File:P_ID2415__KC_A_1_15.png|right|frame|Function ${\rm Q}(x)$ and approximations;<br>it holds: ${\rm Q_u}(x)\le{\rm Q}(x)\le{\rm Q_o}(x)$]] |
| − | + | The probability that a zero-mean Gaussian random variable $n$ with standard deviation $\sigma$ ⇒ variance $\sigma^2$ is greater in magnitude than a given value $A$ is equal to | |
:$${\rm Pr}(n > A) = {\rm Pr}(n < -A) ={\rm Q}(A/\sigma) \hspace{0.05cm}.$$ | :$${\rm Pr}(n > A) = {\rm Pr}(n < -A) ={\rm Q}(A/\sigma) \hspace{0.05cm}.$$ | ||
| − | + | Here is used one of the most important functions for Communications Engineering (drawn in red in the diagram): <br>the [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables#Exceedance_probability|"complementary Gaussian error function"]] | |
:$${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$ | :$${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$ | ||
| − | ${\rm Q}(x)$ | + | ${\rm Q}(x)$ is a monotonically decreasing function with ${\rm Q}(0) = 0.5$. For very large values of $x$ ⇒ ${\rm Q}(x)$ tends $\to 0$. |
| − | + | The integral of the ${\rm Q}$–function is not analytically solvable and is usually given in tabular form. From the literature, however, manageable approximations or bounds for positive $x$ values are known: | |
| − | * | + | *the "upper bound" ⇒ upper $($German: "obere" ⇒ subscript: "o"$)$ blue curve in adjacent graph, valid for $x > 0$: |
:$$ {\rm Q_o}(x)=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2}\hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$ | :$$ {\rm Q_o}(x)=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2}\hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$ | ||
| − | * | + | *the "lower bound" ⇒ upper $($German: "untere" ⇒ subscript: "u"$)$ blue curve in adjacent graph, valid for $x > 1$: |
| − | |||
:$$ {\rm Q_u}(x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \le \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$ | :$$ {\rm Q_u}(x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \le \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$ | ||
| − | * | + | *the "Chernoff-Rubin bound" $($green curve in the graph, drawn for $K = 1)$: |
:$${\rm Q_{CR}}(x)=K \cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm}.$$ | :$${\rm Q_{CR}}(x)=K \cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm}.$$ | ||
| − | In | + | In the exercise it is to be investigated to what extent these bounds can be used as approximations for ${\rm Q}(x)$ and what corruptions result. |
| − | |||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Bounds_for_Block_Error_Probability|"Bounds for block error probability"]]. | ||
| + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Gaussian_Distributed_Random_Variables|"Gaussian distributed random variables"]] in the book "Stochastic Signal Theory". | ||
| + | |||
| + | *The exercise provides some important hints for solving [[Aufgaben:Exercise_1.16:_Block_Error_Probability_Bounds_for_AWGN|"Exercise 1.16"]], in which ${\rm Q}_{\rm CR}(x)$ is used to derive the [[Channel_Coding/Limits_for_Block_Error_Probability#The_upper_bound_according_to_Bhattacharyya|"Bhattacharyya Bound"]] for the AWGN channel. | ||
| + | |||
| + | * Further we refer to the interactive HTML5/JavaScript applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen| "Complementary Gaussian error functions"]]. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 46: | Line 46: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What values do the upper and lower bounds for $x = 4$ provide? |
|type="{}"} | |type="{}"} | ||
${\rm Q_{o}}(x = 4) \ = \ $ { 3.346 3% }$\ \cdot 10^{-5} $ | ${\rm Q_{o}}(x = 4) \ = \ $ { 3.346 3% }$\ \cdot 10^{-5} $ | ||
${\rm Q_{u}}(x = 4) \ = \ $ { 3.137 3% }$\ \cdot 10^{-5} $ | ${\rm Q_{u}}(x = 4) \ = \ $ { 3.137 3% }$\ \cdot 10^{-5} $ | ||
| − | { | + | {What statements hold for the functions ${\rm Q_{o}}(x)$ and ${\rm Q_{u}}(x)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + For $x ≥ 2$: Both bounds are usable. |
| − | + | + | + For $x < 1$: ${\rm Q_{u}}(x)$ is unusable $($because ${\rm Q_{u}}(x)< 0)$. |
| − | - | + | - For $x < 1$: ${\rm Q_{o}}(x)$ is unusable $($because ${\rm Q_{o}}(x)> 1)$. |
| − | { | + | {By what factor is the Chernoff-Rubin Bound above ${\rm Q_{o}}(x)$? |
|type="{}"} | |type="{}"} | ||
${\rm Q}_{\rm CR}(x = 2)/{\rm Q_{o}}(x = 2 ) \ = \ $ { 5 3% } | ${\rm Q}_{\rm CR}(x = 2)/{\rm Q_{o}}(x = 2 ) \ = \ $ { 5 3% } | ||
| Line 68: | Line 68: | ||
${\rm Q}_{\rm CR}(x = 6)/{\rm Q_{o}}(x = 6 ) \ = \ $ { 15 3% } | ${\rm Q}_{\rm CR}(x = 6)/{\rm Q_{o}}(x = 6 ) \ = \ $ { 15 3% } | ||
| − | { | + | {Determine $K$ such that $K \cdot {\rm Q}_{\rm CR}(x)$ is as close as possible to ${\rm Q}(x)$ and at the same time ${\rm Q}(x) ≤ K · {\rm Q}_{\rm CR}(x)$ is observed for all $x > 0$ . |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 0.5 3% } | $K \ = \ $ { 0.5 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The upper bound is: |
:$${\rm Q_o}(x)=\frac{1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_o}(4 )=\frac{1}{\sqrt{\rm 2\pi}\cdot 4}\cdot {\rm e}^{-8 }\hspace{0.15cm}\underline{\approx 3.346 \cdot 10^{-5}}\hspace{0.05cm}.$$ | :$${\rm Q_o}(x)=\frac{1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_o}(4 )=\frac{1}{\sqrt{\rm 2\pi}\cdot 4}\cdot {\rm e}^{-8 }\hspace{0.15cm}\underline{\approx 3.346 \cdot 10^{-5}}\hspace{0.05cm}.$$ | ||
| − | * | + | *The lower bound can be converted as follows: |
:$${\rm Q_u}( x)=(1-1/x^2) \cdot {\rm Q_o}(x) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_u}(4 ) \hspace{0.15cm}\underline{\approx 3.137 \cdot 10^{-5}} \hspace{0.05cm}.$$ | :$${\rm Q_u}( x)=(1-1/x^2) \cdot {\rm Q_o}(x) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_u}(4 ) \hspace{0.15cm}\underline{\approx 3.137 \cdot 10^{-5}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The relative deviations from the actual value ${\rm Q}(4) = 3.167 · 10^{–5}$ are $+5\%$ resp. $–1\%$. |
| + | |||
| + | '''(2)''' Correct are the <u>solutions 1 and 2</u>: | ||
| + | *For $x = 2$, the actual function value ${\rm Q}(x) = 2.275 \cdot 10^{-2}$ is bounded by ${\rm Q_{o}}(x) = 2.7 \cdot 10^{-2}$ and ${\rm Q_u}(x) = 2.025 \cdot 10^{-2}$, respectively. | ||
| + | |||
| + | *The relative deviations are therefore $18.7\%$ resp. $-11\%,$. | ||
| − | + | *The last statement is wrong: Only for $x < 0.37$ ⇒ ${\rm Q_o}(x) > 1$ is valid. | |
| − | |||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(3)''' For the quotient of ${\rm Q}_{\rm CR}(x)$ and ${\rm Q_o}(x)$, according to the given equations: |
:$$q(x) = \frac{{\rm Q_{CR}}(x)}{{\rm Q_{o}}(x)} = \frac{{\rm exp}(-x^2/2)}{{\rm exp}(-x^2/2)/({\sqrt{2\pi} \cdot x})} = {\sqrt{2\pi} \cdot x}$$ | :$$q(x) = \frac{{\rm Q_{CR}}(x)}{{\rm Q_{o}}(x)} = \frac{{\rm exp}(-x^2/2)}{{\rm exp}(-x^2/2)/({\sqrt{2\pi} \cdot x})} = {\sqrt{2\pi} \cdot x}$$ | ||
| Line 101: | Line 103: | ||
:$$\Rightarrow \hspace{0.3cm} q(x) \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} q(x =2) \hspace{0.15cm}\underline{=5}\hspace{0.05cm}, \hspace{0.2cm}q(x =4)\hspace{0.15cm}\underline{=10}\hspace{0.05cm}, \hspace{0.2cm}q(x =6) \hspace{0.15cm}\underline{=15}\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} q(x) \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} q(x =2) \hspace{0.15cm}\underline{=5}\hspace{0.05cm}, \hspace{0.2cm}q(x =4)\hspace{0.15cm}\underline{=10}\hspace{0.05cm}, \hspace{0.2cm}q(x =6) \hspace{0.15cm}\underline{=15}\hspace{0.05cm}.$$ | ||
| − | * | + | *The larger the abscissa value $x$ is, the more inaccurately ${\rm Q}(x)$ is approximated by ${\rm Q}_{\rm CR}(x)$. |
| − | * | + | |
| + | *When looking at the graph in the information section, I first had the impression that ${\rm Q}_{\rm CR}(x)$ results from ${\rm Q}(x)$ by shifting to the right or shifting up. | ||
| + | |||
| + | *But this is only an optical illusion and does not correspond to the facts. | ||
| − | '''(4)''' | + | '''(4)''' With $\underline{K = 0.5}$ the new bound $0.5 \cdot {\rm Q}_{\rm CR}(x)$ for $x = 0$ agrees exactly with ${\rm Q}(x=0) = 0.500$. |
| − | * | + | *For larger abscissa values, the falsification $q \approx 1.25 \cdot x$ thus also becomes only half as large. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^1.6 Error Probability Bounds^]] |
Latest revision as of 17:03, 23 January 2023
The probability that a zero-mean Gaussian random variable $n$ with standard deviation $\sigma$ ⇒ variance $\sigma^2$ is greater in magnitude than a given value $A$ is equal to
- $${\rm Pr}(n > A) = {\rm Pr}(n < -A) ={\rm Q}(A/\sigma) \hspace{0.05cm}.$$
Here is used one of the most important functions for Communications Engineering (drawn in red in the diagram):
the "complementary Gaussian error function"
- $${\rm Q} (x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm}.$$
${\rm Q}(x)$ is a monotonically decreasing function with ${\rm Q}(0) = 0.5$. For very large values of $x$ ⇒ ${\rm Q}(x)$ tends $\to 0$.
The integral of the ${\rm Q}$–function is not analytically solvable and is usually given in tabular form. From the literature, however, manageable approximations or bounds for positive $x$ values are known:
- the "upper bound" ⇒ upper $($German: "obere" ⇒ subscript: "o"$)$ blue curve in adjacent graph, valid for $x > 0$:
- $$ {\rm Q_o}(x)=\frac{\rm 1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2}\hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$
- the "lower bound" ⇒ upper $($German: "untere" ⇒ subscript: "u"$)$ blue curve in adjacent graph, valid for $x > 1$:
- $$ {\rm Q_u}(x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot x}\cdot \rm e^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \le \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm},$$
- the "Chernoff-Rubin bound" $($green curve in the graph, drawn for $K = 1)$:
- $${\rm Q_{CR}}(x)=K \cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.15cm} \ge \hspace{0.15cm} {\rm Q} (x) \hspace{0.05cm}.$$
In the exercise it is to be investigated to what extent these bounds can be used as approximations for ${\rm Q}(x)$ and what corruptions result.
Hints:
- This exercise belongs to the chapter "Bounds for block error probability".
- Reference is also made to the chapter "Gaussian distributed random variables" in the book "Stochastic Signal Theory".
- The exercise provides some important hints for solving "Exercise 1.16", in which ${\rm Q}_{\rm CR}(x)$ is used to derive the "Bhattacharyya Bound" for the AWGN channel.
- Further we refer to the interactive HTML5/JavaScript applet "Complementary Gaussian error functions".
Questions
Solution
- $${\rm Q_o}(x)=\frac{1}{\sqrt{\rm 2\pi}\cdot x}\cdot {\rm e}^{-x^{\rm 2}/\rm 2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_o}(4 )=\frac{1}{\sqrt{\rm 2\pi}\cdot 4}\cdot {\rm e}^{-8 }\hspace{0.15cm}\underline{\approx 3.346 \cdot 10^{-5}}\hspace{0.05cm}.$$
- The lower bound can be converted as follows:
- $${\rm Q_u}( x)=(1-1/x^2) \cdot {\rm Q_o}(x) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q_u}(4 ) \hspace{0.15cm}\underline{\approx 3.137 \cdot 10^{-5}} \hspace{0.05cm}.$$
- The relative deviations from the actual value ${\rm Q}(4) = 3.167 · 10^{–5}$ are $+5\%$ resp. $–1\%$.
(2) Correct are the solutions 1 and 2:
- For $x = 2$, the actual function value ${\rm Q}(x) = 2.275 \cdot 10^{-2}$ is bounded by ${\rm Q_{o}}(x) = 2.7 \cdot 10^{-2}$ and ${\rm Q_u}(x) = 2.025 \cdot 10^{-2}$, respectively.
- The relative deviations are therefore $18.7\%$ resp. $-11\%,$.
- The last statement is wrong: Only for $x < 0.37$ ⇒ ${\rm Q_o}(x) > 1$ is valid.
(3) For the quotient of ${\rm Q}_{\rm CR}(x)$ and ${\rm Q_o}(x)$, according to the given equations:
- $$q(x) = \frac{{\rm Q_{CR}}(x)}{{\rm Q_{o}}(x)} = \frac{{\rm exp}(-x^2/2)}{{\rm exp}(-x^2/2)/({\sqrt{2\pi} \cdot x})} = {\sqrt{2\pi} \cdot x}$$
- $$\Rightarrow \hspace{0.3cm} q(x) \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} q(x =2) \hspace{0.15cm}\underline{=5}\hspace{0.05cm}, \hspace{0.2cm}q(x =4)\hspace{0.15cm}\underline{=10}\hspace{0.05cm}, \hspace{0.2cm}q(x =6) \hspace{0.15cm}\underline{=15}\hspace{0.05cm}.$$
- The larger the abscissa value $x$ is, the more inaccurately ${\rm Q}(x)$ is approximated by ${\rm Q}_{\rm CR}(x)$.
- When looking at the graph in the information section, I first had the impression that ${\rm Q}_{\rm CR}(x)$ results from ${\rm Q}(x)$ by shifting to the right or shifting up.
- But this is only an optical illusion and does not correspond to the facts.
(4) With $\underline{K = 0.5}$ the new bound $0.5 \cdot {\rm Q}_{\rm CR}(x)$ for $x = 0$ agrees exactly with ${\rm Q}(x=0) = 0.500$.
- For larger abscissa values, the falsification $q \approx 1.25 \cdot x$ thus also becomes only half as large.