Aufgaben:Exercise 4.5: Pseudo Noise Modulation

• Return to book

Ersatzschaltbild von PN-Modulation und BPSK

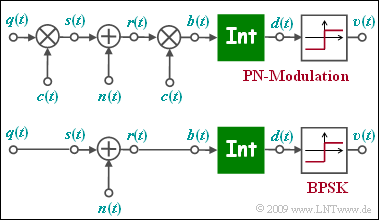
Die Grafik zeigt oben das Ersatzschaltbild der "Pseudo Noise"–Modulation  (englisch:  Direct Sequence Spread Spectrum, abgekürzt  DS–SS)  im äquivalenten Tiefpass–Bereich. $n(t)$  bezeichnet AWGN–Rauschen.

Unten ist das Tiefpass–Modell der  binären Phasenmodulation  (englisch:  Binary Phase Shift Keying,  BPSK) skizziert.

• Das Tiefpass–Sendesignal  $s(t)$  ist nur aus Gründen einheitlicher Darstellung gleich dem rechteckförmigen Quellensignal  $q(t) ∈ \{+1, –1\}$  mit Rechteckdauer  $T$  gesetzt ist.
• Die Funktion des Integrators kann wie folgt geschrieben werden:

$$d (\nu T) = \frac{1}{T} \cdot \hspace{0.03cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t \hspace{0.05cm}.$$

• Die beiden Modelle unterscheiden sich durch die Multiplikation mit dem  $±1$–Spreizsignal  $c(t)$  bei Sender und Empfänger, wobei von  $c(t)$  lediglich der Spreizgrad  $J$  bekannt ist.
• Für die Lösung dieser Aufgabe ist die Angabe der spezifischen Spreizfolge  (M–Sequenz oder Walsh–Funktion)  nicht von Bedeutung.

Zu untersuchen ist, ob sich das untere BPSK–Modell auch bei PN–Modulation anwenden lässt und ob die BPSK–Fehlerwahrscheinlichkeit

$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$

auch für die PN–Modulation gültig ist, bzw. wie die angegebene Gleichung zu modifizieren ist.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Nachrichtentechnische Aspekte von UMTS.
• Das bei UMTS eingesetzte CDMA–Verfahren firmiert auch unter der Bezeichnung „PN–Modulation”.
• Die in dieser Aufgabe verwendete Nomenklatur richtet sich zum Teil nach dem Kapitel  PN–Modulation  im Buch „Modulationsverfahren”.

Fragebogen

1

Welche Detektionssignalwerte sind bei BPSK im rauschfreien Fall möglich?

	$d(\nu T)$  ist gaußverteilt.
	$d(\nu T)$  kann die Werte  $+1, \ 0$  und  $–1$  annehmen.
	Es sind nur die Werte  $d(\nu T) = +1$  und  $d(\nu T) = -1$  möglich.

2

Welche Werte sind bei PN–Modulation im rauschfreien Fall möglich?

	$d(\nu T)$  ist gaußverteilt.
	$d(\nu T)$  kann die Werte  $+1, \ 0$  und  $–1$  annehmen.
	Es sind nur die Werte  $d(\nu T) = +1$  und  $d(\nu T) = -1$  möglich.

3

Welche Modifikation muss am BPSK–Modell vorgenommen werden, damit es auch für die PN–Modulation anwendbar ist?

	Das Rauschen  $n(t)$  muss durch  $n\hspace{0.05cm}'(t) = n(t) \cdot c(t)$  ersetzt werden.
	Die Integration muss nun über  $J \cdot T$  erfolgen.
	Die Rauschleistung muss um den Faktor  $J$  vermindert werden.

4

Welche Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  ergibt sich für  $10 \cdot {\rm lg} \ (E_{\rm B}/N_{0}) = 6 \ \rm dB$  bei PN–Modulation?
Hinweis:   Bei BPSK gilt in diesem Fall:   $p_{\rm B} \approx 2.3 \cdot 10^{–3}$.

	Je größer  $J$  gewählt wird, desto kleiner ist  $p_{\rm B}$.
	Je größer  $J$  gewählt wird, desto größer ist  $p_{\rm B}$.
	Es ergibt sich unabhängig von  $J$  stets der Wert  $2.3 \cdot 10^{–3}$.

Musterlösung

Solution

(1)  Richtig ist der letzte Lösungsvorschlag:

• Es handelt sich hier um einen optimalen Empfänger.
• Ohne Rauschen ist Signal  $b(t)$  innerhalb eines jeden Bits konstant gleich $+1$ oder $-1$.
• Aus der angegebenen Gleichung für den Integrator folgt, dass  $d(\nu T)$  nur die Werte $±1$ annehmen kann:

$$d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T} \hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t.$$

(2)  Richtig ist wieder der letzte Lösungsvorschlag:

• Im rauschfreien Fall   ⇒   $n(t) = 0$ kann auf die zweifache Multiplikation mit  $c(t) ∈ \{+1, –1\} \ \Rightarrow \ c(t)^{2} = 1$  verzichtet werden,
• so dass das obere Modell mit dem unteren Modell identisch ist.

(3)  Zutreffend ist nur der Lösungsvorschlag 1:

• Da beide Modelle im rauschfreien Fall identisch sind, muss nur das Rauschsignal angepasst werden:   $n\hspace{0.05cm}'(t) = n(t) \cdot c(t)$.
• Die Vorschläge 2 und 3 sind dagegen nicht zutreffend:   Die Integration muss weiterhin über  $T = J \cdot T_{\rm c}$  erfolgen und die PN–Modulation verringert das AWGN–Rauschen nicht.

(4)  Richtig ist der letzte Lösungsvorschlag.:

• Multipliziert man das AWGN–Rauschen mit dem hochfrequenten  $±1$–Signal  $c(t)$, so ist das Rauschen ebenfalls gaußförmig und weiß.
• Wegen  $E[c^{2}(t)] = 1$  wird auch die Rauschvarianz nicht verändert. Die für BPSK gültige Gleichung

$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B}}/{N_{\rm 0}} } \hspace{0.05cm} \right )$$

ist somit auch bei der PN–Modulation anwendbar und zwar unabhängig vom Spreizfaktor  $J$  und von der spezifischen Spreizfolge.

  ⇒   Bei AWGN–Rauschen wird also die Fehlerwahrscheinlichkeit durch Bandspreizung weder vergrößert noch verkleinert.