Difference between revisions of "Applets:Generation of Walsh functions"
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLinkEnDe|walsh_en|walsh}} |
== Program description== | == Program description== | ||
<br> | <br> | ||
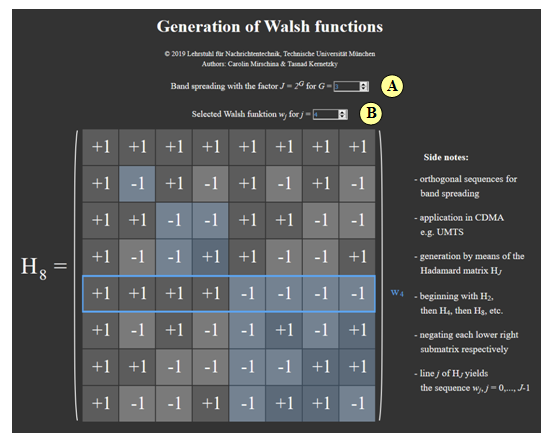
| − | This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by blue | + | This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by means of a blue border around rows of the matrix) can be changed. |
==Theoretical background== | ==Theoretical background== | ||
| Line 9: | Line 9: | ||
===Application=== | ===Application=== | ||
<br> | <br> | ||
| − | The '''Walsh functions''' are a group of periodic orthogonal functions. Their application in digital signal processing | + | The '''Walsh functions''' are a group of periodic orthogonal functions. Their application in digital signal processing mainly lies in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS. |
*Due to their orthogonal properties and the favourable periodic cross-correlation function $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system. If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero. | *Due to their orthogonal properties and the favourable periodic cross-correlation function $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system. If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero. | ||
*In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading. | *In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading. | ||
| − | *In terms of $\rm (PACF)$ (''periodic | + | *In terms of $\rm (PACF)$ (''periodic autocorrelation function'') these sequences are not as good: Each individual Walsh function has a different PACF and each individual PACF is less good than a comparable pseudo noise $\rm (PN)$ sequence. That means: The synchronization is more difficult with Walsh functions than with PN sequences. |
<br> | <br> | ||
| Line 39: | Line 39: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
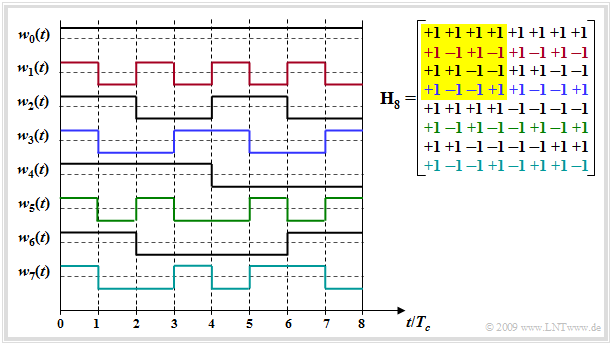
| − | $\text{Example:}$ The graphic shows the Hadamard matrix $\mathbf H_8$ (right) and the $J -1$ spreading sequences which can be constructed with it. | + | $\text{Example:}$ The graphic shows the Hadamard matrix $\mathbf H_8$ (right) and the $J\hspace{-0.09cm} -\hspace{-0.09cm}1$ spreading sequences which can be constructed with it. |
[[File:P_ID1882__Mod_T_5_3_S7_neu.png|right|frame| Walsh spreading sequences $(J = 8)$ and Hadamard matrix $\mathbf H_8$ ]] | [[File:P_ID1882__Mod_T_5_3_S7_neu.png|right|frame| Walsh spreading sequences $(J = 8)$ and Hadamard matrix $\mathbf H_8$ ]] | ||
| − | *$J - 1$ because the | + | *Only $J\hspace{-0.09cm} -\hspace{-0.09cm}1$, because the unspreaded sequence $w_0(t)$ is usually not used. |
*Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$. | *Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$. | ||
| − | *The | + | *The submatrix $\mathbf H_4$ is highlighted in yellow.}} |
<br clear=all> | <br clear=all> | ||
| Line 49: | Line 49: | ||
<br> | <br> | ||
| − | [[File: | + | [[File:Bildschirm_Walsh_EN_3.png|right|600px]] |
| − | '''(A)''' Selection of | + | '''(A)''' Selection of $G$ ⇒ Band spread factor: $J= 2^G$ |
| − | '''(B)''' Selection of the | + | '''(B)''' Selection of the Walsh function $w_j$ to be marked |
<br clear=all> | <br clear=all> | ||
== About the authors== | == About the authors== | ||
| − | + | This interactive calculation tool was designed and realized at the [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] $\rm (LNT)$ of the [https://www.tum.de/ Technical University of Munich] $\rm (TUM)$. | |
| − | |||
| − | |||
| − | == | + | *The first German version was created in 2007 by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Thomas_Gro.C3.9Fer_.28Diplomarbeit_LB_2006.2C_danach_freie_Mitarbeit_bis_2010.29|Thomas Großer]] in the context of his diploma thesis with "FlashMX–Actionscript" (Supervisor: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| + | *2018/2019 the applet was converted on "HTML5" and redesigned by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] (Engineering practice, supervisor: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]] ). | ||
| + | *2020 this English version was made by [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] (working student) and [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]. | ||
| + | ==Call the applet again== | ||
<br> | <br> | ||
| − | {{ | + | {{LntAppletLinkEnDe|walsh_en|walsh}} |
| − | + | <br><br> | |
Latest revision as of 19:05, 21 March 2023
Open Applet in new Tab Deutsche Version Öffnen
Contents
Program description
This applet allows to display the Hadamard matrices $\mathbf{H}_J$ for the construction of the Walsh functions $w_j$. The factor $J$ of the band spreading as well as the selection of the individual Walsh functions (by means of a blue border around rows of the matrix) can be changed.
Theoretical background
Application
The Walsh functions are a group of periodic orthogonal functions. Their application in digital signal processing mainly lies in the use for band spreading in CDMA systems, for example the mobile radio standard UMTS.
- Due to their orthogonal properties and the favourable periodic cross-correlation function $\rm (PCCF)$, the Walsh functions represent optimal spreading sequences for a distortion-free channel and a synchronous CDMA system. If you take any two lines and form the correlation (averaging over the products), the PCCF value is always zero.
- In asynchronous operation (example: uplink of a mobile radio system) or de-orthogonalization due to multipath propagation, Walsh functions alone are not necessarily suitable for band spreading.
- In terms of $\rm (PACF)$ (periodic autocorrelation function) these sequences are not as good: Each individual Walsh function has a different PACF and each individual PACF is less good than a comparable pseudo noise $\rm (PN)$ sequence. That means: The synchronization is more difficult with Walsh functions than with PN sequences.
Construction
The construction of Walsh functions can be done recursively using the Hadamard matrices.
- A Hadamard matrix $\mathbf{H}_J$ of order $J$ is a $J\times J$ matrix, which contains line by line the $\pm 1$ weights of the Walsh sequences.
- The orders of the Hadamard matrices are fixed to powers of two, i.e. $J = 2^G$ applies to a natural number $G$. Starting from $\mathbf{H}_1 = [+1]$ and
- $$ \mathbf{H}_2 = \left[ \begin{array}{rr} +1 & +1\\ +1 & -1 \\ \end{array}\right] $$
the following relationship applies to the generation of further Hadamard matrices:
- $$ \mathbf{H}_{2N} = \left[ \begin{array}{rr} +\mathbf{H}_N & +\mathbf{H}_N\\ +\mathbf{H}_N & -\mathbf{H}_N \\ \end{array}\right] $$
$\text{Example:}$ The graphic shows the Hadamard matrix $\mathbf H_8$ (right) and the $J\hspace{-0.09cm} -\hspace{-0.09cm}1$ spreading sequences which can be constructed with it.
- Only $J\hspace{-0.09cm} -\hspace{-0.09cm}1$, because the unspreaded sequence $w_0(t)$ is usually not used.
- Please note the color assignment between the lines of the Hadamard matrix and the spreading sequences $w_j(t)$.
- The submatrix $\mathbf H_4$ is highlighted in yellow.
How to use the applet
(A) Selection of $G$ ⇒ Band spread factor: $J= 2^G$
(B) Selection of the Walsh function $w_j$ to be marked
About the authors
This interactive calculation tool was designed and realized at the Lehrstuhl für Nachrichtentechnik $\rm (LNT)$ of the Technical University of Munich $\rm (TUM)$.
- The first German version was created in 2007 by Thomas Großer in the context of his diploma thesis with "FlashMX–Actionscript" (Supervisor: Günter Söder).
- 2018/2019 the applet was converted on "HTML5" and redesigned by Carolin Mirschina (Engineering practice, supervisor: Tasnád Kernetzky ).
- 2020 this English version was made by Carolin Mirschina (working student) and Günter Söder.