Difference between revisions of "Applets:Sampling of Analog Signals and Signal Reconstruction"
| Line 52: | Line 52: | ||
===Description of sampling in the time domain=== | ===Description of sampling in the time domain=== | ||
| − | [[File:P_ID1120__Sig_T_5_1_S1_neu.png|center|frame| | + | [[File:P_ID1120__Sig_T_5_1_S1_neu.png|center|frame|For the time discretization of the continuous-time signal $x(t)$]] |
| − | + | In the following, we use the following nomenclature to describe the sampling: | |
| − | * | + | *let the continuous-time signal be $x(t)$. |
| − | * | + | *Let the time-discretized signal sampled at equidistant intervals $T_{\rm A}$ be $x_{\rm A}(t)$. |
| − | * | + | *Out of the sampling time points $\nu \cdot T_{\rm A}$ always holds $x_{\rm A}(t) \equiv 0$. |
| − | * | + | *The run variable $\nu$ be an [[Signal_Representation/Calculating_with_Complex_Numbers#The_set_of_real_numbers|"integer"]]: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $. |
| − | * | + | *In contrast, at the equidistant sampling times with the constant $K$, the result is: |
:$$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$ | :$$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$ | ||
| − | + | The constant depends on the type of time discretization. For the above sketch $K = 1$ is valid. | |
<br><br> | <br><br> | ||
| − | ===Description of sampling with Dirac pulse | + | ===Description of sampling with the Dirac delta pulse=== |
| − | + | In the following, we assume a slightly different form of description. The following pages will show that these equations, which take some getting used to, do lead to useful results if they are applied consistently. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Definitions:}$ |
| − | * | + | * By '''sampling''' we mean here the multiplication of the time-continuous signal $x(t)$ by a '''Dirac delta pulse''': |
:$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$ | :$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$ | ||
| − | * | + | *The '''Dirac delta pulse (in the time domain)''' consists of infinitely many Dirac delta pulses, each equally spaced $T_{\rm A}$ and all with equal momentum weight $T_{\rm A}$: |
:$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot | :$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot | ||
| Line 83: | Line 83: | ||
| − | + | Based on this definition, the following properties result for the sampled signal: | |
:$$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot | :$$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot | ||
\delta (t- \nu \cdot T_{\rm A} | \delta (t- \nu \cdot T_{\rm A} | ||
)\hspace{0.05cm}.$$ | )\hspace{0.05cm}.$$ | ||
| − | * | + | *The sampled signal at the considered time $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$. |
| − | * | + | *Since $\delta (t)$ at time $t = 0$ is infinite, actually all signal values $x_{\rm A}(\nu \cdot T_{\rm A})$ are also infinite and also the factor $K$ introduced above. |
| − | * | + | *Two samples $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ and $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ however, differ in the same proportion as the signal values $x(\nu_1 \cdot T_{\rm A})$ and $x(\nu_2 \cdot T_{\rm A})$. |
| − | * | + | *The samples of $x(t)$ appear in the momentum weights of the Dirac functions: |
| − | * | + | *The additional multiplication by $T_{\rm A}$ is necessary so that $x(t)$ and $x_{\rm A}(t)$ have the same unit. Note here that $\delta (t)$ itself has the unit "1/s". |
===Description of sampling in the frequency domain=== | ===Description of sampling in the frequency domain=== | ||
| − | Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des [[Signal_Representation/The_Convolution_Theorem_and_Operation# | + | Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_in_the_frequency_domain|"Faltungssatzes"]]. Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht: |
:$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | :$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | ||
X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$ | X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$ | ||
| − | Entwickelt man den Diracpuls $p_{\delta}(t)$ (im Zeitbereich) in eine [[Signal_Representation/ | + | Entwickelt man den Diracpuls $p_{\delta}(t)$ (im Zeitbereich) in eine [[Signal_Representation/Fourier_Series|"Fourierreihe"]] und transformiert diese unter Anwendung des [[Signal_Representation/The_Fourier_Transform_Theorems#Shifting_Theorem|"Verschiebungssatzes"]] in den Frequenzbereich, so ergibt sich mit dem Abstand $f_{\rm A} = 1/T_{\rm A}$ zweier benachbarter Diraclinien im Frequenzbereich folgende Korrespondenz ⇒ [[Signal_Representation/Discrete-Time_Signal_Representation#Dirac_comb_in_time_and_frequency_domain|"Beweis"]]: |
:$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot | :$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot | ||
| Line 114: | Line 114: | ||
*Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$. | *Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$. | ||
*Auch $P_{\delta}(f)$ besteht aus unendlich vielen Diracimpulsen, nun im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$. | *Auch $P_{\delta}(f)$ besteht aus unendlich vielen Diracimpulsen, nun im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$. | ||
| − | *Die Abstände der Diraclinien in Zeit– und Frequenzbereich folgen demnach dem [[Signal_Representation/ | + | *Die Abstände der Diraclinien in Zeit– und Frequenzbereich folgen demnach dem [[Signal_Representation/The_Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|"Reziprozitätsgesetz"]]: $T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$ |
| Line 156: | Line 156: | ||
<br>Die Lösung ist einfach, wenn man die Spektralfunktionen betrachtet: | <br>Die Lösung ist einfach, wenn man die Spektralfunktionen betrachtet: | ||
| − | Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch ein Tiefpass Filter mit dem [[Linear_and_Time_Invariant_Systems/ | + | Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch ein Tiefpass Filter mit dem [[Linear_and_Time_Invariant_Systems/System_Description_in_Frequency_Domain#Frequency_response_.E2.80.93_Transfer_function|"Frequenzgang"]] $H_{\rm E}(f)$, der |
*die tiefen Frequenzen unverfälscht durchlässt: | *die tiefen Frequenzen unverfälscht durchlässt: | ||
Revision as of 18:58, 25 March 2023
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
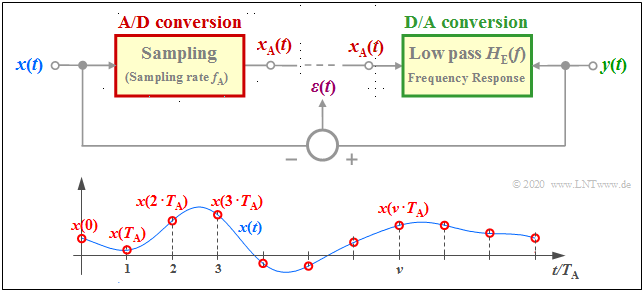
The applet deals with the system components "sampling" and "signal reconstruction", two components that are of great importance for understanding the Pulscodemodulation $({\rm PCM})$ for example. The upper graphic shows the model on which this applet is based. Below it are the samples $x(\nu \cdot T_{\rm A})$ of the time continuous signal $x(t)$. The (infinite) sum over all these samples is called the sampled signal $x_{\rm A}(t)$.
- At the transmitter, the time discrete (sampled) signal $x_{\rm A}(t)$ is obtained from the continuous–time signal $x(t)$. This process is called sampling or A/D conversion.
- The corresponding program parameter for the transmitter is the sampling rate $f_{\rm A}= 1/T_{\rm A}$. The lower graphic shows the sampling distance $T_{\rm A}$ .
- In the receiver, the discrete-time received signal $y_{\rm A}(t)$ is used to generate the continuous-time sink signal $y(t)$ ⇒ signal reconstruction or D/A conversion corresponding to the receiver frequency response $H_{\rm E}(f)$.
The applet does not consider the PCM blocks "Quantization"and "encoding/decoding". The digital transmission channel is assumed to be ideal.
The following consequences result from this:
- In the program simplifying $y_{\rm A}(t) = x_{\rm A}(t)$ is set.
- With suitable system parameters, the error signal $\varepsilon(t) = y(t)-x(t)\equiv 0$ is therefore also possible.
The sampling theorem and the signal reconstruction can be better explained in the frequency domain. Therefore all spectral functions are displayed in the program;
$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t)$, $X_{\rm A}(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x_{\rm A}(t)$, $Y(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ y(t)$, $E(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ \varepsilon(t).$
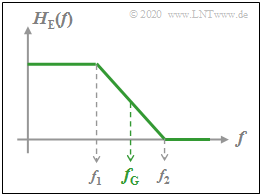
Parameters for the receiver frequency response $H_{\rm E}(f)$ are the cut–off frequency and the rolloff factor (see lower graph):
- $$f_{\rm G} = \frac{f_2 +f_1}{2},\hspace{1cm}r = \frac{f_2 -f_1}{f_2 +f_1}.$$
Notes:
(1) All signal values are normalized to $\pm 1$.
(2) The power calculation is done by integration over the respective period duration $T_0$:
- $$P_x = \frac{1}{T_0} \cdot \int_0^{T_0} x^2(t)\ {\rm d}t,\hspace{0.8cm}P_\varepsilon = \frac{1}{T_0} \cdot \int_0^{T_0} \varepsilon^2(t).$$
(3) The signal power $P_x$ and the distortion power $P_\varepsilon$ are also output in normalized form, which implicitly assumes the reference resistance $R = 1\, \rm \Omega$ ;
(4) From these the signal–distortion–distance $10 \cdot \lg \ (P_x/P_\varepsilon)$ can be calculated.
(5) Does the spectral function $X(f)$ for positive frequencies consists of $I$ Diraclines with the (possibly complex) weights $X_1$, ... , $X_I$,
so applies to the transmission power taking into account the mirror-image lines at the negative frequencies:
- $$P_x = 2 \cdot \sum_{i=1}^I |X_k|^2.$$
(6) Correspondingly, the following applies to the distortion power if the spectral function $E(f)$ in the range $f>0$ has $J$ Diraclines with weights $E_1$, ... , $E_J$:
- $$P_\varepsilon = 2 \cdot \sum_{j=1}^J |E_j|^2.$$
Theoretical Background
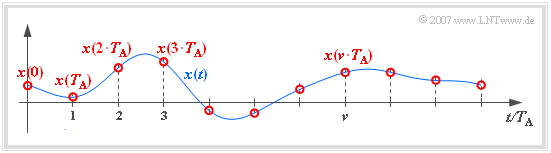
Description of sampling in the time domain
In the following, we use the following nomenclature to describe the sampling:
- let the continuous-time signal be $x(t)$.
- Let the time-discretized signal sampled at equidistant intervals $T_{\rm A}$ be $x_{\rm A}(t)$.
- Out of the sampling time points $\nu \cdot T_{\rm A}$ always holds $x_{\rm A}(t) \equiv 0$.
- The run variable $\nu$ be an "integer": $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $.
- In contrast, at the equidistant sampling times with the constant $K$, the result is:
- $$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$
The constant depends on the type of time discretization. For the above sketch $K = 1$ is valid.
Description of sampling with the Dirac delta pulse
In the following, we assume a slightly different form of description. The following pages will show that these equations, which take some getting used to, do lead to useful results if they are applied consistently.
$\text{Definitions:}$
- By sampling we mean here the multiplication of the time-continuous signal $x(t)$ by a Dirac delta pulse:
- $$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$
- The Dirac delta pulse (in the time domain) consists of infinitely many Dirac delta pulses, each equally spaced $T_{\rm A}$ and all with equal momentum weight $T_{\rm A}$:
- $$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
Based on this definition, the following properties result for the sampled signal:
- $$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
- The sampled signal at the considered time $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$.
- Since $\delta (t)$ at time $t = 0$ is infinite, actually all signal values $x_{\rm A}(\nu \cdot T_{\rm A})$ are also infinite and also the factor $K$ introduced above.
- Two samples $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ and $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ however, differ in the same proportion as the signal values $x(\nu_1 \cdot T_{\rm A})$ and $x(\nu_2 \cdot T_{\rm A})$.
- The samples of $x(t)$ appear in the momentum weights of the Dirac functions:
- The additional multiplication by $T_{\rm A}$ is necessary so that $x(t)$ and $x_{\rm A}(t)$ have the same unit. Note here that $\delta (t)$ itself has the unit "1/s".
Description of sampling in the frequency domain
Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des "Faltungssatzes". Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht:
- $$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$
Entwickelt man den Diracpuls $p_{\delta}(t)$ (im Zeitbereich) in eine "Fourierreihe" und transformiert diese unter Anwendung des "Verschiebungssatzes" in den Frequenzbereich, so ergibt sich mit dem Abstand $f_{\rm A} = 1/T_{\rm A}$ zweier benachbarter Diraclinien im Frequenzbereich folgende Korrespondenz ⇒ "Beweis":
- $$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ).$$
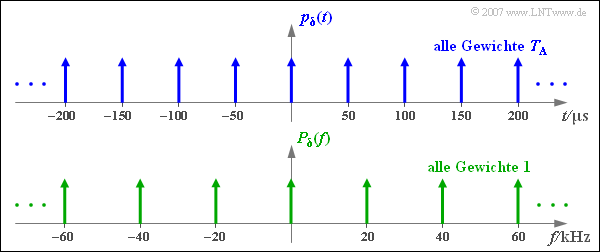
Das Ergebnis besagt:
- Der Diracpuls $p_{\delta}(t)$ im Zeitbereich besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$.
- Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$.
- Auch $P_{\delta}(f)$ besteht aus unendlich vielen Diracimpulsen, nun im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$.
- Die Abstände der Diraclinien in Zeit– und Frequenzbereich folgen demnach dem "Reziprozitätsgesetz": $T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$
Daraus folgt: Aus dem Spektrum $X(f)$ wird durch Faltung mit der um $\mu \cdot f_{\rm A}$ verschobenen Diraclinie:
- $$X(f) \star \delta (f- \mu \cdot f_{\rm A} )= X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$
Wendet man dieses Ergebnis auf alle Diraclinien des Diracpulses an, so erhält man schließlich:
- $$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$
$\text{Fazit:}$ Die Abtastung des analogen Zeitsignals $x(t)$ in äquidistanten Abständen $T_{\rm A}$ führt im Spektralbereich zu einer periodischen Fortsetzung von $X(f)$ mit dem Frequenzabstand $f_{\rm A} = 1/T_{\rm A}$.
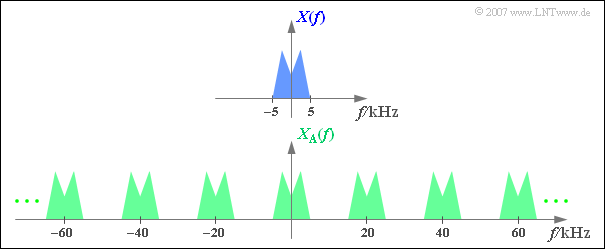
$\text{Beispiel 1:}$ Die obere Grafik zeigt (schematisch!) das Spektrum $X(f)$ eines Analogsignals $x(t)$, das Frequenzen bis $5 \text{ kHz}$ beinhaltet.
Tastet man das Signal mit der Abtastrate $f_{\rm A}\,\text{ = 20 kHz}$, also im jeweiligen Abstand $T_{\rm A}\, = {\rm 50 \, µs}$ ab, so erhält man das unten skizzierte periodische Spektrum $X_{\rm A}(f)$.
- Da die Diracfunktionen unendlich schmal sind, beinhaltet das abgetastete Signal $x_{\rm A}(t)$ auch beliebig hochfrequente Anteile.
- Dementsprechend ist die Spektralfunktion $X_{\rm A}(f)$ des abgetasteten Signals bis ins Unendliche ausgedehnt.
Signal reconstruction
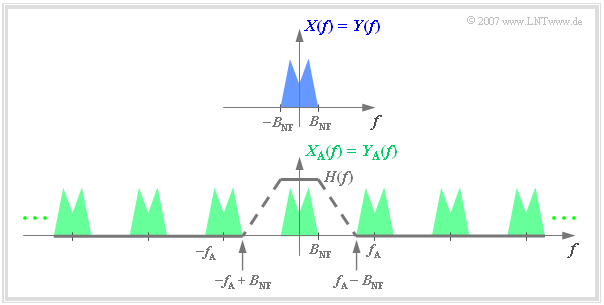
Die Signalabtastung ist bei einem digitalen Übertragungssystem kein Selbstzweck, sondern sie muss irgendwann wieder rückgängig gemacht werden. Betrachten wir zum Beispiel das folgende System:
- Das Analogsignal $x(t)$ mit der Bandbreite $B_{\rm NF}$ wird wie oben beschrieben abgetastet.
- Am Ausgang eines idealen Übertragungssystems liegt das ebenfalls zeitdiskrete Signal $y_{\rm A}(t) = x_{\rm A}(t)$ vor.
- Die Frage ist nun, wie der Block Signalrekonstruktion zu gestalten ist, damit auch $y(t) = x(t)$ gilt.
Die Lösung ist einfach, wenn man die Spektralfunktionen betrachtet:
Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch ein Tiefpass Filter mit dem "Frequenzgang" $H_{\rm E}(f)$, der
- die tiefen Frequenzen unverfälscht durchlässt:
- $$H_{\rm E}(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm NF}\hspace{0.05cm},$$
- die hohen Frequenzen vollständig unterdrückt:
- $$H_{\rm E}(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm NF}\hspace{0.05cm}.$$
Weiter ist aus der nebenstehenden Grafik zu erkennen: Solange die beiden oben genannten Bedingungen erfüllt sind, kann $H_{\rm E}(f)$ im Bereich von $B_{\rm NF}$ bis $f_{\rm A}–B_{\rm NF}$ beliebig geformt sein kann,
- beispielsweise linear abfallend (gestrichelter Verlauf)
- oder auch rechteckförmig,
The Sampling Theorem
Die vollständige Rekonstruktion des Analogsignals $y(t)$ aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ ist nur möglich, wenn die Abtastrate $f_{\rm A}$ entsprechend der Bandbreite $B_{\rm NF}$ des Nachrichtensignals richtig gewählt wurde.
Aus der obigen Grafik erkennt man, dass folgende Bedingung erfüllt sein muss: $f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$
$\text{Abtasttheorem:}$ Besitzt ein Analogsignal $x(t)$ nur Spektralanteile im Bereich $\vert f \vert < B_{\rm NF}$, so kann dieses aus seinem abgetasteten Signal $x_{\rm A}(t)$ nur dann vollständig rekonstruiert werden, wenn die Abtastrate hinreichend groß ist:
- $$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$$
Für den Abstand zweier Abtastwerte muss demnach gelten:
- $$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$$
Wird bei der Abtastung der größtmögliche Wert ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ herangezogen,
- so muss zur Signalrekonstruktion des Analogsignals aus seinen Abtastwerten
- ein idealer, rechteckförmiger Tiefpass mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ verwendet werden.
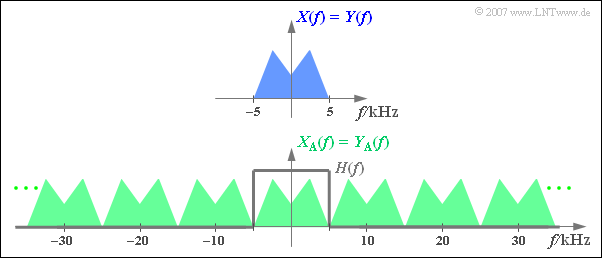
$\text{Beispiel 2:}$ Die Grafik zeigt oben das auf $\pm\text{ 5 kHz}$ begrenzte Spektrum $X(f)$ eines Analogsignals, unten das Spektrum $X_{\rm A}(f)$ des im Abstand $T_{\rm A} =\,\text{ 100 µs}$ abgetasteten Signals ⇒ $f_{\rm A}=\,\text{ 10 kHz}$.
Zusätzlich eingezeichnet ist der Frequenzgang $H_{\rm E}(f)$ des tiefpassartigen Empfangsfilters zur Signalrekonstruktion, dessen Grenzfrequenz exakt $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ betragen muss.
- Mit jedem anderen $f_{\rm G}$–Wert ergäbe sich $Y(f) \neq X(f)$.
- Bei $f_{\rm G} < 5\,\text{ kHz}$ fehlen die oberen $X(f)$–Anteile.
- Bei $f_{\rm G} > 5\,\text{ kHz}$ kommt es aufgrund von Faltungsprodukten zu unerwünschten Spektralanteilen in $Y(f)$.
Wäre am Sender die Abtastung mit einer Abtastrate $f_{\rm A} < 10\ \text{ kHz}$ erfolgt ⇒ $T_{\rm A} >100 \ {\rm µ s}$, so wäre das Analogsignal $y(t) = x(t)$ aus den Abtastwerten $y_{\rm A}(t)$ auf keinen Fall rekonstruierbar.
Exercises
- First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number $0$ corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution".
- All signal values are to be understood as normalized to $\pm 1$. Powers are normalized values, too.
(1) Source signal: $x(t) = A \cdot \cos (2\pi \cdot f_0 \cdot t -\varphi)$ with $f_0 = \text{4 kHz}$. Sampling with $f_{\rm A} = \text{10 kHz}$. Rectanglular low-pass; cut-off frequency: $f_{\rm G} = \text{5 kHz}$.
Interpret the shown graphics and evaluate the present signal reconstruction for all permitted parameter values of $A$ and $\varphi$.
- The spectrum $X(f)$ consists of two Dirac functions at $\pm \text{4 kHz}$, each with impulse weight $0.5$.
- By the periodic continuation $X_{\rm A}(f)$ has lines of equal height at $\pm \text{4 kHz}$, $\pm \text{6 kHz}$, $\pm \text{14 kHz}$, $\pm \text{16 kHz}$, $\pm \text{24 kHz}$, $\pm \text{26 kHz}$, etc.
- The rectangular low-pass with the cut-off frequency $f_{\rm G} = \text{5 kHz}$ removes all lines except the two at $\pm \text{4 kHz}$ ⇒ $Y(f) =X(f)$ ⇒ $y(t) =x(t)$ ⇒ $P_\varepsilon = 0$.
- The signal reconstruction works here perfectly $(P_\varepsilon = 0)$ for all amplitudes $A$ and any phases $\varphi$.
(2) Continue with $A=1$, $f_0 = \text{4 kHz}$, $\varphi=0$, $f_{\rm A} = \text{10 kHz}$, $f_{\rm G} = \text{5 kHz}$. What is the influence of the rolloff–factors $r=0.2$, $r=0.5$ and $r=1$?
Specify the power values $P_x$ and $P_\varepsilon$ . For which $r$–values is $P_\varepsilon= 0$? Do these results also apply to other $A$ and $\varphi$?
- With $|X(f = \pm \text{4 kHz})|=0.5$ the signal power is $P_x = 2\cdot 0.5^2 = 0.5$. The distortion power $P_\varepsilon$ depends significantly on the rolloff–factor $r$ .
- $P_\varepsilon$ is zero for $r \le 0.2$. Then the $X_{\rm A}(f)$ line at $f_0 = \text{4 kHz}$ is not changed by the low-pass and the unwanted line at $\text{6 kHz}$ is fully suppressed.
- $r = 0.5$ : $Y(f = \text{4 kHz}) = 0.35$, $Y(f = \text{6 kHz}) = 0.15$ ⇒ $|E(f = \text{4 kHz})| = |E(f = \text{6 kHz})|= 0. 15$ ⇒ $P_\varepsilon = 0.09$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=7.45\ \rm dB$.
- $r = 1.0$ : $Y(f = \text{4 kHz}) = 0.3$, $Y(f = \text{6 kHz}) = 0.2$ ⇒ $|E(f = \text{4 kHz})| = |E(f = \text{6 kHz})|= 0. 2$ ⇒ $P_\varepsilon = 0.16$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=4.95\ \rm dB$.
- For all $r$ the distortion power $P_\varepsilon$ is independent of $\varphi$. The amplitude $A$ affects $P_x$ and $P_\varepsilon$ in the same way ⇒ the quotient is independent of $A$.
(3) Now apply $A=1$, $f_0 = \text{5 kHz}$, $\varphi=0$, $f_{\rm A} = \text{10 kHz}$, $f_{\rm G} = \text{5 kHz}$, $r=0$ $($rectangular low–pass$)$. Interpret the result of the signal reconstruction.
- $X(f)$ consists of two Dirac delta lines at $\pm \text{5 kHz}$ $($weight $0.5)$. By periodic continuation $X_{\rm A}(f)$ has lines at $\pm \text{5 kHz}$, $\pm \text{15 kHz}$, $\pm \text{25 kHz}$, etc.
- The rectanglular low-pass removes the lines at $\pm \text{15 kHz}$, $\pm \text{25 kHz}$. The lines at $\pm \text{5 kHz}$ are halved because of $H_{\rm E}(\pm f_{\rm G}) = H_{\rm E}(\pm \text{5 kHz}) = 0.5$.
- ⇒ $\text{Weights of }X(f = \pm \text{5 kHz})$: $0.5$ # $\text{Weights of }X(f_{\rm A} = \pm \text{5 kHz})$: $1. 0$; # $\text{Weights of }Y(f = \pm \text{5 kHz})$: $0.5$ ⇒ $Y(f)=X(f)$.
- So the signal reconstruction works perfectly here too $(P_\varepsilon = 0)$. The same is true for the phase $\varphi=180^\circ$ ⇒ $x(t) = -A \cdot \cos (2\pi \cdot f_0 \cdot t)$.
(4) The settings of $(3)$ continue to apply except for $\varphi=30^\circ$. Interpret the differences from the setting $(3)$ ⇒ $\varphi=0^\circ$.
- Phase relations are lost. The sink signal $y(t)$ is cosine-shaped $(\varphi_y=0^\circ)$ with by the factor $\cos(\varphi_x)$ smaller amplitude than the source signal $x(t)$.
- Justification in the frequency domain: In the periodic continuation of $X(f)$ ⇒ $X_{\rm A}(f)$ only the real parts are to be added. The imaginary parts cancel out.
- The Dirac delta line of $X(f)$ at frequency $f_0$ ⇒ $X(f_0)$ is complex, $Y(f_0)$ is real, and $E(f_0)$ is imaginary ⇒ $\varepsilon(t)$ is minus–sinusoidal ⇒ $P_\varepsilon = 0. 125$.
(5) Illustrate again the result of $(4)$ compared to the settings $f_0 = \text{5 kHz}$, $\varphi=30^\circ$, $f_{\rm A} = \text{11 kHz}$, $f_{\rm G} = \text{5.5 kHz}$.
- With this setting, the spectrum $X_{\rm A}(f)$ also has a positive imaginary part at $\text{5 kHz}$ and a negative imaginary part of the same magnitude at $\text{6 kHz}$.
- The rectangular low-pass with cutoff frequency $\text{5.5 kHz}$ removes this second component. Thus, with the new setting $Y(f) =X(f)$ ⇒ $P_\varepsilon = 0$.
- Any $f_0$ oscillation of arbitrary phase is error-free reconstructible from its samples if $f_{\rm A} = 2 \cdot f_{\rm 0} + \mu, \ f_{\rm G}= f_{\rm A}/2$ $($any small $\mu>0)$.
- For value–continuous spectrum with $X(|f|> f_0) \equiv 0$ ⇒ $\big[$no diraclines at $\pm f_0 \big ]$ the sampling rate $f_{\rm A} = 2 \cdot f_{\rm 0}$ is sufficient in principle.
(5) Verdeutlichen Sie sich nochmals das Ergebnis von (4) im Vergleich zu den Einstellungen $f_0 = \text{5 kHz}$, $\varphi=30^\circ$, $f_{\rm A} = \text{11 kHz}$, $f_{\rm G} = \text{5.5 kHz}$.
- Bei dieser Einstellung hat das $X_{\rm A}(f)$–Spektrum auch einen positiven Imaginärteil bei $\text{5 kHz}$ und einen negativen Imaginärteil gleicher Höhe bei $\text{6 kHz}$.
- Der Rechteck–Tiefpass mit der Grenzfrequenz $\text{5.5 kHz}$ entfernt diesen zweiten Anteil. Somit ist bei dieser Einstellung $Y(f) =X(f)$ ⇒ $P_\varepsilon = 0$.
- Jede $f_0$–Schwingung beliebiger Phase ist fehlerfrei aus seinen Abtastwerten rekonstruierbar, falls $f_{\rm A} = 2 \cdot f_{\rm 0} + \mu, \ f_{\rm G}= f_{\rm A}/2$ $($beliebig kleines $\mu>0)$.
- Bei wertkontinuierlichem Spektrum mit $X(|f|> f_0) \equiv 0$ ⇒ $\big[$keine Diraclinien bei $\pm f_0 \big ]$ genügt grundsätzlich die Abtastrate $f_{\rm A} = 2 \cdot f_{\rm 0}$.
(6) The settings of $(3)$ and $(4)$ continue to apply except for $\varphi=90^\circ$. Interpret the plots in the time and frequency domain.
- The source signal is sampled exactly at its zero crossings ⇒ $x_{\rm A}(t) \equiv 0$ ⇒ $y(t) \equiv 0$ ⇒ $\varepsilon(t)=-x(t)$ ⇒ $P_\varepsilon = P_x$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=0\ \rm dB$.
- Description in the frequency domain: As in $(4)$ the imaginary parts of $X_{\rm A}(f)$ cancel out. Also the real parts of $X_{\rm A}(f)$ are zero because of the sinusoid.
(7) Now consider the $\text {Source Signal 2}$. Let the other parameters be $f_{\rm A} = \text{5 kHz}$, $f_{\rm G} = \text{2.5 kHz}$, $r=0$. Interpret the results.
- The source signal has spectral components up to $\pm \text{2 kHz}$. The signal power is $P_x = 2 \cdot \big[0.1^2 + 0.25^2+0.15^2\big]= 0.19 $.
- With the sampling rate $f_{\rm A} = \text{5 kHz}$ and the receiver parameters $f_{\rm G} = \text{2.5 kHz}$ and $r=0$, the signal reconstruction works perfectly: $P_\varepsilon = 0$.
- Likewise with the trapezoidal low–pass with $f_{\rm G} = \text{2.5 kHz}$, if for the rolloff factor holds: $r \le 0.2$.
(8) What happens if the cutoff frequency $f_{\rm G} = \text{1.5 kHz}$ of the rectangular low–pass filter is too small? In particular, interpret the error signal $\varepsilon(t)=y(t)-x(t)$.
- The error signal $\varepsilon(t)=-0.3 \cdot \cos(2\pi \cdot \text{2 kHz} \cdot t -60^\circ)=0. 3 \cdot \cos(2\pi \cdot \text{2 kHz} \cdot t +120^\circ)$ is equal to the (negated) signal component at $\text{2 kHz}$.
- The distortion power is $P_\varepsilon=2 \cdot 0.15^2= 0.045$ and the signal–to–distortion ratio $10 \cdot \lg \ (P_x/P_\varepsilon)=10 \cdot \lg \ (0.19/0.045)= 6.26\ \rm dB$.
(9) What happens if the cutoff frequency $f_{\rm G} = \text{3.5 kHz}$ of the rectangular low–pass filter is too large? In particular, interpret the error signal $\varepsilon(t)=y(t)-x(t)$.
- The error signal $\varepsilon(t)=0.3 \cdot \cos(2\pi \cdot \text{3 kHz} \cdot t +60^\circ)$ is now equal to the $\text{3 kHz}$ portion of the sink signal $y(t)$ not removed by the low-pass filter.
- Compared to the subtask $(8)$ the frequency changes from $\text{2 kHz}$ to $\text{3 kHz}$ and also the phase relationship.
- The amplitude of this $\text{3 kHz}$ error signal is equal to the amplitude of the $\text{2 kHz}$ portion of $x(t)$. Again $P_\varepsilon= 0.045$, $10 \cdot \lg \ (P_x/P_\varepsilon)= 6.26\ \rm dB$.
(10) Finally, we consider the $\text {source signal 4}$ $($portions until $\pm \text{4 kHz})$, as well as $f_{\rm A} = \text{5 kHz}$, $f_{\rm G} = \text{2. 5 kHz}$, $0 \le r\le 1$. Interpretation of results.
- Up to $r=0.2$ the signal reconstruction works perfectly $(P_\varepsilon = 0)$. If one increases $r$, then $P_\varepsilon$ increases continuously and $10 \cdot \lg \ (P_x/P_\varepsilon)$ decreases.
- With $r=1$ the signal frequencies $\text{0.5 kHz}$, ..., $\text{4 kHz}$ are attenuated, the more the higher the frequency is, for example $H_{\rm E}(f=\text{4 kHz}) = 0.6$.
- Similarly, $Y(f)$ also includes components at frequencies $\text{6 kHz}$, $\text{7 kHz}$, $\text{8 kHz}$, $\text{9 kHz}$ and $\text{9.5 kHz}$ due to periodic continuation.
- At the sampling times $t\hspace{0.05cm}' = n \cdot T_{\rm A}$, the signals $x(t\hspace{0.05cm}')$ and $y(t\hspace{0.05cm}')$ agree exactly ⇒ $\varepsilon(t\hspace{0.05cm}') = 0$. In between, not ⇒ small distortion power $P_\varepsilon = 0.008$.
Applet Manual
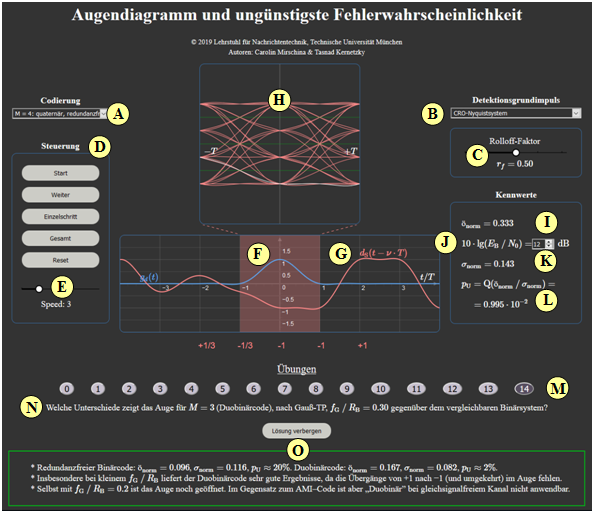
(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)
(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}
(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)
(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)
(E) Geschwindigkeit der Augendiagrammdarstellung
(F) Darstellung: Detektionsgrundimpuls $g_d(t)$
(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$
(H) Darstellung: Augendiagramm im Bereich $\pm T$
( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)
(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)
(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)
(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)
(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(N) Bereich für die Versuchsdurchführung: Aufgabenstellung
(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2008 by Slim Lamine as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- Last revision and English version 2020/2021 by Carolin Mirschina in the context of a working student activity.
The conversion of this applet to HTML 5 was financially supported by Studienzuschüsse ("study grants") of the TUM Faculty EI. We thank.