Difference between revisions of "Digital Signal Transmission/Applications for Multimedia Files"
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{LastPage}} | {{LastPage}} | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Digital Channel Models |
|Vorherige Seite=Bündelfehlerkanäle | |Vorherige Seite=Bündelfehlerkanäle | ||
|Nächste Seite= | |Nächste Seite= | ||
}} | }} | ||
| − | == | + | == Images in BMP format == |
<br> | <br> | ||
| − | + | One of the oldest image formats is the so-called "'''bitmap format'''". Corresponding files are marked with the extension "bmp". | |
| − | |||
| − | * | + | Essential properties of BMP images are: |
| + | *A bitmap is a matrix of pixels, whose individual elements are also called pixels $($"picture elements"$)$. The pixels are stored line by line, from bottom right to top left.<br> | ||
| − | * | + | *Each pixel is also assigned an RGB color value from the additive primary colors "$\rm r$ed", "$\rm g$reen" and "$\rm b$lue". The larger the color value can be, the finer the colors to be displayed can be graded.<br> |
| − | * | + | *The color depth of an image is specified in ''bits per pixel'' (BPP). Common color depths are $1$ (black and white image), $4$, $8$ and $24$ (true color image).<br> |
| + | *Since most images do not use the entire color spectrum, it is possible to define a specific assignment in each bitmap in the form of a color table. This way, even with relatively low color depth (up to eight bits), the images can be displayed with good color quality.<br> | ||
| − | |||
| − | + | [[File:P ID1851 Dig T 5 4 S1 version1.png|right|frame|Hexdump of a BMP file|class=fit]] | |
| − | |||
| − | * | + | Each BMP file consists of three sub-blocks, as the adjacent graphic illustrates: |
| + | *the file header (14 bytes),<br> | ||
| − | * | + | *the information block (at least 40 bytes), and finally<br> |
| − | + | *the image data block.<br><br> | |
| − | + | Shown are the first 160 bytes of the file "LNTprofs.bmp". The file header (in hexadecimal representation from 0x00 to 0x0D) as well as the image data area (from 0x36) are highlighted in yellow. Not highlighted is the 40 byte information block (from 0x0E to 0x35).<br> | |
| − | |||
| − | * | + | The '''file header''' contains the following information (the prefix "0x" indicates the hexadecimal representation and the trailing "d" indicates the decimal representation): |
| + | *0x00 ... 0x01 (2 bytes) BMP identifier: 0x 42 4D ⇒ "BM",<br> | ||
| − | * | + | *0x02 ... 0x05 (4 bytes) file size in bytes: 0x 02 DE 98 ⇒ 188056d,<br> |
| − | * | + | *0x06 ... 0x09 (5 bytes) reserved (must always be filled with zeros),<br> |
| − | + | *0x0A ... 0x0D (4 bytes) offset (start of image data): 0x 00 00 00 36 ⇒ 54d.<br><br> | |
| − | + | <i>Note:</i> However, these specifications only apply to the Intel processor, which reads according to the so-called <i>little–endian byte order</i> from the least significant byte (LSB) to the most significant byte (MSB). The order "98 DE 02 00" of bytes 2, ..., 5 is thus to be interpreted as "0x 00 02 DE 98", which corresponds to the decimal number "188056".<br> | |
| − | |||
| − | * | + | The '''40 byte information block''' contains the following values (bytes with the content "00" are not specified here): |
| + | *0x0E ... 0x11 (4 bytes) Length of info block: 0x 28 ⇒ 40d,<br> | ||
| − | * | + | *0x12 ... 0x15 (4 bytes) Image width in pixels: 0x FA ⇒ 250d,<br> |
| − | * | + | *0x16 ... 0x19 (4 bytes) Image height in pixels: 0x FA ⇒ 250d,<br> |
| − | * | + | *0x1A ... 0x1B (2 bytes) Number of color planes (always set to 1),<br> |
| − | * | + | *0x1C ... 0x1D (2 bytes) Bits per pixel (BPP): 0x0018 ⇒ 24d,<br> |
| − | * | + | *0x1E ... 0x21 (4 bytes) Type of data compression,<br> |
| − | * | + | *0x22 ... 0x25 (4 bytes) Size of bitmap in bytes: 0x 02 DE 62 ⇒ 188002d,<br> |
| − | * | + | *0x26 ... 0x29 (4 bytes) Horizontal resolution in pixels/meter: 0x 26 70 ⇒ 9840d,<br> |
| − | * | + | *0x2A ... 0x2D (4 bytes) Vertical resolution in pixels/meter: 0x 26 70 ⇒ 9840d,<br> |
| − | * | + | *0x2E ... 0x31 (4 bytes) Number of colors used,<br> |
| − | + | *0x32 ... 0x35 (4 bytes) Number of important colors.<br><br> | |
| − | + | Then the '''image data area''' begins with "0x 43 2A 23" (in the example three bytes per pixel each for R – G – B). Since also here (with the Intel processor) the <i>little–endian byte order</i> applies, these entries designate the color values $\rm R = 23$, $\rm G = 2A$, $\rm B = 43$ (in each case hexadecimal) or $\rm R = 35$, $\rm G = 42$, $\rm B = 67$ (decimal) .<br> | |
| − | == | + | The images in the next section make it clear that even a few errors in the file header ($14$ bytes) or information block ($40$ bytes) are enough to render an image completely unusable. The header of a multimedia file should therefore be specially protected. In the case of BMP, this header comprises a total of $54$ bytes.<br> |
| + | |||
| + | == Transmission errors in the file header and information block == | ||
<br> | <br> | ||
| − | + | A series of images is used to illustrate the effects of transmission errors within the file header (0x00 ... 0x0D) and information block (0x0E ... 0x35). The left figure shows the hexadecimal dump of the falsified file compared to the original file (right).<br> | |
| − | [[File: | + | [[File:EN_Dig_T_5_4_S2a_v3.png|center|frame|Hexdumps of the falsified file and the original file|class=fit]] |
| − | + | Below you can see the images that result when the five error blocks are successively corrected: | |
| − | [[File: | + | [[File:EN_Dig_T_5_4_S2b.png|right|frame|Effects of errors in the BMP header|class=fit]] |
| − | |||
| − | * | + | *The given file cannot be opened at all. If we correct the first two bytes (purple marking) from "0x 40 00" to "0x 42 4D", we get the upper left uniform gray image.<br> |
| − | * | + | *Correcting the image width from "0x C5" to "0x FA" ⇒ 250d and the image height from "0x 7D" to "0x FA" ⇒ 250d (green mark) results in the middle upper image already with the correct size (250 x 250 pixels), but still with gray content.<br> |
| − | * | + | *The upper right image can be reached by correcting the color depth (''bits per pixel'', BPP) from "0x 08" ⇒ 8d to "0x 18" ⇒ 24d (blue mark). After that, one can already partially recognize content, but with poor quality.<br> |
| + | |||
| + | *By correcting the red error block in the range 0x0A ... 0x0D (offset) from "0x 36 01" to "0x 36 00" you finally get the original image "LNTprofs.bmp". | ||
<br clear=all> | <br clear=all> | ||
| − | + | == BMP files after BSC falsification== | |
| − | |||
| − | == | ||
<br> | <br> | ||
| − | + | The following series of images shows the influence of statistically independent errors (BSC model) with the following (bit) error probabilities: | |
| − | + | :$$p = 10^{-3}, \ p = 10^{-2}, \ p = 10^{-1}.$$ | |
| − | :$$p = 10^{-3}, \ p = 10^{-2}, \ p = 10^{-1}$. | + | [[File:Dig_T_5_4_S3_version2.png|right|frame|Influence of BSC errors on BMP files, above with 24 BPP, below with 8 BPP|class=fit]] |
| − | + | The file header is error-free in each case.<br> | |
| − | * | + | *The upper row is based on the color image "LNTprofs.bmp" with $\rm 24$ bits per pixel; the actual image area is $250 \cdot 250 \cdot 24 = 1.5 \cdot 10^6$ bits. |
| − | * | + | *The bottom row is based on a grayscale image with $\rm 8$ bits per pixel. The file is thus about a factor of $3$ smaller than the color file. |
| − | |||
| − | |||
| − | |||
| − | * | + | One recognizes from these representations: |
| + | *The error probability $p = 10^{-3}$ is still not too disturbing. With the color image, about $1500$ bits and also comparatively as many pixels are falsified (statistical statements). With the grayscale image, there are only about $500$ bit errors because of the smaller file.<br> | ||
| − | == | + | *Subjectively, the disturbing impression of bit errors with the grayscale image is about the same as with the color image, despite the smaller number of bit errors, since with the latter some bit errors only have an effect in a marginal color change.<br> |
| + | <br clear=all> | ||
| + | == BMP files with burst errors == | ||
<br> | <br> | ||
| − | + | Let's now look at the influence of burst errors on BMP files using the following graphic. | |
| + | |||
| + | *The left image $\rm A$ shows the original file "Weiß.bmp" with only white pixels. | ||
| + | *The result is therefore independent of the color depth. | ||
| + | *However, the file "Weiß1.bmp" (1 BPP, 4046 bytes) is almost by a factor of $24$ smaller than the file "Weiß24.bmp" (24 BPP, 90456 bytes). | ||
| + | *Almost because the header is the same size for both files and the $\text{1 BPP}$ file also contains a color table.<br> | ||
| − | [[File: | + | <br clear=all> |
| + | For the four right images, transmission errors with the (average) error probability $p_{\rm M} = 1\%$ are considered in each case. One recognizes: | ||
| + | [[File:EN_Dig_T_5_4_S4.png|right|frame|Influence of burst errors on BMP files|class=fit]] | ||
| − | + | *The errors in image $\rm B$ are statistically independent and were generated according to the [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)|"BSC model"]]. They are randomly distributed over the whole image area.<br> | |
| − | |||
| − | * | + | *In contrast, images $\rm C$ and $\rm D$ show burst error structures according to the [[Digital_Signal_Transmission/Burst_Error_Channels#Channel_model_according_to_Gilbert-Elliott|"GE model"]] with different error correlation durations $D_{\rm K} \approx 8$ and $D_{\rm K} \approx 95$. It can be seen from the error structure that BMP images are saved line by line.<br> |
| − | * | + | *For the black and white images (1 BPP) $\rm B$, $\rm C$ and $\rm D$, every 100th pixel is falsified on statistical average. In contrast, image $\rm E$ with 24 BPP (''True Color'') has more pixel falsifications despite the same average error probability $p_{\rm M} = 1\%$. <br> |
| − | * | + | *A comparison of images $\rm D$ and $\rm E$ shows the different correlation durations related to pixels $(D_{\rm K} \approx 95$ versus $D_{\rm K} \approx 95/24 \approx 4)$. It can also be seen that in image $\rm E$ the error pixels are colored.<br><br> |
| − | == | + | == Effects of transmission errors on audios == |
<br> | <br> | ||
| − | + | The [https://en.wikipedia.org/wiki/WAV "WAVE file format"] is a container format for digital storage of audio data, based on the ''Resource Interchange File Format'' (RIFF) defined by Microsoft for Windows. The file header of WAVE files, which requires special protection, comprises $43$ bytes. | |
| − | + | It usually contains so-called PCM raw data, i.e. a time- and value-discrete representation of the temporal course of a signal. The quality of the recorded sound then depends on two values, namely | |
| − | * | + | *the sampling rate (number of samples per time unit), |
| − | * | + | *the resolution (bit depth). |
| − | + | We will first demonstrate the influence of transmission errors on the audio file "Stille.wav" with a duration of about 10 seconds. That means: All you hear are transmission errors. | |
| − | ''' | + | '''Statistically independent errors according to the BSC model''' |
| − | + | For the following WAVE files we start with the [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)|"BSC parameter"]] $p= 10^{-5}$ and increase it up to $p= 10\%$. | |
| + | *$p$ indicates at the same time the average error probability $p_{\rm M}$, which is also called <i>Bit Error Rate</i> (BER). | ||
| + | *In each case, the author's subjective assessment is also indicated.<br> | ||
| − | <lntmedia>file:A_ID41__ruhe1_bsc_00001.mp3</lntmedia> $p=10^{-5}$ ⇒ | + | <lntmedia>file:A_ID41__ruhe1_bsc_00001.mp3</lntmedia> $p=10^{-5}$ ⇒ Barely audible. <br><br> |
| − | <lntmedia>file:A_ID43__ruhe1_bsc_0001.mp3</lntmedia> $p=10^{-4}$ ⇒ | + | <lntmedia>file:A_ID43__ruhe1_bsc_0001.mp3</lntmedia> $p=10^{-4}$ ⇒ Not yet very disturbing. <br><br> |
| − | <lntmedia>file:A_ID44__ruhe1_bsc_001.mp3</lntmedia> $p=10^{-3}$ ⇒ | + | <lntmedia>file:A_ID44__ruhe1_bsc_001.mp3</lntmedia> $p=10^{-3}$ ⇒ Noticeably disturbing. <br><br> |
| − | <lntmedia>file:A_ID45__ruhe1_bsc_01.mp3</lntmedia> $p=10^{-2}$ ⇒ | + | <lntmedia>file:A_ID45__ruhe1_bsc_01.mp3</lntmedia> $p=10^{-2}$ ⇒ Warning before opening.<br><br> |
| − | <lntmedia>file:A_ID46__ruhe1_bsc_1.mp3</lntmedia> $p=10^{-1}$ ⇒ | + | <lntmedia>file:A_ID46__ruhe1_bsc_1.mp3</lntmedia> $p=10^{-1}$ ⇒ Only suitable for those extremely insensitive to noise.<br><br> |
| − | ''' | + | '''Comparison of statistically independent errors and burst errors''' |
| − | * | + | *The statistically independent errors were again generated using the [[Digital_Signal_Transmission/Binary_Symmetric_Channel_(BSC)|"BSC model"]]. Mean error probability: $p_{\rm M}=10^{-3}$. |
| − | * | + | *For the generation of the burst errors, the [[Digital_Signal_Transmission/Burst_Error_Channels#Channel_model_according_to_Gilbert-Elliott|"Gilbert–Elliott"]] (GE) channel model was used. |
| − | * | + | *The mean error probability here is also $p_{\rm M}=10^{-3}$. |
| − | * | + | *Contrast this with the very short [[Digital_Signal_Transmission/Burst_Error_Channels#Error_correlation_function_of_the_Gilbert-Elliott_model|"correlation period"]] $D_{\rm K}= 8$ with long-range statistical ties ⇒ $D_{\rm K}= 1000$. |
| − | + | First, we start again from the file "Stille.wav". We can see that a short error correlation duration of the GE model in the result is not too different from statistically independent errors, since each sample is represented with $16$ bits. | |
| − | <lntmedia>file:A_ID43__ruhe1_bsc_0001.mp3</lntmedia> BSC | + | <lntmedia>file:A_ID43__ruhe1_bsc_0001.mp3</lntmedia> BSC model. <br><br> |
| − | <lntmedia>file:A_ID51__ruhe1_ge_8.mp3</lntmedia> GE | + | <lntmedia>file:A_ID51__ruhe1_ge_8.mp3</lntmedia> GE model with $D_{\rm K}= 8$. <br><br> |
| − | <lntmedia>file:A_ID52__ruhe1_ge_1000.mp3</lntmedia> GE | + | <lntmedia>file:A_ID52__ruhe1_ge_1000.mp3</lntmedia> GE model with $D_{\rm K}= 1000$.<br><br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The same channel parameters also apply to the following short piece of music and one recognizes similar characteristics.<br> | ||
| + | <lntmedia>file:A_ID48__k2_bsc.mp3</lntmedia> BSC model. <br><br> | ||
| + | <lntmedia>file:A_ID53__k2_ge_8.mp3</lntmedia> GE model with $D_{\rm K}= 8$. <br><br> | ||
| + | <lntmedia>file:A_ID54__k2_ge_1000.mp3</lntmedia> GE model with $D_{\rm K}= 1000$.<br><br> | ||
| + | ''Note'': All ( falsified ) BMP images and WAV audios for this chapter were generated with the Windows program "Digital Channel Models & Multimedia" from the (former) practical course "Simulation of Digital Transmission Systems" at the Chair of Communications Engineering of the TU Munich. The following links provide: | ||
| + | *the Windows program [http://en.lntwww.de/downloads/Sonstiges/Programme/DKM.zip DKM] ⇒ link refers to the ZIP version of the program; and | ||
| + | *the corresponding [http://en.lntwww.de/downloads/Sonstiges/Texte/Digitale_Kanalmodelle.pdf lab manual] ⇒ link refers to the PDF version. | ||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_5.8:_BMP_Format|Exercise 5.8: BMP Format]] |
| − | [[ | + | [[Aufgaben:Exercise_5.8Z:_Falsification_of_BMP_Images|Exercise 5.8Z: Falsification of BMP Images]] |
{{Display}} | {{Display}} | ||
Latest revision as of 12:54, 17 April 2023
Contents
Images in BMP format
One of the oldest image formats is the so-called "bitmap format". Corresponding files are marked with the extension "bmp".
Essential properties of BMP images are:
- A bitmap is a matrix of pixels, whose individual elements are also called pixels $($"picture elements"$)$. The pixels are stored line by line, from bottom right to top left.
- Each pixel is also assigned an RGB color value from the additive primary colors "$\rm r$ed", "$\rm g$reen" and "$\rm b$lue". The larger the color value can be, the finer the colors to be displayed can be graded.
- The color depth of an image is specified in bits per pixel (BPP). Common color depths are $1$ (black and white image), $4$, $8$ and $24$ (true color image).
- Since most images do not use the entire color spectrum, it is possible to define a specific assignment in each bitmap in the form of a color table. This way, even with relatively low color depth (up to eight bits), the images can be displayed with good color quality.
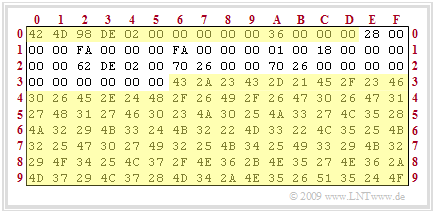
Each BMP file consists of three sub-blocks, as the adjacent graphic illustrates:
- the file header (14 bytes),
- the information block (at least 40 bytes), and finally
- the image data block.
Shown are the first 160 bytes of the file "LNTprofs.bmp". The file header (in hexadecimal representation from 0x00 to 0x0D) as well as the image data area (from 0x36) are highlighted in yellow. Not highlighted is the 40 byte information block (from 0x0E to 0x35).
The file header contains the following information (the prefix "0x" indicates the hexadecimal representation and the trailing "d" indicates the decimal representation):
- 0x00 ... 0x01 (2 bytes) BMP identifier: 0x 42 4D ⇒ "BM",
- 0x02 ... 0x05 (4 bytes) file size in bytes: 0x 02 DE 98 ⇒ 188056d,
- 0x06 ... 0x09 (5 bytes) reserved (must always be filled with zeros),
- 0x0A ... 0x0D (4 bytes) offset (start of image data): 0x 00 00 00 36 ⇒ 54d.
Note: However, these specifications only apply to the Intel processor, which reads according to the so-called little–endian byte order from the least significant byte (LSB) to the most significant byte (MSB). The order "98 DE 02 00" of bytes 2, ..., 5 is thus to be interpreted as "0x 00 02 DE 98", which corresponds to the decimal number "188056".
The 40 byte information block contains the following values (bytes with the content "00" are not specified here):
- 0x0E ... 0x11 (4 bytes) Length of info block: 0x 28 ⇒ 40d,
- 0x12 ... 0x15 (4 bytes) Image width in pixels: 0x FA ⇒ 250d,
- 0x16 ... 0x19 (4 bytes) Image height in pixels: 0x FA ⇒ 250d,
- 0x1A ... 0x1B (2 bytes) Number of color planes (always set to 1),
- 0x1C ... 0x1D (2 bytes) Bits per pixel (BPP): 0x0018 ⇒ 24d,
- 0x1E ... 0x21 (4 bytes) Type of data compression,
- 0x22 ... 0x25 (4 bytes) Size of bitmap in bytes: 0x 02 DE 62 ⇒ 188002d,
- 0x26 ... 0x29 (4 bytes) Horizontal resolution in pixels/meter: 0x 26 70 ⇒ 9840d,
- 0x2A ... 0x2D (4 bytes) Vertical resolution in pixels/meter: 0x 26 70 ⇒ 9840d,
- 0x2E ... 0x31 (4 bytes) Number of colors used,
- 0x32 ... 0x35 (4 bytes) Number of important colors.
Then the image data area begins with "0x 43 2A 23" (in the example three bytes per pixel each for R – G – B). Since also here (with the Intel processor) the little–endian byte order applies, these entries designate the color values $\rm R = 23$, $\rm G = 2A$, $\rm B = 43$ (in each case hexadecimal) or $\rm R = 35$, $\rm G = 42$, $\rm B = 67$ (decimal) .
The images in the next section make it clear that even a few errors in the file header ($14$ bytes) or information block ($40$ bytes) are enough to render an image completely unusable. The header of a multimedia file should therefore be specially protected. In the case of BMP, this header comprises a total of $54$ bytes.
Transmission errors in the file header and information block
A series of images is used to illustrate the effects of transmission errors within the file header (0x00 ... 0x0D) and information block (0x0E ... 0x35). The left figure shows the hexadecimal dump of the falsified file compared to the original file (right).
Below you can see the images that result when the five error blocks are successively corrected:
- The given file cannot be opened at all. If we correct the first two bytes (purple marking) from "0x 40 00" to "0x 42 4D", we get the upper left uniform gray image.
- Correcting the image width from "0x C5" to "0x FA" ⇒ 250d and the image height from "0x 7D" to "0x FA" ⇒ 250d (green mark) results in the middle upper image already with the correct size (250 x 250 pixels), but still with gray content.
- The upper right image can be reached by correcting the color depth (bits per pixel, BPP) from "0x 08" ⇒ 8d to "0x 18" ⇒ 24d (blue mark). After that, one can already partially recognize content, but with poor quality.
- By correcting the red error block in the range 0x0A ... 0x0D (offset) from "0x 36 01" to "0x 36 00" you finally get the original image "LNTprofs.bmp".
BMP files after BSC falsification
The following series of images shows the influence of statistically independent errors (BSC model) with the following (bit) error probabilities:
- $$p = 10^{-3}, \ p = 10^{-2}, \ p = 10^{-1}.$$
The file header is error-free in each case.
- The upper row is based on the color image "LNTprofs.bmp" with $\rm 24$ bits per pixel; the actual image area is $250 \cdot 250 \cdot 24 = 1.5 \cdot 10^6$ bits.
- The bottom row is based on a grayscale image with $\rm 8$ bits per pixel. The file is thus about a factor of $3$ smaller than the color file.
One recognizes from these representations:
- The error probability $p = 10^{-3}$ is still not too disturbing. With the color image, about $1500$ bits and also comparatively as many pixels are falsified (statistical statements). With the grayscale image, there are only about $500$ bit errors because of the smaller file.
- Subjectively, the disturbing impression of bit errors with the grayscale image is about the same as with the color image, despite the smaller number of bit errors, since with the latter some bit errors only have an effect in a marginal color change.
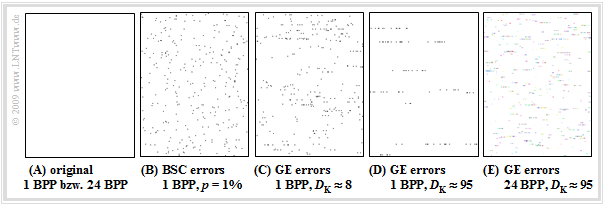
BMP files with burst errors
Let's now look at the influence of burst errors on BMP files using the following graphic.
- The left image $\rm A$ shows the original file "Weiß.bmp" with only white pixels.
- The result is therefore independent of the color depth.
- However, the file "Weiß1.bmp" (1 BPP, 4046 bytes) is almost by a factor of $24$ smaller than the file "Weiß24.bmp" (24 BPP, 90456 bytes).
- Almost because the header is the same size for both files and the $\text{1 BPP}$ file also contains a color table.
For the four right images, transmission errors with the (average) error probability $p_{\rm M} = 1\%$ are considered in each case. One recognizes:
- The errors in image $\rm B$ are statistically independent and were generated according to the "BSC model". They are randomly distributed over the whole image area.
- In contrast, images $\rm C$ and $\rm D$ show burst error structures according to the "GE model" with different error correlation durations $D_{\rm K} \approx 8$ and $D_{\rm K} \approx 95$. It can be seen from the error structure that BMP images are saved line by line.
- For the black and white images (1 BPP) $\rm B$, $\rm C$ and $\rm D$, every 100th pixel is falsified on statistical average. In contrast, image $\rm E$ with 24 BPP (True Color) has more pixel falsifications despite the same average error probability $p_{\rm M} = 1\%$.
- A comparison of images $\rm D$ and $\rm E$ shows the different correlation durations related to pixels $(D_{\rm K} \approx 95$ versus $D_{\rm K} \approx 95/24 \approx 4)$. It can also be seen that in image $\rm E$ the error pixels are colored.
Effects of transmission errors on audios
The "WAVE file format" is a container format for digital storage of audio data, based on the Resource Interchange File Format (RIFF) defined by Microsoft for Windows. The file header of WAVE files, which requires special protection, comprises $43$ bytes.
It usually contains so-called PCM raw data, i.e. a time- and value-discrete representation of the temporal course of a signal. The quality of the recorded sound then depends on two values, namely
- the sampling rate (number of samples per time unit),
- the resolution (bit depth).
We will first demonstrate the influence of transmission errors on the audio file "Stille.wav" with a duration of about 10 seconds. That means: All you hear are transmission errors.
Statistically independent errors according to the BSC model
For the following WAVE files we start with the "BSC parameter" $p= 10^{-5}$ and increase it up to $p= 10\%$.
- $p$ indicates at the same time the average error probability $p_{\rm M}$, which is also called Bit Error Rate (BER).
- In each case, the author's subjective assessment is also indicated.
$p=10^{-5}$ ⇒ Barely audible.
$p=10^{-4}$ ⇒ Not yet very disturbing.
$p=10^{-3}$ ⇒ Noticeably disturbing.
$p=10^{-2}$ ⇒ Warning before opening.
$p=10^{-1}$ ⇒ Only suitable for those extremely insensitive to noise.
Comparison of statistically independent errors and burst errors
- The statistically independent errors were again generated using the "BSC model". Mean error probability: $p_{\rm M}=10^{-3}$.
- For the generation of the burst errors, the "Gilbert–Elliott" (GE) channel model was used.
- The mean error probability here is also $p_{\rm M}=10^{-3}$.
- Contrast this with the very short "correlation period" $D_{\rm K}= 8$ with long-range statistical ties ⇒ $D_{\rm K}= 1000$.
First, we start again from the file "Stille.wav". We can see that a short error correlation duration of the GE model in the result is not too different from statistically independent errors, since each sample is represented with $16$ bits.
BSC model.
GE model with $D_{\rm K}= 8$.
GE model with $D_{\rm K}= 1000$.
The same channel parameters also apply to the following short piece of music and one recognizes similar characteristics.
BSC model.
GE model with $D_{\rm K}= 8$.
GE model with $D_{\rm K}= 1000$.
Note: All ( falsified ) BMP images and WAV audios for this chapter were generated with the Windows program "Digital Channel Models & Multimedia" from the (former) practical course "Simulation of Digital Transmission Systems" at the Chair of Communications Engineering of the TU Munich. The following links provide:
- the Windows program DKM ⇒ link refers to the ZIP version of the program; and
- the corresponding lab manual ⇒ link refers to the PDF version.
Exercises for the chapter
Exercise 5.8Z: Falsification of BMP Images