Difference between revisions of "Applets:Pulses and Spectra"
| (24 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLinkEnDe|pulsesAndSpectra_en|pulsesAndSpectra}} |
| − | + | ||
==Applet Description== | ==Applet Description== | ||
<br> | <br> | ||
| − | + | Time-limited symmetric signals ⇒ "pulses" $x(t)$ and the corresponding spectral functions $X(f)$ are considered, namely | |
| − | *Gaussian | + | |
| − | *rectangular | + | *Gaussian pulse, |
| − | *triangular | + | *rectangular pulse, |
| − | *trapezoidal | + | *triangular pulse, |
| − | *cosine | + | *trapezoidal pulse, |
| + | *raised cosine pulse, | ||
| + | *cosine square pulse. | ||
| + | |||
| + | Further it is to be noted: | ||
| + | * The functions $x(t)$ resp. $X(f)$ are shown for up to two parameter sets in one diagram each. | ||
| + | * The red curves and numbers apply to the left parameter set, the blue ones to the right parameter set. | ||
| + | * The abscissas $t$ (time) and $f$ (frequency) as well as the ordinates $x(t)$ (signal values) and $X(f)$ (spectral values) are normalized. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==Theoretical | + | ==Theoretical Background== |
<br> | <br> | ||
===Relationship $x(t)\Leftrightarrow X(f)$=== | ===Relationship $x(t)\Leftrightarrow X(f)$=== | ||
| − | * | + | *The relationship between the time function $x(t)$ and the spectrum $X(f)$ is given by the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|"first Fourier integral"]] : |
:$$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} | :$$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} | ||
| − | \rm FT\hspace{-0.1cm}: \ | + | \rm FT\hspace{-0.1cm}: \ Fourier \ transform.$$ |
| − | * | + | *In order to calculate the time function $x(f)$ from the spectral function $x(t)$ one needs the [[Signal_Representation/The_Fourier_Transform_and_its_Inverse#The_second_Fourier_integral|"second Fourier integral"]]: |
:$$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} | :$$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} | ||
| − | {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ | + | {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fourier \ transform.$$ |
| − | *In | + | *In all examples we use real and even functions. Thus: |
:$$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$ | :$$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$ | ||
| − | *$x(t)$ | + | *$x(t)$ and $X(f)$ have different units, for example $x(t)$ in $\rm V$, $X(f)$ in $\rm V/Hz$. |
| − | * | + | *The relationship between this module and the similarly constructed applet [[Applets:Frequenzgang_und_Impulsantwort|"Frequency response & Impulse response"]] is based on the [[Signal_Representation/The_Fourier_Transform_Theorems#Duality_Theorem|"Duality Theorem"]]. |
| − | * | + | *All times are normalized to a time $T$ and all frequencies are normalized to $1/T$ ⇒ the spectral values $X(f)$ still have to be multiplied by the normalization time $T$ . |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example:}$ If one sets a rectangular pulse with amplitude $A_1 = 1$ and equivalent pulse duration $\Delta t_1 = 1$ then $x_1(t)$ in the range $-0.5 < t < +0. 5$ equal to one and outside this range equal to zero. The spectral function $X_1(f)$ proceeds $\rm si$–shaped with $X_1(f= 0) = 1$ and the first zero at $f=1$. |
| − | * | + | *If a rectangular pulse with $A = K = 3 \ \rm V$ and $\delta t = T = 2 \ \rm ms$ is to be simulated with this setting, then all signal values with $K = 3 \ \rm V$ and all spectral values with $K \cdot T = 0. 006 \ \rm V/Hz$ to be multiplied by. |
| − | * | + | *The maximum spectral value is then $X(f= 0) = 0.006 \ \rm V/Hz$ and the first zero is at $f=1/T = 0.5 \ \rm kHz$.}} |
| − | ===Gaussian | + | ===Gaussian Pulse === |
| − | * | + | *The time function of the Gaussian pulse with height $K$ and (equivalent) duration $\Delta t$ is: |
:$$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$ | :$$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$ | ||
| − | * | + | *The equivalent time duration $\Delta t$ is obtained from the rectangle of equal area. |
| − | * | + | *The value at $t = \Delta t/2$ is smaller than the value at $t=0$ by the factor $0.456$ . |
| − | * | + | *For the spectral function we get according to the Fourier transform: |
:$$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$ | :$$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$ | ||
| − | * | + | *The smaller the equivalent time duration $\Delta t$ is, the wider and lower the spectrum ⇒ [[Signal_Representation/The_Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|"Reciprocity law of bandwidth and pulse duration"]]. |
| − | * | + | *Both $x(t)$ and $X(f)$ are not exactly zero at any $f$– or $t$–value, respectively. |
| − | * | + | *For practical applications, however, the Gaussian pulse can be assumed to be limited in time and frequency. For example, $x(t)$ has already dropped to less than $0.1\% $ of the maximum at $t=1.5 \delta t$ . |
| − | ===Rectangular | + | ===Rectangular Pulse === |
| − | * | + | *The time function of the rectangular pulse with height $K$ and (equivalent) duration $\Delta t$ is: |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{ | + | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$ |
| − | * | + | *The $\pm \Delta t/2$ value lies midway between the left- and right-hand limits. |
| − | * | + | *For the spectral function one obtains according to the laws of the Fourier transform (1st Fourier integral): |
| − | :$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{ | + | :$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{with} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$ |
| − | * | + | *The spectral value at $f=0$ is equal to the rectangular area of the time function. |
| − | * | + | *The spectral function has zeros at equidistant distances $1/\delta t$. |
| − | * | + | *The integral over the spectral function $X(f)$ is equal to the signal value at time $t=0$, i.e. the pulse height $K$. |
| − | ===Triangular | + | ===Triangular Pulse=== |
| − | * | + | *The time function of the triangular pulse with height $K$ and (equivalent) duration $\Delta t$ is: |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{ | + | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$ |
| − | * | + | *The absolute time duration is $2 \cdot \Delta t$; this is twice as large as that of the rectangle. |
| − | * | + | *For the spectral function, we obtain according to the Fourier transform: |
| − | :$$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{ | + | :$$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{with} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$ |
| − | * | + | *The above time function is equal to the convolution of two rectangular pulses, each with width $\delta t$. |
| − | * | + | *From this follows: $X(f)$ contains instead of the ${\rm si}$-function the ${\rm si}^2$-function. |
| − | *$X(f)$ | + | *$X(f)$ thus also has zeros at equidistant intervals $1/\rm f$ . |
| − | * | + | *The asymptotic decay of $X(f)$ occurs here with $1/f^2$, while for comparison the rectangular pulse decays with $1/f$ . |
| − | ===Trapezoidal | + | ===Trapezoidal Pulse === |
| − | + | The time function of the trapezoidal pulse with height $K$ and time parameters $t_1$ and $t_2$ is: | |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{ | + | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}}\quad \\ {\rm{for}}\quad \\ {\rm{for}} \quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$ |
| − | * | + | *For the equivalent pulse duration (rectangle of equal area) holds: $\Delta t = t_1+t_2$. |
| − | * | + | *The rolloff factor (in the time domain) characterizes the slope: |
:$$r=\frac{t_2-t_1}{t_2+t_1}.$$ | :$$r=\frac{t_2-t_1}{t_2+t_1}.$$ | ||
| − | * | + | *The special case $r=0$ corresponds to the rectangular pulse and the special case $r=1$ to the triangular pulse. |
| − | * | + | *For the spectral function one obtains according to the Fourier transform: |
| − | :$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{ | + | :$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{with} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$ |
| − | * | + | *The asymptotic decay of $X(f)$ lies between $1/f$ $($for rectangle, $r=0)$ and $1/f^2$ $($for triangle, $r=1)$. |
| − | === | + | ===Raised cosine Pulse === |
| − | + | The time function of the raised cosine pulse with height $K$ and time parameters $t_1$ and $t_2$ is: | |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{ | + | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}}\quad \\ {\rm{for}}\quad \\ {\rm{for}}\quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$ |
| − | * | + | *For the equivalent pulse duration (rectangle of equal area) holds: $\Delta t = t_1+t_2$. |
| − | * | + | *The rolloff factor (in the time domain) characterizes the slope: |
:$$r=\frac{t_2-t_1}{t_2+t_1}.$$ | :$$r=\frac{t_2-t_1}{t_2+t_1}.$$ | ||
| − | * | + | *The special case $r=0$ corresponds to the square pulse and the special case $r=1$ to the cosine square pulse. |
| − | * | + | *For the spectral function one obtains according to the Fourier transform: |
:$$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$ | :$$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$ | ||
| − | * | + | *The larger the rolloff factor $r$ is, the faster $X(f)$ decreases asymptotically with $f$ . |
| − | === | + | ===Cosine square Pulse === |
| − | * | + | *This is a special case of the raised cosine pulse and results for $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, \ t_2= \Delta t$: |
| − | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{ | + | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$ |
| − | * | + | *For the spectral function, we obtain according to the Fourier transform: |
:$$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$ | :$$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$ | ||
| − | * | + | *Because of the last ${\rm si}$-function is $X(f)=0$ for all multiples of $F=1/\delta t$. The equidistant zero crossings of the raised cosine pulse are preserved. |
| − | * | + | *Because of the bracket expression, $X(f)$ now exhibits further zero crossings at $f=\pm1.5 F$, $\pm2.5 F$, $\pm3.5 F$, ... . |
| − | * | + | *For frequency $f=\pm F/2$ the spectral values $K\cdot \Delta t/2$ are obtained. |
| − | * | + | *The asymptotic decay of $X(f)$ runs in this special case with $1/f^3$. |
==Exercises== | ==Exercises== | ||
| Line 133: | Line 136: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' Compare the <b>red Gaussian | + | '''(1)''' Compare the <b>red Gaussian pulse</b> $(A_1 = 1, \Delta t_1 = 1)$ with the <b>blue rectangular pulse</b> $(A_2 = 1, \Delta t_2 = 1)$ ⇒ default setting. |
<br> What are the differences in the time and frequency domain?}} | <br> What are the differences in the time and frequency domain?}} | ||
| − | * The Gaussian | + | * The Gaussian pulse theoretically reaches infinity in the time as well as in the frequency domain. <br> |
* Practically $x_1(t)$ for $|t| > 1.5$ and $X_1(f)$ for $|f| > 1.5$ are almost zero.<br> | * Practically $x_1(t)$ for $|t| > 1.5$ and $X_1(f)$ for $|f| > 1.5$ are almost zero.<br> | ||
* The rectangle is strictly limited in time: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ has shares in a much larger range than $X_1(f)$. <br> | * The rectangle is strictly limited in time: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ has shares in a much larger range than $X_1(f)$. <br> | ||
| − | * It holds $X_1(f = 0) = X_2(f = 0)$ since the integral over the Gaussian | + | * It holds $X_1(f = 0) = X_2(f = 0)$ since the integral over the Gaussian pulse $x_1(t)$ is equal to the integral over the rectangular pulse $x_2(t)$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(2)''' Compare the <b>red Gaussian | + | '''(2)''' Compare the <b>red Gaussian pulse</b> $(A_1 = 1, \Delta t_1 = 1)$ with the <b>blue rectangular pulse</b> $(A_2 = 1, \Delta t_2)$.<br> Vary the equivalent pulse duration $\Delta t_2$ between $0.5$ and $2$. Interpret the displayed graphs.}} |
| − | * One can recognize the reciprocity law of bandwidth and | + | * One can recognize the reciprocity law of bandwidth and pulse duration. The greater $\Delta t_2$, the higher and narrower the spectral function $X_2(f)$.<br> |
* For each setting of $\Delta t_2$, $x_1(t=0)$ and $x_2(t=0)$ are equal ⇒ Also, the integrals over $X_1(f)$ and $X_2(f)$ are identical. | * For each setting of $\Delta t_2$, $x_1(t=0)$ and $x_2(t=0)$ are equal ⇒ Also, the integrals over $X_1(f)$ and $X_2(f)$ are identical. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(3)''' Compare the <b>red Gaussian | + | '''(3)''' Compare the <b>red Gaussian pulse</b> $(A_1 = 1, \Delta t_1 = 1)$ with the <b>blue rectangular pulse</b> $(A_2 = 1, \Delta t_2 = 0.5)$.<br> Vary $\Delta t_2$ between $0.05$ and $2$. Interpret the displayed graphs and extrapolate the result.}} |
* The blue spectrum is now twice as wide as the red one, but only half as high. First zero of $X_1(f)$ at $f = 1$, of $X_2(f)$ at $f = 2$.<br> | * The blue spectrum is now twice as wide as the red one, but only half as high. First zero of $X_1(f)$ at $f = 1$, of $X_2(f)$ at $f = 2$.<br> | ||
| Line 160: | Line 163: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(4)''' Compare the <b> rectangular | + | '''(4)''' Compare the <b> rectangular pulse</b> $(A_1 = 1, \Delta t_1 = 1)$ with the <b>triangular pulse</b> $(A_2 = 1, \Delta t_2 = 1)$. Interpret the spectral functions.}} |
| − | * The (normalized) spectrum of the rectangle $x_1(t)$ with the (normalized) parameters $A_1 = 1, \ \ \Delta t_1 = 1$ is: $X_1(f)= {\rm si}(\pi\cdot f)$.<br> | + | * The (normalized) spectrum of the rectangle $x_1(t)$ with the (normalized) parameters $A_1 = 1, \ \ \Delta t_1 = 1$ is: $X_1(f)= {\rm si}(\pi\cdot f)= {\rm sinc}(f)$.<br> |
* The convolution of the rectangle $x_1(t)$ with itself gives the triangle $x_2(t) = x_1(t) \star x_1(t)$. By the convolution theorem: $X_2(f) = X_1(f)^2 $. <br> | * The convolution of the rectangle $x_1(t)$ with itself gives the triangle $x_2(t) = x_1(t) \star x_1(t)$. By the convolution theorem: $X_2(f) = X_1(f)^2 $. <br> | ||
| − | * By squaring the $\rm | + | * By squaring the ${\rm sinc}(f)$–shaped spectral function $X_1(f)$ the zeros of $X_2(f)$ remain unchanged. But now it holds that: $X_2(f) \ge 0$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(5)''' Compare the <b>trapezoidal | + | '''(5)''' Compare the <b>trapezoidal pulse</b> $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ with the |
| − | <b>triangular | + | <b>triangular pulse</b> $(A_2 = 1, \Delta t_2 = 1)$.<br> Vary $r_1$ between $0$ and $1$. Interpret the spectral function $X_1(f)$.}} |
| − | * The trapezoidal | + | * The trapezoidal pulse with roll–off factor $r_1= 0$ is identical to the rectangular pulse. The "normalized spectrum" is $X_1(f)= {\rm sinc}(f)$.<br> |
| − | * The trapezoidal | + | * The trapezoidal pulse with roll–off factor $r_1= 1$ is identical to the triangular pulse. The "normalized spectrum" is $X_1(f)= {\rm sinc}^2(f)$. <br> |
* In both cases $X_1(f)$ has equidistant zeros at $\pm 1$, $\pm 2$, ... (none else); $0 < r_1 < 1$: depending on $r_1$ further zeros. | * In both cases $X_1(f)$ has equidistant zeros at $\pm 1$, $\pm 2$, ... (none else); $0 < r_1 < 1$: depending on $r_1$ further zeros. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(6)''' Compare this <b>trapezoidal | + | '''(6)''' Compare this <b>trapezoidal pulse</b> with the <b>cosine roll-off pulse</b> |
$(A_2 = 1,\ \Delta t_2 = 1.0,\ r_2 = 0.5)$.<br> Vary $r_2$ between $0$ and $1$. Interpret the spectral function $X_2(f)$ for $r_2 = 0.7$.}} | $(A_2 = 1,\ \Delta t_2 = 1.0,\ r_2 = 0.5)$.<br> Vary $r_2$ between $0$ and $1$. Interpret the spectral function $X_2(f)$ for $r_2 = 0.7$.}} | ||
| − | * With the same $r= 0.5$ the cosine- | + | * With the same $r= 0.5$ the cosine roll-off pulse $X_2(f)$ is for $f > 1$ greater in magnitude than the trapezoidal pulse.<br> |
| − | * With the same | + | * With the same roll-off factor $(r_1 = r_2= 0.5)$ the drop of $X_2(f)$ around the frequency $f = 0.5$ is steeper than the drop of $X_1(f)$. <br> |
* With $r_1 = 0.5$ and $r_2 = 0.7$ $x_1(t) \approx x_2(t)$ is valid and therefore also $X_1(f) \approx X_2(f)$. Comparable edge steepness. | * With $r_1 = 0.5$ and $r_2 = 0.7$ $x_1(t) \approx x_2(t)$ is valid and therefore also $X_1(f) \approx X_2(f)$. Comparable edge steepness. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(7)''' Compare the <b>red trapezoidal | + | '''(7)''' Compare the <b>red trapezoidal pulse</b> $(A_1 = 1, \Delta t_1 = 1, \ r_1 = 1)$ with the <b>blue cosine roll-off pulse</b> $(A_2 = 1,\ \Delta t_2 = 1.0, \ r_2 = 1)$.<br> Interpret the time function $x_2(t)$ and the spectral function $X_2(f)$ system theoretically.}} |
| − | * $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \ \text{for} \ |t| \le 1$ is the cosine | + | * $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \ \text{for} \ |t| \le 1$ is the cosine square pulse. Zeros at $f = \pm 1$, $\pm 2$, ... <br> |
* For the frequency $f=\pm 0.5$ one obtains the spectral values $X_2(f)=0.5$. The asymptotic decline is shown here with $1/f^3$. | * For the frequency $f=\pm 0.5$ one obtains the spectral values $X_2(f)=0.5$. The asymptotic decline is shown here with $1/f^3$. | ||
| Line 194: | Line 197: | ||
==Applet Manual== | ==Applet Manual== | ||
| − | + | ||
| − | [[File: | + | [[File:EN_Impulse_Man_neu.png|right|frame|Screenshot]] |
| + | |||
| + | |||
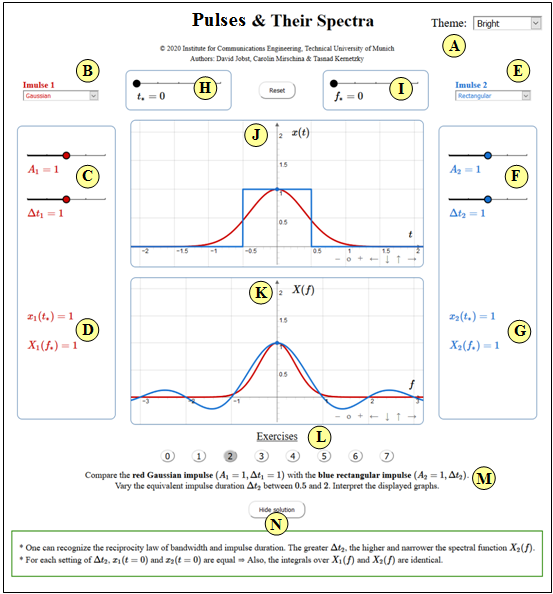
'''(A)''' Theme (changeable graphical user interface design) | '''(A)''' Theme (changeable graphical user interface design) | ||
:* Dark: dark background (recommended by the authors) | :* Dark: dark background (recommended by the authors) | ||
| Line 202: | Line 207: | ||
:* Protanopia: for users with pronounced red visual impairment | :* Protanopia: for users with pronounced red visual impairment | ||
| − | '''(B)''' Preselection for pulse shape $x_1(t)$ | + | '''(B)''' Preselection for pulse shape $x_1(t)$ ⇒ red curve |
'''(C)''' Parameter definition for $x_1(t)$ | '''(C)''' Parameter definition for $x_1(t)$ | ||
| Line 208: | Line 213: | ||
'''(D)''' Numeric output for $x_1(t_*)$ and $X_1(f_*)$ | '''(D)''' Numeric output for $x_1(t_*)$ and $X_1(f_*)$ | ||
| − | '''(E)''' Preselection for pulse shape $x_2(t)$ | + | '''(E)''' Preselection for pulse shape $x_2(t)$ ⇒ blue curve |
'''(F)''' Parameter definition for $x_2(t)$ | '''(F)''' Parameter definition for $x_2(t)$ | ||
| Line 227: | Line 232: | ||
'''(N)''' Show and hide sample solution | '''(N)''' Show and hide sample solution | ||
| + | <br clear=all> | ||
| − | + | ==About the Authors== | |
| − | ==About the | ||
<br> | <br> | ||
| + | This interactive calculation tool was designed and implemented at the [https://www.ei.tum.de/en/lnt/home/ Institute for Communications Engineering] at the [https://www.tum.de/en Technical University of Munich]. | ||
| + | *The first version was created in 2005 by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Ji_Li_.28Bachelorarbeit_EI_2003.2C_Diplomarbeit_EI_2005.29|Ji Li]] as part of her diploma thesis with “FlashMX – Actionscript” (Supervisor: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). | ||
| + | *In 2017 the program was redesigned by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#David_Jobst_.28Ingenieurspraxis_Math_2017.29|David Jobst]] (Ingenieurspraxis_Math, Supervisor: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]] ) via "HTML5". | ||
| + | *Last revision and English version 2020 by [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] in the context of a working student activity. | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Once again: Open Applet in new Tab== | ==Once again: Open Applet in new Tab== | ||
| − | {{ | + | {{LntAppletLinkEnDe|pulsesAndSpectra_en|pulsesAndSpectra}} |
| − | |||
<br><br> | <br><br> | ||
Latest revision as of 13:10, 21 April 2023
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Description
Time-limited symmetric signals ⇒ "pulses" $x(t)$ and the corresponding spectral functions $X(f)$ are considered, namely
- Gaussian pulse,
- rectangular pulse,
- triangular pulse,
- trapezoidal pulse,
- raised cosine pulse,
- cosine square pulse.
Further it is to be noted:
- The functions $x(t)$ resp. $X(f)$ are shown for up to two parameter sets in one diagram each.
- The red curves and numbers apply to the left parameter set, the blue ones to the right parameter set.
- The abscissas $t$ (time) and $f$ (frequency) as well as the ordinates $x(t)$ (signal values) and $X(f)$ (spectral values) are normalized.
Theoretical Background
Relationship $x(t)\Leftrightarrow X(f)$
- The relationship between the time function $x(t)$ and the spectrum $X(f)$ is given by the "first Fourier integral" :
- $$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fourier \ transform.$$
- In order to calculate the time function $x(f)$ from the spectral function $x(t)$ one needs the "second Fourier integral":
- $$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fourier \ transform.$$
- In all examples we use real and even functions. Thus:
- $$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$
- $x(t)$ and $X(f)$ have different units, for example $x(t)$ in $\rm V$, $X(f)$ in $\rm V/Hz$.
- The relationship between this module and the similarly constructed applet "Frequency response & Impulse response" is based on the "Duality Theorem".
- All times are normalized to a time $T$ and all frequencies are normalized to $1/T$ ⇒ the spectral values $X(f)$ still have to be multiplied by the normalization time $T$ .
$\text{Example:}$ If one sets a rectangular pulse with amplitude $A_1 = 1$ and equivalent pulse duration $\Delta t_1 = 1$ then $x_1(t)$ in the range $-0.5 < t < +0. 5$ equal to one and outside this range equal to zero. The spectral function $X_1(f)$ proceeds $\rm si$–shaped with $X_1(f= 0) = 1$ and the first zero at $f=1$.
- If a rectangular pulse with $A = K = 3 \ \rm V$ and $\delta t = T = 2 \ \rm ms$ is to be simulated with this setting, then all signal values with $K = 3 \ \rm V$ and all spectral values with $K \cdot T = 0. 006 \ \rm V/Hz$ to be multiplied by.
- The maximum spectral value is then $X(f= 0) = 0.006 \ \rm V/Hz$ and the first zero is at $f=1/T = 0.5 \ \rm kHz$.
Gaussian Pulse
- The time function of the Gaussian pulse with height $K$ and (equivalent) duration $\Delta t$ is:
- $$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$
- The equivalent time duration $\Delta t$ is obtained from the rectangle of equal area.
- The value at $t = \Delta t/2$ is smaller than the value at $t=0$ by the factor $0.456$ .
- For the spectral function we get according to the Fourier transform:
- $$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$
- The smaller the equivalent time duration $\Delta t$ is, the wider and lower the spectrum ⇒ "Reciprocity law of bandwidth and pulse duration".
- Both $x(t)$ and $X(f)$ are not exactly zero at any $f$– or $t$–value, respectively.
- For practical applications, however, the Gaussian pulse can be assumed to be limited in time and frequency. For example, $x(t)$ has already dropped to less than $0.1\% $ of the maximum at $t=1.5 \delta t$ .
Rectangular Pulse
- The time function of the rectangular pulse with height $K$ and (equivalent) duration $\Delta t$ is:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$
- The $\pm \Delta t/2$ value lies midway between the left- and right-hand limits.
- For the spectral function one obtains according to the laws of the Fourier transform (1st Fourier integral):
- $$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{with} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$
- The spectral value at $f=0$ is equal to the rectangular area of the time function.
- The spectral function has zeros at equidistant distances $1/\delta t$.
- The integral over the spectral function $X(f)$ is equal to the signal value at time $t=0$, i.e. the pulse height $K$.
Triangular Pulse
- The time function of the triangular pulse with height $K$ and (equivalent) duration $\Delta t$ is:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$
- The absolute time duration is $2 \cdot \Delta t$; this is twice as large as that of the rectangle.
- For the spectral function, we obtain according to the Fourier transform:
- $$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{with} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$
- The above time function is equal to the convolution of two rectangular pulses, each with width $\delta t$.
- From this follows: $X(f)$ contains instead of the ${\rm si}$-function the ${\rm si}^2$-function.
- $X(f)$ thus also has zeros at equidistant intervals $1/\rm f$ .
- The asymptotic decay of $X(f)$ occurs here with $1/f^2$, while for comparison the rectangular pulse decays with $1/f$ .
Trapezoidal Pulse
The time function of the trapezoidal pulse with height $K$ and time parameters $t_1$ and $t_2$ is:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}}\quad \\ {\rm{for}}\quad \\ {\rm{for}} \quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$
- For the equivalent pulse duration (rectangle of equal area) holds: $\Delta t = t_1+t_2$.
- The rolloff factor (in the time domain) characterizes the slope:
- $$r=\frac{t_2-t_1}{t_2+t_1}.$$
- The special case $r=0$ corresponds to the rectangular pulse and the special case $r=1$ to the triangular pulse.
- For the spectral function one obtains according to the Fourier transform:
- $$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{with} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$
- The asymptotic decay of $X(f)$ lies between $1/f$ $($for rectangle, $r=0)$ and $1/f^2$ $($for triangle, $r=1)$.
Raised cosine Pulse
The time function of the raised cosine pulse with height $K$ and time parameters $t_1$ and $t_2$ is:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}}\quad \\ {\rm{for}}\quad \\ {\rm{for}}\quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$
- For the equivalent pulse duration (rectangle of equal area) holds: $\Delta t = t_1+t_2$.
- The rolloff factor (in the time domain) characterizes the slope:
- $$r=\frac{t_2-t_1}{t_2+t_1}.$$
- The special case $r=0$ corresponds to the square pulse and the special case $r=1$ to the cosine square pulse.
- For the spectral function one obtains according to the Fourier transform:
- $$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$
- The larger the rolloff factor $r$ is, the faster $X(f)$ decreases asymptotically with $f$ .
Cosine square Pulse
- This is a special case of the raised cosine pulse and results for $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, \ t_2= \Delta t$:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$
- For the spectral function, we obtain according to the Fourier transform:
- $$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$
- Because of the last ${\rm si}$-function is $X(f)=0$ for all multiples of $F=1/\delta t$. The equidistant zero crossings of the raised cosine pulse are preserved.
- Because of the bracket expression, $X(f)$ now exhibits further zero crossings at $f=\pm1.5 F$, $\pm2.5 F$, $\pm3.5 F$, ... .
- For frequency $f=\pm F/2$ the spectral values $K\cdot \Delta t/2$ are obtained.
- The asymptotic decay of $X(f)$ runs in this special case with $1/f^3$.
Exercises
- First select the number $(1,\text{...}, 7)$ of the exercise. The number $0$ corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show solution".
- "Red" refers to the first parameter set ⇒ $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$, "Blue" refers to the second parameter set ⇒ $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.
- Values with magnitude less than $0.0005$ are output in the program as "zero".
(1) Compare the red Gaussian pulse $(A_1 = 1, \Delta t_1 = 1)$ with the blue rectangular pulse $(A_2 = 1, \Delta t_2 = 1)$ ⇒ default setting.
What are the differences in the time and frequency domain?
- The Gaussian pulse theoretically reaches infinity in the time as well as in the frequency domain.
- Practically $x_1(t)$ for $|t| > 1.5$ and $X_1(f)$ for $|f| > 1.5$ are almost zero.
- The rectangle is strictly limited in time: $x_2(|t| > 0.5) \equiv 0$. $X_2(f)$ has shares in a much larger range than $X_1(f)$.
- It holds $X_1(f = 0) = X_2(f = 0)$ since the integral over the Gaussian pulse $x_1(t)$ is equal to the integral over the rectangular pulse $x_2(t)$.
(2) Compare the red Gaussian pulse $(A_1 = 1, \Delta t_1 = 1)$ with the blue rectangular pulse $(A_2 = 1, \Delta t_2)$.
Vary the equivalent pulse duration $\Delta t_2$ between $0.5$ and $2$. Interpret the displayed graphs.
- One can recognize the reciprocity law of bandwidth and pulse duration. The greater $\Delta t_2$, the higher and narrower the spectral function $X_2(f)$.
- For each setting of $\Delta t_2$, $x_1(t=0)$ and $x_2(t=0)$ are equal ⇒ Also, the integrals over $X_1(f)$ and $X_2(f)$ are identical.
(3) Compare the red Gaussian pulse $(A_1 = 1, \Delta t_1 = 1)$ with the blue rectangular pulse $(A_2 = 1, \Delta t_2 = 0.5)$.
Vary $\Delta t_2$ between $0.05$ and $2$. Interpret the displayed graphs and extrapolate the result.
- The blue spectrum is now twice as wide as the red one, but only half as high. First zero of $X_1(f)$ at $f = 1$, of $X_2(f)$ at $f = 2$.
- Reduction of $\Delta t_2$: $X_2(f)$ lower and wider. Very flat course at $\Delta t_2 = 0.05$: $X_2(f = 0)= 0.05$, $X_2(f = \pm 3)= 0.048$.
- If one choose $\Delta t_2 = \varepsilon \to 0$ (not possible in the program), the result would be the almost constant, very small spectrum $X_2(f)=A \cdot \varepsilon \to 0$.
- Increasing the amplitude to $A=1/\varepsilon$ results in the constant spectral function $X_2(f) = 1$ of the Dirac function $\delta(t)$. That means:
- $\delta(t)$ is approximated by a rectangle $($width $\Delta t = \varepsilon \to 0$, height $A = 1/\varepsilon \to \infty)$. The weight of the Dirac function is one: $x(t) = 1 \cdot \delta (t)$.
(4) Compare the rectangular pulse $(A_1 = 1, \Delta t_1 = 1)$ with the triangular pulse $(A_2 = 1, \Delta t_2 = 1)$. Interpret the spectral functions.
- The (normalized) spectrum of the rectangle $x_1(t)$ with the (normalized) parameters $A_1 = 1, \ \ \Delta t_1 = 1$ is: $X_1(f)= {\rm si}(\pi\cdot f)= {\rm sinc}(f)$.
- The convolution of the rectangle $x_1(t)$ with itself gives the triangle $x_2(t) = x_1(t) \star x_1(t)$. By the convolution theorem: $X_2(f) = X_1(f)^2 $.
- By squaring the ${\rm sinc}(f)$–shaped spectral function $X_1(f)$ the zeros of $X_2(f)$ remain unchanged. But now it holds that: $X_2(f) \ge 0$.
(5) Compare the trapezoidal pulse $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$ with the
triangular pulse $(A_2 = 1, \Delta t_2 = 1)$.
Vary $r_1$ between $0$ and $1$. Interpret the spectral function $X_1(f)$.
- The trapezoidal pulse with roll–off factor $r_1= 0$ is identical to the rectangular pulse. The "normalized spectrum" is $X_1(f)= {\rm sinc}(f)$.
- The trapezoidal pulse with roll–off factor $r_1= 1$ is identical to the triangular pulse. The "normalized spectrum" is $X_1(f)= {\rm sinc}^2(f)$.
- In both cases $X_1(f)$ has equidistant zeros at $\pm 1$, $\pm 2$, ... (none else); $0 < r_1 < 1$: depending on $r_1$ further zeros.
(6) Compare this trapezoidal pulse with the cosine roll-off pulse
$(A_2 = 1,\ \Delta t_2 = 1.0,\ r_2 = 0.5)$.
Vary $r_2$ between $0$ and $1$. Interpret the spectral function $X_2(f)$ for $r_2 = 0.7$.
- With the same $r= 0.5$ the cosine roll-off pulse $X_2(f)$ is for $f > 1$ greater in magnitude than the trapezoidal pulse.
- With the same roll-off factor $(r_1 = r_2= 0.5)$ the drop of $X_2(f)$ around the frequency $f = 0.5$ is steeper than the drop of $X_1(f)$.
- With $r_1 = 0.5$ and $r_2 = 0.7$ $x_1(t) \approx x_2(t)$ is valid and therefore also $X_1(f) \approx X_2(f)$. Comparable edge steepness.
(7) Compare the red trapezoidal pulse $(A_1 = 1, \Delta t_1 = 1, \ r_1 = 1)$ with the blue cosine roll-off pulse $(A_2 = 1,\ \Delta t_2 = 1.0, \ r_2 = 1)$.
Interpret the time function $x_2(t)$ and the spectral function $X_2(f)$ system theoretically.
- $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \ \text{for} \ |t| \le 1$ is the cosine square pulse. Zeros at $f = \pm 1$, $\pm 2$, ...
- For the frequency $f=\pm 0.5$ one obtains the spectral values $X_2(f)=0.5$. The asymptotic decline is shown here with $1/f^3$.
Applet Manual
(A) Theme (changeable graphical user interface design)
- Dark: dark background (recommended by the authors)
- Bright: white background (recommended for beamers and printouts)
- Deuteranopia: for users with pronounced green visual impairment
- Protanopia: for users with pronounced red visual impairment
(B) Preselection for pulse shape $x_1(t)$ ⇒ red curve
(C) Parameter definition for $x_1(t)$
(D) Numeric output for $x_1(t_*)$ and $X_1(f_*)$
(E) Preselection for pulse shape $x_2(t)$ ⇒ blue curve
(F) Parameter definition for $x_2(t)$
(G) Numeric output for $x_2(t_*)$ and $X_2(f_*)$
(H) Setting the time $t_*$ for the numeric output
(I) Setting the frequency $f_*$ for the numeric output
(J) Graphic field for the time domain
(K) Graphic field for the frequency domain
(L) Selection of the exercise according to the numbers
(M) Task description and questions
(N) Show and hide sample solution
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first version was created in 2005 by Ji Li as part of her diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- In 2017 the program was redesigned by David Jobst (Ingenieurspraxis_Math, Supervisor: Tasnád Kernetzky ) via "HTML5".
- Last revision and English version 2020 by Carolin Mirschina in the context of a working student activity.