Difference between revisions of "Signal Representation/Special Cases of Pulses"
| (50 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Aperiodic Signals - Impulses |
| − | |Vorherige Seite= | + | |Vorherige Seite=The Fourier Transform and its Inverse |
| − | |Nächste Seite= | + | |Nächste Seite=Fourier Transform Theorems |
}} | }} | ||
| − | == | + | ==Rectangular pulse== |
| + | <br> | ||
| + | [[File:Sig_T_3_2_S1_version3.png|right|frame|Rectangular pulse and its spectrum]] | ||
| + | One speaks of a »'''rectangular pulse'''«, if the following applies for the time domain: | ||
| − | + | :$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}A \\ A /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$ | |
| − | + | ||
| + | $A$ denotes the amplitude of the pulse and $T$ the pulse duration. | ||
| − | $$ | + | The corresponding spectral function $X(f)$ is obtained by using the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|»first Fourier integral«]]: |
| − | + | :$$X(f) = \int_{ - T/2}^{+T/2} A \cdot {\rm e}^{ -{\rm j}2\pi ft}\, {\rm d}t ,$$ | |
| − | + | :$$\Rightarrow \hspace{0.3cm} X(f) = A \cdot \int_{ - T/2}^{+T/2} {\cos ( {2\pi}ft )\,{\rm d}t - {\rm j} \cdot A} \int_{ - T/2}^{+T/2} {\sin ( {2\pi ft} )}\,{\rm d}t .$$ | |
| + | *Here the integration limits $\pm T/2$ take into account that $x(t)$ is identical to zero outside the interval from $-T/2$ to $+T/2$. | ||
| − | + | *The second integral disappears due to the odd integrand and you get | |
| − | $$X(f) = \ | + | :$$X(f) = \frac{A \cdot \sin \left( {\pi fT} \right)}{\pi f}.$$ |
| − | + | *By extending the numerator and denominator each with $T$ one can also write for the spectral function of the rectangular pulse: | |
| − | $$X(f) = \ | + | :$$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right)\hspace{1.3cm}\text{resp.}\hspace{1.3cm}\ X( f ) = A \cdot T \cdot {\rm sinc}\hspace{-0.08cm}\left( {fT} \right).$$ |
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definitions:}$ For abbreviation we define the following functions: | ||
| + | *»'''sinc–function«''' $($predominantly used in Anglo-American literature$)$ | ||
| + | :$${\rm sinc}( x ) = {\sin (\pi x) }/(\pi x ),$$ | ||
| − | + | *»'''si–function'''« or »$\text{splitting function}$« $($predominantly used in German literature$)$ | |
| − | + | :$${\rm si}\left( x \right) = \sin \left( x \right)/x = {\rm sinc}(x/\pi ).$$}} | |
| − | |||
| − | |||
| − | |||
| + | <u>Note:</u> In our $\rm LNTwww$ (because of the German original) we mostly use the function ${\rm si}(x)$, but important results are also given in the ${\rm sinc}(x)$ form. | ||
| − | + | ⇒ As the right graph on the top shows, $X(f)$ has the following properties: | |
| − | + | *The maximum is at frequency $f=0$ and has the value $A \cdot T$ ⇒ »area of the rectangle«. | |
| − | $ | ||
| − | + | *For the frequencies $f_n = n/T$ with $n = ±1, ±2, ±3,\text{ ...} $ the spectral function has zeroes: | |
| − | * | ||
| − | |||
| − | : $X( {f = f_n } ) = 0.$ | + | :$$X( {f = f_n } ) = 0.$$ |
| − | * | + | *The following constraint applies to the magnitude spectrum: |
| − | $$\left| {X( f )} \right| \le \frac{A}{\pi \cdot \left| f \right|}.$$ | + | :$$\left| {X( f )} \right| \le \frac{A}{\pi \cdot \left| f \right|}.$$ |
| − | == | + | ==Gaussian pulse== |
| − | + | <br> | |
| − | + | Another example of an aperiodic signal is the »'''Gaussian pulse'''«: | |
| − | $$x(t) = A \cdot {\rm e}^{ - \pi \left( {t/\Delta t} \right)^2 } .$$ | + | :$$x(t) = A \cdot {\rm e}^{ - \pi \left( {t/\Delta t} \right)^2 } .$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| + | This pulse is described by two parameters, namely | ||
| + | *the pulse amplitude $A$, and | ||
| + | *the equivalent pulse duration $\Delta t$. | ||
| − | |||
| − | |||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ The term »'''equivalent pulse duration'''« is generally used to describe the duration of a rectangular pulse with the same amplitude and area as the given pulse-like signal $x(t)$: | ||
| − | {{ | + | :$$\Delta t = \frac{1}{A }\cdot \hspace{-0.15cm} \int_{ - \infty }^{ + \infty } {x( t )\, {\rm d}t.}$$}} |
| − | + | The Gaussian pulse $x(t)$ has the following properties $($see graphic in $\text{Example 1})$: | |
| − | + | #The time function is for all times from $-\infty$ to $+\infty$ existent and positive. | |
| − | + | #This means simultaneously: The absolute pulse duration is infinite. | |
| − | + | #With the above definition the pulse maximum $A$ is at $t = 0$. | |
| − | + | #At $t = \pm \Delta t/2$ , the pulse is decayed to $\text{e}^{-\pi/4} \approx 0.456$ of the maximum. And at $t = \pm \Delta t$, the signal value is less than $3.5 \cdot 10^{-6} \cdot A$. | |
| + | #The spectral function $X(f)$ is also Gaussian and has similar characteristics as the Gaussian pulse $x(t)$: | ||
| − | $$X(f) = A \cdot \Delta t \cdot {\rm e}^{ - \pi \left( {f \cdot \Delta t} \right)^2 }.$$ | + | ::$$X(f) = A \cdot \Delta t \cdot {\rm e}^{ - \pi \left( {f \hspace{0.05cm} \cdot \hspace{0.05cm} \Delta t} \right)^2 }.$$ |
| − | + | In the section [[Signal_Representation/Fourier_Transform_Theorems#Reciprocity_Theorem_of_time_duration_and_bandwidth|»Reciprocity Theorem«]] the analogies of time domain and frequency domain of the Gaussian pulse are discussed in detail. | |
| − | |||
| − | |||
| + | The following example illustrates the similarities and differences between the Gaussian pulse $x(t)$ and its spectrum $X(f)$. | ||
| − | {{ | + | {{GraueBox|TEXT= |
| + | [[File:P_ID559__Sig_T_3_2_S2_b_neu.png|right|frame|Gaussian pulse and its spectrum $($with numerical values$)$]] | ||
| + | $\text{Example 1:}$ | ||
| + | The output power pulse $x(t)$ of a laser for digital optical transmission can be assumed to be Gaussian in the equivalent low-pass range with good approximation. | ||
| − | + | Let the signal parameters be $A = 1 \,\text{mW}$ and $\Delta t =1 \,\text{ns}$. | |
| − | |||
| − | + | This gives the following comparable parameters in the spectral range: | |
| − | + | * The maximum $X_0 = X(f=0) = A \cdot \Delta t = 10^{-12} \,\text{W/Hz}$, | |
| − | * | ||
| − | |||
| + | *the equivalent bandwidth $\Delta f = 1/\Delta t = 1 \,\text{GHz}$. | ||
| − | |||
| − | |||
| + | Theoretically, the absolute frequency band extends to infinity. However, at $f = 2 \cdot \Delta f = 2\,\text{GHz}$ the spectral function is already reduced by the factor $3.5 \cdot 10^{-6}$ compared to its maximum.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ⇒ We would like to draw your attention to two interactive applets on this topic with which you can display the time and frequency domain representations of the Gaussian pulse, rectangular pulse, triangular pulse, trapezoidal pulse and cosine rolloff pulse or the comparable quantities of an LTI system parameterized: | |
| + | *[[Applets:Pulses_and_Spectra|»Pulses and Spectra«]], | ||
| + | *[[Applets:Frequenzgang_und_Impulsantwort|»Frequency Response and Impulse Response«]]. | ||
| − | |||
| − | + | ==Dirac delta or impulse== | |
| + | <br> | ||
| + | In the chapter [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal#Dirac_.28delta.29_function_in_frequency_domain|»Periodic Signals«]] the »Dirac delta function« was already used to describe the spectrum of a direct current $\rm (DC)$ signal or a harmonic oscillation. However, in Communications Engineering it is also common and extremely advantageous to describe and analyze short-term processes with the help of this mathematical function in the time domain. | ||
| − | |||
| − | |||
| − | $$x(t) = X_0 \cdot \delta (t),$$ | + | {{BlaueBox|TEXT= |
| + | [[File:Sig_T_3_2_S3_version3.png|right|frame|Dirac delta and corresponding spectrum]] | ||
| + | $\text{Definition:}$ | ||
| + | A »'''Dirac delta'''«, also called»'''impulse'''«, is denoted as | ||
| + | :$$x(t) = X_0 \cdot \delta (t),$$ | ||
| − | + | and can be characterised as follows $($see plot$)$: | |
| − | + | *The Dirac delta is infinitely narrow ⇒ it holds $x(t)\equiv 0$ for $t \neq 0$ and at time $t = 0$ the Dirac delta is infinitely high. | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *If $x(t)$ describes a voltage curve, then the impulse weight $X_0$ has the unit "$\textrm{V} \cdot \textrm{s}$" $($i.e. the unit "$\textrm{V}/\textrm{Hz}$" of a spectral function$)$, since $\delta (t)$ itself has the unit "$1/\textrm{s}$". | |
| − | + | *The Fourier transform of the Dirac delta includes all frequencies $f$ equally: | |
| − | + | :$$X(f) = X_0 = \rm const.$$}} | |
| − | |||
| − | |||
| − | + | The properties mentioned here are shown in the $($German language$)$ learning video: <br> [[Herleitung_und_Visualisierung_der_Diracfunktion_(Lernvideo)|»Herleitung und Visualisierung der Diracfunktion«]] ⇒ "Derivation and visualisation of the Dirac delta function". | |
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Example 2:}$ We consider a network with low-pass characteristic and very low cutoff frequency $f_{\rm G} = 10\,\text{ kHz}$. The output signal $y(t)$ does not change significantly when one of the sketched signals $x_1(t)$, $x_2(t)$ or $x_3(t)$ is applied to the input. This result can be interpreted as follows: | |
| − | + | [[File:P_ID561__Sig_T_3_2_S3b_neu.png|right|frame|On the significance of the Dirac delta]] | |
| − | + | ||
| − | + | #The »equivalent pulse durations« are the same in each case $(\Delta t = 1\, µ\text{s})$ and this is much smaller than $1/f_{\rm G} = 100 \, µ\text{s}$. The actual pulse shape $($rectangle or triangle$)$ has only a minor influence on the output signal $y(t)$. | |
| − | + | #Both the rectangle $x_1(t)$ and the triangle $x_2(t)$ can be approximated by the Dirac delta $x_3(t)$. The impulse weight $X_0 = 6 \cdot 10^{-6}\, \text{Vs}$ must be equal to the pulse areas of $x_1(t)$ resp. $x_2(t)$. | |
| − | + | #However, a sufficiently small cutoff frequency is required for this approximation. This simplification would not be permitted with $f_{\rm G} = 10 \, \text{MHz}$ ⇒ $1/f_{\rm G} = 100 \, \text{ns}$. | |
| − | + | #Even if the Dirac delta is drawn with the same height as the other two pulses, it still has an infinite value at the time $t = 0$. | |
| − | + | #For the Dirac delta the impulse area $($»impulse weight«$)$ is always specified. This differs from the other pulse amplitudes already in the unit $($e.g. "Vs" instead of "V"$)$.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Exercises for the chapter== |
| − | [[Aufgaben:3.3 | + | [[Aufgaben:Exercise 3.3: From The Signal to the Spectrum|Exercise 3.3: From the Signal to the Spectrum]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_3.3Z:_Rectangular_Pulse_and_Dirac_Delta|Exercise 3.3Z: Rectangular Pulse and Dirac Delta]] |
{{Display}} | {{Display}} | ||
Latest revision as of 17:26, 15 November 2023
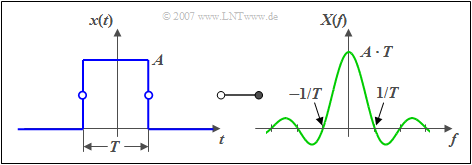
Rectangular pulse
One speaks of a »rectangular pulse«, if the following applies for the time domain:
- $$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}A \\ A /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$
$A$ denotes the amplitude of the pulse and $T$ the pulse duration.
The corresponding spectral function $X(f)$ is obtained by using the »first Fourier integral«:
- $$X(f) = \int_{ - T/2}^{+T/2} A \cdot {\rm e}^{ -{\rm j}2\pi ft}\, {\rm d}t ,$$
- $$\Rightarrow \hspace{0.3cm} X(f) = A \cdot \int_{ - T/2}^{+T/2} {\cos ( {2\pi}ft )\,{\rm d}t - {\rm j} \cdot A} \int_{ - T/2}^{+T/2} {\sin ( {2\pi ft} )}\,{\rm d}t .$$
- Here the integration limits $\pm T/2$ take into account that $x(t)$ is identical to zero outside the interval from $-T/2$ to $+T/2$.
- The second integral disappears due to the odd integrand and you get
- $$X(f) = \frac{A \cdot \sin \left( {\pi fT} \right)}{\pi f}.$$
- By extending the numerator and denominator each with $T$ one can also write for the spectral function of the rectangular pulse:
- $$X( f ) = A \cdot T \cdot {\rm si}\hspace{-0.08cm}\left( {\pi fT} \right)\hspace{1.3cm}\text{resp.}\hspace{1.3cm}\ X( f ) = A \cdot T \cdot {\rm sinc}\hspace{-0.08cm}\left( {fT} \right).$$
$\text{Definitions:}$ For abbreviation we define the following functions:
- »sinc–function« $($predominantly used in Anglo-American literature$)$
- $${\rm sinc}( x ) = {\sin (\pi x) }/(\pi x ),$$
- »si–function« or »$\text{splitting function}$« $($predominantly used in German literature$)$
- $${\rm si}\left( x \right) = \sin \left( x \right)/x = {\rm sinc}(x/\pi ).$$
Note: In our $\rm LNTwww$ (because of the German original) we mostly use the function ${\rm si}(x)$, but important results are also given in the ${\rm sinc}(x)$ form.
⇒ As the right graph on the top shows, $X(f)$ has the following properties:
- The maximum is at frequency $f=0$ and has the value $A \cdot T$ ⇒ »area of the rectangle«.
- For the frequencies $f_n = n/T$ with $n = ±1, ±2, ±3,\text{ ...} $ the spectral function has zeroes:
- $$X( {f = f_n } ) = 0.$$
- The following constraint applies to the magnitude spectrum:
- $$\left| {X( f )} \right| \le \frac{A}{\pi \cdot \left| f \right|}.$$
Gaussian pulse
Another example of an aperiodic signal is the »Gaussian pulse«:
- $$x(t) = A \cdot {\rm e}^{ - \pi \left( {t/\Delta t} \right)^2 } .$$
This pulse is described by two parameters, namely
- the pulse amplitude $A$, and
- the equivalent pulse duration $\Delta t$.
$\text{Definition:}$ The term »equivalent pulse duration« is generally used to describe the duration of a rectangular pulse with the same amplitude and area as the given pulse-like signal $x(t)$:
- $$\Delta t = \frac{1}{A }\cdot \hspace{-0.15cm} \int_{ - \infty }^{ + \infty } {x( t )\, {\rm d}t.}$$
The Gaussian pulse $x(t)$ has the following properties $($see graphic in $\text{Example 1})$:
- The time function is for all times from $-\infty$ to $+\infty$ existent and positive.
- This means simultaneously: The absolute pulse duration is infinite.
- With the above definition the pulse maximum $A$ is at $t = 0$.
- At $t = \pm \Delta t/2$ , the pulse is decayed to $\text{e}^{-\pi/4} \approx 0.456$ of the maximum. And at $t = \pm \Delta t$, the signal value is less than $3.5 \cdot 10^{-6} \cdot A$.
- The spectral function $X(f)$ is also Gaussian and has similar characteristics as the Gaussian pulse $x(t)$:
- $$X(f) = A \cdot \Delta t \cdot {\rm e}^{ - \pi \left( {f \hspace{0.05cm} \cdot \hspace{0.05cm} \Delta t} \right)^2 }.$$
In the section »Reciprocity Theorem« the analogies of time domain and frequency domain of the Gaussian pulse are discussed in detail.
The following example illustrates the similarities and differences between the Gaussian pulse $x(t)$ and its spectrum $X(f)$.
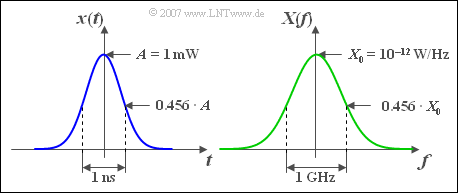
$\text{Example 1:}$ The output power pulse $x(t)$ of a laser for digital optical transmission can be assumed to be Gaussian in the equivalent low-pass range with good approximation.
Let the signal parameters be $A = 1 \,\text{mW}$ and $\Delta t =1 \,\text{ns}$.
This gives the following comparable parameters in the spectral range:
- The maximum $X_0 = X(f=0) = A \cdot \Delta t = 10^{-12} \,\text{W/Hz}$,
- the equivalent bandwidth $\Delta f = 1/\Delta t = 1 \,\text{GHz}$.
Theoretically, the absolute frequency band extends to infinity. However, at $f = 2 \cdot \Delta f = 2\,\text{GHz}$ the spectral function is already reduced by the factor $3.5 \cdot 10^{-6}$ compared to its maximum.
⇒ We would like to draw your attention to two interactive applets on this topic with which you can display the time and frequency domain representations of the Gaussian pulse, rectangular pulse, triangular pulse, trapezoidal pulse and cosine rolloff pulse or the comparable quantities of an LTI system parameterized:
Dirac delta or impulse
In the chapter »Periodic Signals« the »Dirac delta function« was already used to describe the spectrum of a direct current $\rm (DC)$ signal or a harmonic oscillation. However, in Communications Engineering it is also common and extremely advantageous to describe and analyze short-term processes with the help of this mathematical function in the time domain.
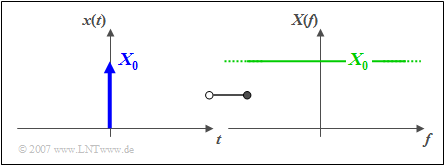
$\text{Definition:}$ A »Dirac delta«, also called»impulse«, is denoted as
- $$x(t) = X_0 \cdot \delta (t),$$
and can be characterised as follows $($see plot$)$:
- The Dirac delta is infinitely narrow ⇒ it holds $x(t)\equiv 0$ for $t \neq 0$ and at time $t = 0$ the Dirac delta is infinitely high.
- If $x(t)$ describes a voltage curve, then the impulse weight $X_0$ has the unit "$\textrm{V} \cdot \textrm{s}$" $($i.e. the unit "$\textrm{V}/\textrm{Hz}$" of a spectral function$)$, since $\delta (t)$ itself has the unit "$1/\textrm{s}$".
- The Fourier transform of the Dirac delta includes all frequencies $f$ equally:
- $$X(f) = X_0 = \rm const.$$
The properties mentioned here are shown in the $($German language$)$ learning video:
»Herleitung und Visualisierung der Diracfunktion« ⇒ "Derivation and visualisation of the Dirac delta function".
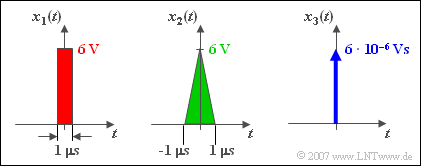
$\text{Example 2:}$ We consider a network with low-pass characteristic and very low cutoff frequency $f_{\rm G} = 10\,\text{ kHz}$. The output signal $y(t)$ does not change significantly when one of the sketched signals $x_1(t)$, $x_2(t)$ or $x_3(t)$ is applied to the input. This result can be interpreted as follows:
- The »equivalent pulse durations« are the same in each case $(\Delta t = 1\, µ\text{s})$ and this is much smaller than $1/f_{\rm G} = 100 \, µ\text{s}$. The actual pulse shape $($rectangle or triangle$)$ has only a minor influence on the output signal $y(t)$.
- Both the rectangle $x_1(t)$ and the triangle $x_2(t)$ can be approximated by the Dirac delta $x_3(t)$. The impulse weight $X_0 = 6 \cdot 10^{-6}\, \text{Vs}$ must be equal to the pulse areas of $x_1(t)$ resp. $x_2(t)$.
- However, a sufficiently small cutoff frequency is required for this approximation. This simplification would not be permitted with $f_{\rm G} = 10 \, \text{MHz}$ ⇒ $1/f_{\rm G} = 100 \, \text{ns}$.
- Even if the Dirac delta is drawn with the same height as the other two pulses, it still has an infinite value at the time $t = 0$.
- For the Dirac delta the impulse area $($»impulse weight«$)$ is always specified. This differs from the other pulse amplitudes already in the unit $($e.g. "Vs" instead of "V"$)$.
Exercises for the chapter
Exercise 3.3: From the Signal to the Spectrum
Exercise 3.3Z: Rectangular Pulse and Dirac Delta