Difference between revisions of "Modulation Methods/Linear Digital Modulation"
| Line 119: | Line 119: | ||
*Für die Grafiken wurden bei ASK (Sinus) und BPSK (Minus–Cosinus) aus Darstellungsgründen verschiedene Trägerphasen gewählt. Diese willkürliche Festlegung ist jedoch keine Einschränkung. Beide Verfahren funktionieren bei anderen Trägerphasen in gleicher Weise. | *Für die Grafiken wurden bei ASK (Sinus) und BPSK (Minus–Cosinus) aus Darstellungsgründen verschiedene Trägerphasen gewählt. Diese willkürliche Festlegung ist jedoch keine Einschränkung. Beide Verfahren funktionieren bei anderen Trägerphasen in gleicher Weise. | ||
| + | ==Demodulation und Detektion von BPSK–Signalen== | ||
| + | Aufgrund der konstanten Hüllkurve des BPSK–Signals muss hier die Demodulation kohärent erfolgen. Es kann dabei vom gleichen Blockschaltbild wie bei der kohärenten ASK–Demodulation ausgegangen werden. Die Grafik zeigt die Signale $q(t), r(t) = s(t), b(t), d(t)$ und $υ(t)$. | ||
| + | |||
| + | |||
| + | [[File: P_ID1693__Mod_T_4_2_S6_ganz_neu.png | Signale bei BPSK–Modulation und kohärenter Demodulation]] | ||
| + | |||
| + | |||
| + | Ein Vergleich mit den entsprechenden ASK–Signalen zeigt: | ||
| + | *Die Rechtecksignale $q(t)$ und $υ(t)$ sind nun bipolar und für das Detektionssignal bei BPSK gilt: | ||
| + | $$d_{\rm BPSK}(t) = | ||
| + | 2 \cdot d_{\rm ASK}(t)-s_0.$$ | ||
| + | *Im betrachteten dämpfungs–, verzerrungs– und rauschfreien Fall sind alle Detektionsabtastwerte $d(ν · T) = ±s_0$. Deshalb muss hier die Entscheiderschwelle $E =$ 0 verwendet werden. | ||
| + | *Man erkennt den doppelten Abstand der BPSK–Detektionsabtastwerte (Kreismarkierungen) von der Schwelle, was sich bezüglich der Fehlerwahrscheinlichkeit entscheidend auswirkt. | ||
Revision as of 14:31, 23 June 2016
Contents
- 1 Unterschiede zwischen analogen und digitalen Modulationsverfahren
- 2 ASK – Amplitude Shift Keying
- 3 Kohärente Demodulation von ASK–Signalen (1)
- 4 Kohärente Demodulation von ASK–Signalen (2)
- 5 Inkohärente Demodulation von ASK–Signalen
- 6 BPSK – Binary Phase Shift Keying
- 7 Demodulation und Detektion von BPSK–Signalen
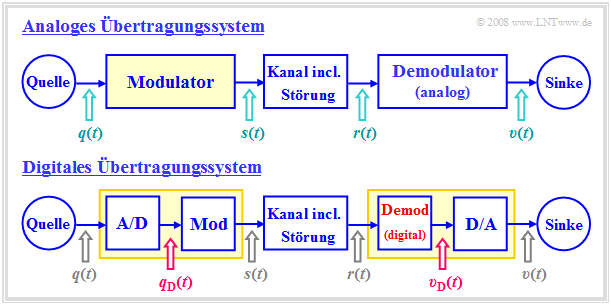
Unterschiede zwischen analogen und digitalen Modulationsverfahren
Die Grafik zeigt oben ein analoges Übertragungssystem und darunter gezeichnet ein Digitalsystem.
Die wesentlichen Unterschiede sind rot hervorgehoben:
- Während beim oberen System am Modulatoreingang das analoge Quellensignal $q(t)$ anliegt, ist beim unteren Digitalsystem das modulierende Signal $q_{\rm D}(t)$ ein Digitalsignal, gekennzeichnet durch die Amplitudenkoeffizienten $a_ν$, den Grundimpuls $g_q(t)$ sowie die Symboldauer $T$:
$$q_{\rm D}(t) = \sum_{\nu=-\infty}^{+\infty}a_\nu \cdot g_q(t - \nu \cdot T) \hspace{0.05cm}.$$
- Die A/D–Wandlung kann z. B. mittels Pulscodemodulation erfolgen und umfasst die Funktionen Abtastung, Quantisierung, Binärcodierung und Signalformung. Der Grundimpuls $g_q(t)$ wird im Folgenden meist als NRZ–rechteckförmig mit Amplitude $s_0$ und Dauer $T$ angenommen, so dass für die Spektralfunktion $G_q(f) = s_0 · T · {\rm si}(π f T)$ mit ${\rm si}(x) = \sin(x)/x$ gilt.
- Die Modulatoren können bei beiden Systemen durchaus gleich sein. Sie verändern einen der drei Signalparameter des Trägersignals $z(t)$ entsprechend dem Modulatoreingangssignal. Die digitalen Varianten von AM, PM und FM heißen Amplitude Shift Keying (ASK), Phase Shift Keying (PSK) und Frequency Shift Keying (FSK).
- Dagegen unterscheidet sich der Demodulator des Digitalsystems grundsätzlich von einem analogen Demodulator durch die erforderliche Entscheiderkomponente (in Hardware oder Software). Das Ausgangssignal $υ_{\rm D}(t)$ ist ebenso wie $q_{\rm D}(t)$ digital. Dieses Signal muss anschließend noch in das analoge Sinkensignal $υ(t)$ D/A–gewandelt werden.
- Das entscheidende Gütekriterium ist bei beiden Systemen das Sinken–SNR als der Quotient der Leistungen von Quellensignal $q(t)$ und Fehlersignal $ε(t) = υ(t) \ – \ q(t).$ Bei einem Digitalsystem begnügt man sich meist mit dem Qualitätsmerkmal Bitfehlerquote (engl.: Bit Error Rate, BER), das sich auf die beiden Digitalsignale $q_{\rm D}(t)$ und $υ_{\rm D}(t)$ bezieht. Diese ist in ein SNR umrechenbar.
ASK – Amplitude Shift Keying
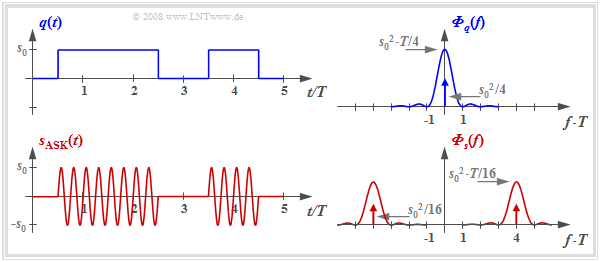
Die Grafik zeigt das digitale Quellensignal $q(t)$ – auf den Index „D” wird ab sofort verzichtet – sowie das ASK–Sendesignal $s_{\rm ASK}(t) = q(t) · \sin(2π · f_{\rm T} · t)$, wobei hier von unipolaren Amplitudenkoeffizienten $a_ν ∈$ {0, 1} und einem sinusförmigen Träger ausgegangen wird. Dieses Verfahren wird insbesondere bei optischen Übertragungssystemen eingesetzt (da es bekanntlich keine negativen Lichtimpulse gibt) und ist auch unter der Bezeichnung On–Off–Keying bekannt.
In der rechten Bildhälfte sind – allerdings nicht maßstäblich – die dazugehörigen Leistungsdichtespektren (abgekürzt: LDS) dargestellt. Bei rechteckförmigem Grundimpuls $g_q(t)$ und gleichwahrscheinlichen unipolaren Amplitudenkoeffizienten gilt:
$$\begin{align*}{{\it \Phi}_{q}(f)}& = \frac{{s_0}^2 \cdot T}{4} \cdot {\rm si}^2 (\pi f T) + \frac{{s_0}^2 }{4} \cdot \delta (f)\hspace{0.05cm},\\ {{\it \Phi}_{s}(f)}& = \frac{1}{4} \cdot \left [ {{\it \Phi}_{q}(f- f_{\rm T})}+ {{\it \Phi}_{q}(f+ f_{\rm T})}\right]\hspace{0.05cm}.\end{align*}$$
Zu diesen Gleichungen ist zu bemerken:
- Der Gleichanteil $m_q = s_0/2$ des Quellensignals führt im Leistungsdichtespektrum $ϕ_q(f)$ zu einer Diracfunktion bei der Frequenz $f = 0$ mit dem Gewicht ${s_0}^2/4$.
- Das Leistungsdichtespektrum des ASK–Sendesignals ist gleich $ϕ_s(f) = ϕ_q(f) ∗ ϕ_z(f)$, wobei sich das LDS $ϕ_z(f)$ des Trägersignals $Z(t)$ aus zwei Diracfunktionen bei $±f_{\rm T}$ mit jeweiligem Gewicht 1/4 zusammensetzt. Die Gleichung gilt auch bei anderer Trägerphase, „∗” beschreibt die Faltung.
- Das Leistungsdichtespektrum $ϕ_s(f)$ ist bis auf die Verschiebung um $±f_{\rm T}$ formgleich mit $ϕ_q(f)$. Deshalb gehört ASK zu den linearen digitalen Modulationsverfahren.
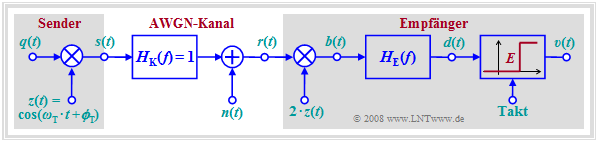
Kohärente Demodulation von ASK–Signalen (1)
Die Grafik zeigt das Blockschaltbild eines ASK–Systems inklusive der Empfängerkomponenten. Das Quellensignal $q(t)$ sei NRZ–rechteckförmig und unipolar, das heißt, es gilt $a_ν ∈$ {0, 1}. Der Kanal sei zunächst ideal, gekennzeichnet durch $H_{\rm K}(f) =$ 1 und $n(t) =$ 0 ⇒ $r(t) = s(t)$.
Die Demodulation erfolgt hier kohärent mittels Synchrondemodulator, dessen Funktionsweise bereits bei den analogen Modulationsverfahren AM und PM beschrieben wurde.
Zusammenfassend lässt sich sagen:
- Beim Empfänger wird das gleiche Trägersignal zugesetzt wie beim Sender, jedoch mit doppelter Amplitude. $z(t)$ bezeichnet den Träger beim Sender und $2 · z(t)$ den Träger beim Empfänger.
- Nach der Multiplikation folgt ein geeignet dimensionierter Tiefpass mit dem Frequenzgang $H_{\rm E}(f)$, der die höherfrequenten Anteile des Signals $b(t)$ entfernt.
- Schließlich wird das Detektionssignal $d(t)$ zu den Detektionszeitpunkten $ν · T$ abgetastet und mit Hilfe eines Schwellenwertentscheiders mit der Entscheiderschwelle $E = {s_0}/2$ entschieden.
- Das Sinkensignal $υ(t)$ am Ausgang des Entscheiders ist rechteckförmig und im rauschfreien Fall (oder bei nur kleinen Rauschstörungen) bis auf die Laufzeit $T/2$ gleich dem Quellensignal $q(t)$.
Zu beachten ist: Eine kohärente Demodulation erfordert, dass dem Empfänger die Trägerfrequenz $f_{\rm T}$ und die Trägerphase $ϕ_{\rm T}$ exakt bekannt sind. Der Empfänger muss diese beiden Größen aus dem Empfangssignal $r(t)$ extrahieren, was bei starken Kanalverzerrungen und großen Rauschstörungen durchaus aufwändig sein kann. Solche Realisierungsaspekte werden zum Beispiel in der Aufgabe A4.8 zu diesem Kapitel behandelt.
Kohärente Demodulation von ASK–Signalen (2)
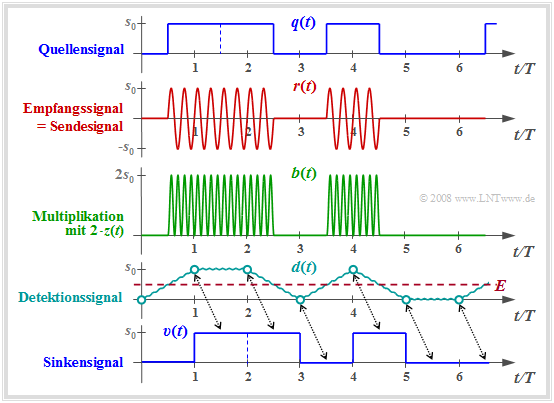
Die Grafik zeigt die im ASK–Blockschaltbild genannten Signale bei idealem Kanal: $H_{\rm K}(f) =$ 1, $n(t) =$ 0.
Die einzelnen Signalverläufe können wie folgt interpretiert werden:
- Das Sendesignal $s(t)$ ist das Produkt aus dem unipolaren Quellensignal $q(t)$ und dem Trägersignal $z(t) = \sin(2πf_{\rm T}t)$, wobei hier $f_{\rm T} = 4/T$ gilt (nur jeweils vier Schwingungen pro Symboldauer).
- Das Empfangssignal $r(t) = s(t)$ wird zunächst mit dem Träger $z_{\rm E}(t) = 2 · \sin(2πf_{\rm T}t)$ ⇒ doppelte Amplitude gegenüber $z(t)$, kein Frequenz– und Phasenversatz – multipliziert. Damit ergibt sich:
$$b(t) = 2 \cdot z(t)\cdot r(t)= 2 \cdot z^2(t)\cdot q(t) = q(t) \cdot \left [ 1 - \cos(4\pi f_{\rm T} t)\right] \hspace{0.05cm}.$$
- Das TP–Filter mit dem Frequenzgang $H_{\rm E}(f) = {\rm si}(πf_{\rm T}T)$ und dementsprechend rechteckförmiger Impulsantwort $h_{\rm E}(t)$ formt aus dem Signal $b(t)$ das Detektionssignal $d(t) = b(t) \star h_{\rm E}(t)$.
- $h_{\rm E}(t)$ ist an den rechteckförmigen Grundimpuls $g_q(t)$ angepasst; man spricht vom sog. Matched–Filter ⇒ bestmöglicher Kompromiss zwischen Entzerrung und Rauschleistungsbegrenzung.
- Ohne Rauschen gilt $d(νT) = q(νT) ∈$ {0, $s_0$}. Bei (moderaten) Rauschstörungen ist mit großer Wahrscheinlichkeit $d(νT) > s_0/2,$ falls $a_ν = +1$, und es wird $d(νT) < s_0/2$ für $a_ν = 0$ gelten.
- Der Schwellenwertentscheider gewinnt aus dem Vergleich der Detektionsabtastwerte $d(νT)$ mit der Entscheiderschwelle $E = s_0/2$ das Sinkensignal $υ(t)$, das bei fehlerfreier Entscheidung bis auf die Laufzeit $T/2$ identisch mit $q(t)$ ist.
Inkohärente Demodulation von ASK–Signalen
Wir gehen weiter von ASK–Modulation sowie dem idealen (das heißt: verzerrungs–, dämpfungs– und rauschfreien) Übertragungskanal aus, so dass gilt: $$r(t) = s(t) = q(t) \cdot \cos(2 \pi \cdot f_{\rm T} \cdot t + \phi_{\rm T})\hspace{0.05cm}.$$ Weiter wird für diesen Abschnitt vorausgesetzt, dass dem Empfänger zwar die Trägerfrequenz $f_{\rm T}$, nicht jedoch die Trägerphase $ϕ_{\rm T}$ bekannt ist. Üblich ist, auch diesen Demodulator als inkohärent zu bezeichnen.
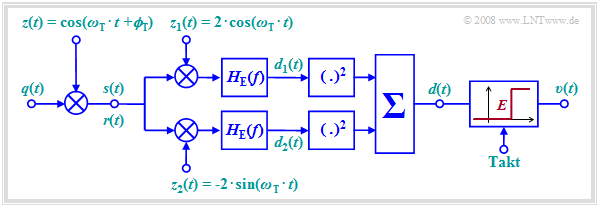
Die Grafik zeigt einen solchen inkohärenten Demodulator, dessen Funktionsweise hier nur stichpunktartig angegeben werden soll. Das Demodulationsergebnisse ist unabhängig von der Trägerphase $ϕ_{\rm T}$, die der Empfänger nicht kennt.
- Die Signale $d_1(t)$ und $d_2(t)$ nach den beiden Matched–Filtern mit jeweiligen Frequenzgang $H_{\rm E}(f)$ sind formgleich mit dem Detektionssignal $d_{\rm koh}(t)$ entsprechend der Grafik des letzten Abschnitts, aber gegenüber diesem im Allgemeinen wegen der fehlenden Phasenanpassung gedämpft:
$$d_1(t) = d_{\rm koh}(t) \cdot \cos( \phi_{\rm T}), \hspace{0.2cm}d_2(t) = -d_{\rm koh}(t) \cdot \sin( \phi_{\rm T}) \hspace{0.05cm}.$$
- Ist der Amplitudenkoeffizient $a_ν =$ 0, so sind im rauschfreien Fall die beiden Signalwerte $d_1(ν · T)$ und $d_2(ν · T)$ jeweils 0. Andernfalls $(a_ν = 1)$ gilt für den Zeitpunkt $ν · T$:
$$d_1(\nu \cdot T) = s_{\rm 0} \cdot \cos( \phi_{\rm T}), \hspace{0.2cm}d_2(\nu \cdot T) = -s_{\rm 0} \cdot \sin( \phi_{\rm T}) \hspace{0.05cm}.$$
- Nach Quadrierung der zwei Teilsignale erhält man für das Summensignal:
$$d(\nu \cdot T) = \left\{ \begin{array}{c} 0 \\ {s_0}^2 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}a_\nu = 0, \\ {\rm falls}\hspace{0.15cm}a_\nu = 1. \\ \end{array}$$
- Durch die Schwellenwertentscheidung – sinnvollerweise mit der Entscheiderschwelle $E = {s_0}^2/4$ – können die Amplitudenkoeffizienten $a_ν$ entschieden werden. Allerdings ergibt sich eine etwas größere Bitfehlerwahrscheinlichkeit als bei kohärenter Demodulation.
BPSK – Binary Phase Shift Keying
Bei analoger Phasenmodulation lautet das Sendesignal entsprechend Kapitel 3.1 allgemein: $$s_{\rm PM}(t) = s_0 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T}+ K_{\rm PM} \cdot q(t))\hspace{0.05cm}.$$ Bei bipolarem Quellensignal ⇒ $a_ν ∈$ {–1, +1}, der angenommenen Trägerphase $ϕ_{\rm T} = π$ (180°) und mit der geeignet dimensionierten Modulatorkonstanten $K_{\rm PM} = π/(2s_0)$ ergibt sich im $ν$–ten Zeitintervall: $$s_{\rm BPSK}(t) = \left\{ \begin{array}{c} s_0 \cdot \cos(2 \pi f_{\rm T} t + \pi+ \pi/2) \\ s_0 \cdot \cos(2 \pi f_{\rm T} t + \pi- \pi/2) \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}a_\nu = +1, \\ {\rm falls}\hspace{0.15cm}a_\nu = -1. \\ \end{array}$$ Diese Gleichung für die binäre Phasenmodulation (BPSK) lässt sich wie folgt umformen: $$s_{\rm BPSK}(t) = a_\nu \cdot s_0 \cdot \sin(2 \pi f_{\rm T} t ) = \left\{ \begin{array}{c} s_0 \cdot \sin(2 \pi f_{\rm T} t ) \\ -s_0 \cdot \sin(2 \pi f_{\rm T} t ) \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}a_\nu = +1, \\ {\rm falls}\hspace{0.15cm}a_\nu = -1. \\ \end{array}$$
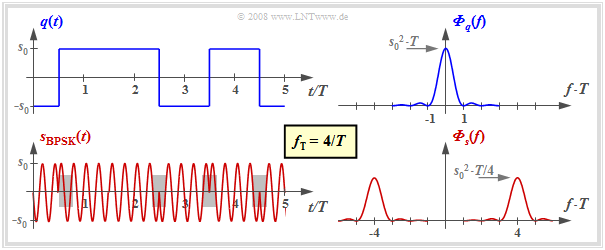
In der Grafik sind die Signale und die dazugehörigen Leistungsdichtespektren skizziert. Man erkennt:
- Das BPSK–Signal lässt sich wie das ASK–Signal als Produkt von Quellensignal $q(t)$ und Trägersignal $z(t)$ darstellen. Der einzige Unterschied liegt in den bipolaren Amplitudenkoeffizienten $a_ν ∈$ {–1, +1} gegenüber den unipolaren Koeffizienten (0 oder 1) bei ASK.
- Im Gegensatz zur ASK ist bei der BPSK – wie bei jeder Form von Phasenmodulation – die Hüllkurve konstant. Die Information wird hier durch die Phasensprünge innerhalb des Sendesignals $s(t)$ übermittelt (graue Hinterlegungen in der Grafik).
- Die Leistungsdichtespektren bei BPSK unterscheiden sich von denen bei ASK lediglich durch die fehlenden Diracfunktionen (da nun $q(t)$ keinen Gleichanteil beinhaltet) sowie durch den Faktor 4 bezüglich der kontinuierlichen LDS–Anteile.
- Daraus folgt weiter, dass die binäre Phasenmodulation zu den linearen Modulationsverfahren gezählt werden kann. Im Allgemeinen ist nämlich die (analoge) Phasenmodulation bis auf wenige Ausnahmen hinsichtlich des Quellensignals nichtlinear.
- Für die Grafiken wurden bei ASK (Sinus) und BPSK (Minus–Cosinus) aus Darstellungsgründen verschiedene Trägerphasen gewählt. Diese willkürliche Festlegung ist jedoch keine Einschränkung. Beide Verfahren funktionieren bei anderen Trägerphasen in gleicher Weise.
Demodulation und Detektion von BPSK–Signalen
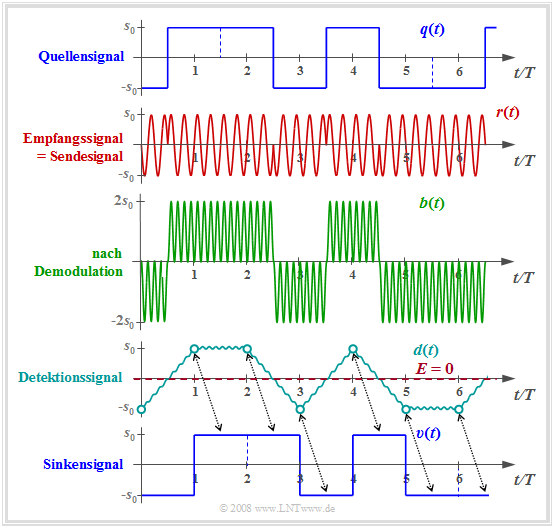
Aufgrund der konstanten Hüllkurve des BPSK–Signals muss hier die Demodulation kohärent erfolgen. Es kann dabei vom gleichen Blockschaltbild wie bei der kohärenten ASK–Demodulation ausgegangen werden. Die Grafik zeigt die Signale $q(t), r(t) = s(t), b(t), d(t)$ und $υ(t)$.
Ein Vergleich mit den entsprechenden ASK–Signalen zeigt:
- Die Rechtecksignale $q(t)$ und $υ(t)$ sind nun bipolar und für das Detektionssignal bei BPSK gilt:
$$d_{\rm BPSK}(t) = 2 \cdot d_{\rm ASK}(t)-s_0.$$
- Im betrachteten dämpfungs–, verzerrungs– und rauschfreien Fall sind alle Detektionsabtastwerte $d(ν · T) = ±s_0$. Deshalb muss hier die Entscheiderschwelle $E =$ 0 verwendet werden.
- Man erkennt den doppelten Abstand der BPSK–Detektionsabtastwerte (Kreismarkierungen) von der Schwelle, was sich bezüglich der Fehlerwahrscheinlichkeit entscheidend auswirkt.