Difference between revisions of "Modulation Methods/General Description of OFDM"
| Line 24: | Line 24: | ||
==Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (2)== | ==Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (2)== | ||
Hier nochmals der OFDM–Sender zur Verdeutlichung des dahinter stehenden Prinzips. | Hier nochmals der OFDM–Sender zur Verdeutlichung des dahinter stehenden Prinzips. | ||
| + | |||
''Hinweis:'' In diesem Bild wurde die Darstellung des „nullten” Zweiges $(\mu = 0)$, der den Gleichanteil darstellt, bewusst weggelassen, da dieser häufig zu Null gesetzt wird ⇒ für alle Rahmen $k$ gilt $a_{0, k} =$ 0. | ''Hinweis:'' In diesem Bild wurde die Darstellung des „nullten” Zweiges $(\mu = 0)$, der den Gleichanteil darstellt, bewusst weggelassen, da dieser häufig zu Null gesetzt wird ⇒ für alle Rahmen $k$ gilt $a_{0, k} =$ 0. | ||
| − | [[File: | + | [[File:P_ID1636__Mod_T_5_5_S1a_neu.png | Prinzip eines OFDM-Senders]] |
| + | |||
| + | Das Sendesignal ist nun die additive Überlagerung der einzelnen Teilsignale. Die Betrachtung erfolgt hier und auch im Folgenden im äquivalenten Tiefpassbereich, wobei auf den Index „TP” verzichtet wird. | ||
| + | Das Impulsformfilter $g_s(t)$ ist ein auf den Bereich $0 ≤ t < T$ begrenztes Rechteck der Höhe $s_0$. Wir nennen $T$ die Symboldauer und bezeichnen den Kehrwert $f_0 = 1/T$ als die Grundfrequenz. | ||
| + | Fasst man dieses Filter nun mit der jeweiligen Modulation zu | ||
| + | $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$ | ||
| + | mit $\mu ∈$ {0, ... , $N$–1} zusammen, so ergibt sich das OFDM–Sendesignal $s_k(t)$ im $k$–ten Zeitintervall: | ||
| + | $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$$ | ||
| + | Das gesamte OFDM–Sendesignal unter Berücksichtigung aller Zeitintervalle lautet dann: | ||
| + | $$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )} }.$$ | ||
| + | $T_{\rm R}$ bezeichnet die Rahmendauer. Innerhalb dieser Zeit liegen die gleichen Daten am Eingang an und nach $T_{\rm R}$ folgt der nächste Rahmen. Für die Symboldauer muss gelten: $T ≤ T_{\rm R}$. Zunächst gelte $T = T_{\rm R}$. | ||
Revision as of 17:24, 2 July 2016
Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (1)
Orthogonal Frequency Division Multiplex (OFDM) ist ein digitales Mehrträger–Modulationsverfahren mit folgenden Eigenschaften:
- Statt eines breitbandigen, stark modulierten Signals werden zur Datenübertragung eine Vielzahl schmalbandiger, zueinander orthogonaler Unterträger verwendet. Dies ermöglicht unter anderem die Anpassung an einen frequenzselektiven Kanal.
- Die Modulation der Unterträger selbst erfolgt bei OFDM üblicherweise durch eine herkömmliche Quadratur–Amplitudenmodulation (QAM) oder durch binäre Phasenmodulation (BPSK), wobei sich die einzelnen Träger hinsichtlich der Modulationsart durchaus unterscheiden können.
- Unterschiede im Modulationsgrad führen dabei zu verschieden hohen Datenraten der Unterträger. Das heißt also, dass ein hochratiges Quellensignal zur Übertragung in mehrere Signale von deutlich niedrigerer Symbolrate aufgespaltet werden muss.
Die Möglichkeit, für verschiedene Teilbänder unterschiedlich robuste Modulationsverfahren einzusetzen, ist einer der großen Vorteile von OFDM. Hierauf wird in den Abschnitten OFDM für 4G–Netze und Digital Subscriber Line (DSL) noch näher eingegangen.
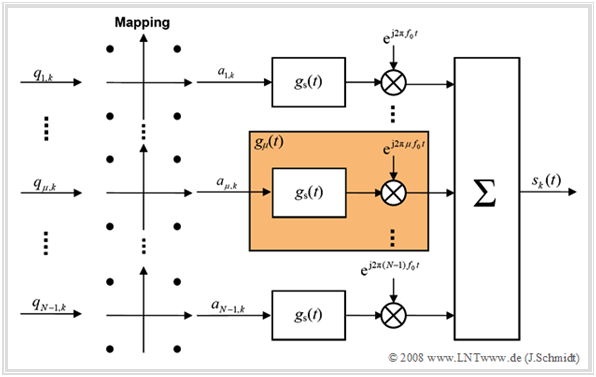
Die Grafik zeigt das Grundprinzip eines OFDM–Senders.
- Die $N$–1 Teile des zur Zeit $k$ anliegenden Datenstroms $〈q_{\mu,k}〉$ werden in diesem durch die Grafik verdeutlichten Beispiel 4–QAM–codiert, indem jeweils zwei Bit zusammengefasst werden.
- Danach wird die im Allgemeinen komplexe Amplitude $a_{\mu,k}$ (mit Laufvariablen $\mu = 1, ... , N–1$) impulsgeformt und mit dem $\mu$–ten Vielfachen der Grundfrequenz $f_0$ moduliert.
Das Prinzip von OFDM – Systembetrachtung im Zeitbereich (2)
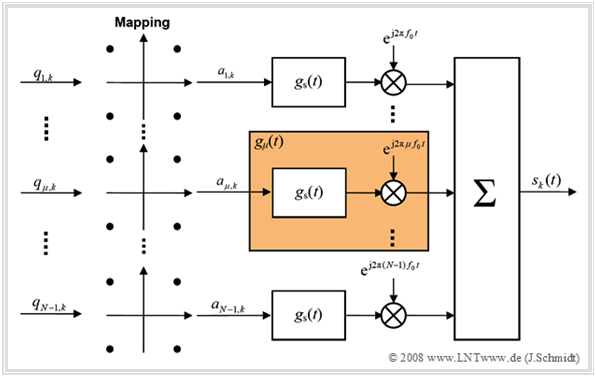
Hier nochmals der OFDM–Sender zur Verdeutlichung des dahinter stehenden Prinzips.
Hinweis: In diesem Bild wurde die Darstellung des „nullten” Zweiges $(\mu = 0)$, der den Gleichanteil darstellt, bewusst weggelassen, da dieser häufig zu Null gesetzt wird ⇒ für alle Rahmen $k$ gilt $a_{0, k} =$ 0.
Das Sendesignal ist nun die additive Überlagerung der einzelnen Teilsignale. Die Betrachtung erfolgt hier und auch im Folgenden im äquivalenten Tiefpassbereich, wobei auf den Index „TP” verzichtet wird.
Das Impulsformfilter $g_s(t)$ ist ein auf den Bereich $0 ≤ t < T$ begrenztes Rechteck der Höhe $s_0$. Wir nennen $T$ die Symboldauer und bezeichnen den Kehrwert $f_0 = 1/T$ als die Grundfrequenz.
Fasst man dieses Filter nun mit der jeweiligen Modulation zu $$g_\mu (t) = \left\{ \begin{array}{l} s_0 \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j2 \pi}} {\kern 1pt} \mu f_0 t} \quad 0 \le t < T, \\ 0 \quad \quad \quad \quad \quad {\rm sonst} \\ \end{array} \right.$$ mit $\mu ∈$ {0, ... , $N$–1} zusammen, so ergibt sich das OFDM–Sendesignal $s_k(t)$ im $k$–ten Zeitintervall: $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )}.$$ Das gesamte OFDM–Sendesignal unter Berücksichtigung aller Zeitintervalle lautet dann: $$s(t) = \sum\limits_{k = - \infty }^{+\infty} {\sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )} }.$$ $T_{\rm R}$ bezeichnet die Rahmendauer. Innerhalb dieser Zeit liegen die gleichen Daten am Eingang an und nach $T_{\rm R}$ folgt der nächste Rahmen. Für die Symboldauer muss gelten: $T ≤ T_{\rm R}$. Zunächst gelte $T = T_{\rm R}$.