Difference between revisions of "Modulation Methods/Implementation of OFDM Systems"
| Line 99: | Line 99: | ||
Aus diesem Grund soll im Folgenden der Ansatz „Guard–Lücke” nicht mehr weiter betrachtet werden. Vielmehr wird nachfolgend eine bessere Alternative vorgestellt. | Aus diesem Grund soll im Folgenden der Ansatz „Guard–Lücke” nicht mehr weiter betrachtet werden. Vielmehr wird nachfolgend eine bessere Alternative vorgestellt. | ||
| + | |||
| + | ==Zyklisches Präfix (1)== | ||
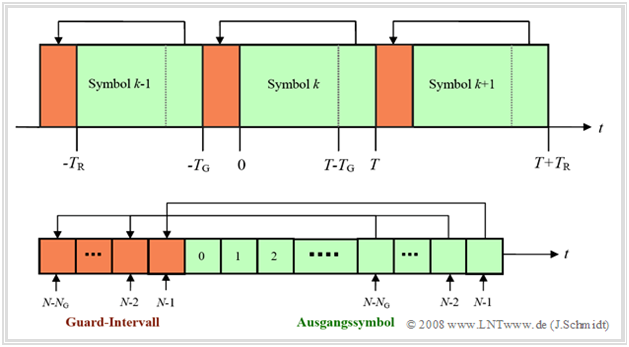
| + | Eine besser geeignete Lösung für das beschriebene Problem ist die Einführung einer zyklischen Erweiterung der Sendesymbole im so genannten ''Guard–Intervall'' der Länge $T_{\rm G}$. Dafür wird das Ende eines Symbols im Zeitabschnitt $T – T_{\rm G} ≤ t < T$ dem eigentlichen Symbol erneut vorangestellt. Dieses Verfahren erzeugt somit ein zyklisches Präfix. | ||
| + | |||
| + | |||
| + | [[File:P_ID1645__Mod_T_5_6_S5a_neu.png | Prinzip des zyklischen Präfixes]] | ||
| + | |||
| + | |||
| + | Die Intervalldauer steigt dabei wie bei der Guard–Lücke von der ursprünglichen Symboldauer $T$ auf die neue Rahmendauer $T_{\rm R} = T + T_{\rm G}$. Die neue Anzahl der Abtastwerte des erweiterten zeitdiskreten Signals im $k$–ten Intervall beträgt dann: | ||
| + | $$N_{\rm{gesamt}} = N + N_{\rm{G}} = N \cdot (1 + T_{\rm{G}} /T) .$$ | ||
| + | Die Anzahl der Träger und die Anzahl der Nutz–IDFT–Werte ist weiterhin $N$. Die Erweiterung wird hier lediglich durch eine Wiederholung von Werten als Guard–Intervall erzielt. | ||
Revision as of 19:02, 2 July 2016
Contents
OFDM mittels diskreter Fouriertransformation
Betrachten wir nun erneut die sich zeitlich nicht überlappenden Sendesignalrahmen $$s_k (t) = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot g_\mu (t - k \cdot T_{\rm{R}} )},$$ wobei $k$ die Rahmennummer angibt. Diese besitzen zu den Abtastzeiten $k · T_{\rm R} + ν · T_{\rm A}$ mit $0 ≤ ν < N$ und $T_{\rm A} = T/N$ die Abtastwerte $$s_{\nu ,k} = \sum\limits_{\mu = 0}^{N - 1} {a_{\mu ,k} \cdot {\rm{e}}^{ {\kern 1pt} {\rm{j\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi}} {\kern 1pt}\cdot \hspace{0.03cm}\nu \hspace{0.03cm}\cdot \hspace{0.03cm}{\mu}/{N}} }.$$ Mit der Umbenennung $s_{ν,k} = d_{ν,k}$ und $a_{\mu,k} = D_{\mu,k}$ entspricht diese Gleichung exakt der Inversen Diskreten Fouriertransformation – abgekürzt IDFT – im jeweils $k$–ten Intervall: $$\quad d_{\nu ,k} = \sum\limits_{\mu = 0}^{N - 1} {D_{\mu ,k} \cdot w^{ - \nu \hspace{0.03cm}\cdot \hspace{0.03cm} \mu } } \quad {\rm{mit}} \quad w = {\rm{e}}^{ - {\rm{j}} {\rm{\hspace{0.03cm}\cdot \hspace{0.03cm}2\pi}}/N}.$$ Hierbei sind $d_{ν,k}$ die Zeitabtastwerte und $D_{ν,k}$ die diskreten Spektralkoeffizienten. Die Gleichung für den Übergang von der diskreten Zeit– zur diskreten Spektralfunktion – also die DFT – lautet: $$\quad D_{\mu ,k} = \frac{1}{N}\cdot \sum\limits_{\nu = 0}^{N - 1} {d_{\nu ,k} \cdot w^{\hspace{0.05cm}\nu \hspace{0.03cm}\cdot \hspace{0.03cm}\mu } }.$$
Weiterhin gilt:
- Die Koeffizienten $d_{ν,k}$ und $D_{μ,k}$ sind mit der Stützstellenanzahl $N$ periodisch. Zudem sind sie im Allgemeinen komplexwertig.
- DFT und IDFT sind prinzipiell gleich aufgebaut und unterscheiden sich nur durch das Vorzeichen im Exponenten des komplexen Drehfaktors $w$ sowie den Normierungsfaktor $1/N$ bei der DFT.
Hinweis: Das Flash–Modul Diskrete Fouriertransformation verdeutlicht die Eigenschaften der DFT.
Mit Hilfe der Schnellen Fouriertransformation (Fast Fourier Transform, FFT) ergibt sich die Möglichkeit einer sehr effizienten Realisierung des Mehrträgersystems.
Anmerkung: Für die Verwendung von FFT/IFFT muss die Anzahl der Stützstellen (bzw. Abtastwerte) im Zeit– und Frequenzbereich jeweils eine Zweierpotenz sein. Unter dieser Voraussetzung ist mit den verschiedenen bekannten Algorithmen zur Umsetzung der FFT eine Berechnung mit der Komplexität ${\rm O}(N · {\rm ld}(N))$ möglich.
OFDM–Sender
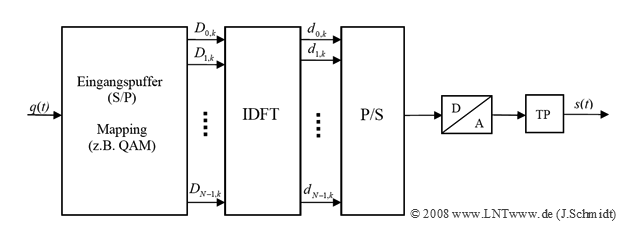
Die Grafik zeigt das Blockschaltbild eines OFDM–Senders mittels IDFT. Der Index $k$ kennzeichnet wieder den Zeitrahmen. Man erkennt aus dieser Darstellung:
- Im Eingangspuffer wird das Quellensignal $q(t)$ implizit seriell/parallel (S/P) gewandelt und danach eine Signalraumzuordnung auf die $N$ Spektralkoeffizienten $D_{\mu,k}$ vorgenommen.
- Bei einem 4–QAM–Mapping ergeben jeweils zwei Quellensymbole zusammen einen komplexen Koeffizienten $D_{\mu,k}$, der vier verschiedene Werte annehmen kann.
- Die so erzeugten Spektralkoeffizienten $D_{\mu,k}$ werden anschließend dem IDFT–Block zugeführt, der daraus die Zeitbereichswerte $d_{ν,k}$ generiert.
- Diese werden wieder parallel/seriell gewandelt. Nach der darauf folgenden D/A–Wandlung und einer Tiefpassfilterung erhält man schließlich das Sendesignal $s(t)$ im äquivalenten Tiefpassbereich.
Fazit: Die Inverse Diskrete Fouriertransformation (IDFT) ersetzt beim OFDM–Sender die sehr aufwändige parallele Modulation der $N$ orthogonalen Träger. Durch die Realisierung als IFFT (Inverse Fast Fourier Transform) ergibt sich eine weitere Aufwandsreduktion.
OFDM–Empfänger
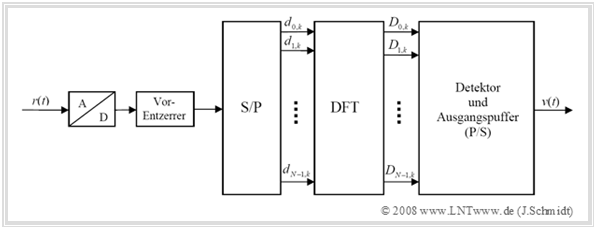
Die folgende Grafik zeigt das Blockschaltbild eines OFDM–Empfängers mittels DFT.
Die wesentlichen Schritte dabei sind:
- Das Eingangssignal $r(t)$ des Empfängers wird zunächst digitalisiert (A/D–Wandlung). Darauf folgt eine Vorentzerrung im Zeitbereich (optional), zum Beispiel mittels Entscheidungsrückkopplung (Decision Feedback Equalization, DFE) oder Viterbi–Algorithmus.
- Anzumerken ist, dass die entscheidende Entzerrung jedoch im Frequenzbereich erfolgt. Diese wird erst im Abschnitt OFDM–Entzerrung am Kapitelende exemplarisch erläutert und ist in obiger Grafik nicht berücksichtigt.
- Nach der Seriell/Parallel–Wandlung (S/P) werden die diskreten Zeitwerte $d_{ν,k}$ dem DFT–Block zugeführt. Die erzeugten Spektralabtastwerte $D_{\mu,k}$ werden durch den QAM–Detektor decodiert und im Ausgangspuffer implizit parallel/seriell gewandelt, woraus das Sinkensignal $υ(t)$ hervorgeht.
- Zu beachten ist allerdings, dass sich die empfängerseitigen Koeffizienten $d_{ν,k}$ und $D_{\mu,k}$ aufgrund von Kanalverzerrungen und Rauschen von den entsprechenden Größen des OFDM–Senders durchaus unterscheiden können, was bei der gewählten Nomenklatur nicht zum Ausdruck kommt.
- Die Koeffizienten $â_{\mu,k}$ des Sinkensignals $υ(t)$ sind nur bei fehlerfreier Detektion identisch mit den Koeffizienten $a_{\mu,k}$ des Quellensignals $q(t)$. Im Allgemeinen unterscheiden sich diese, was durch die Symbolfehlerrate erfasst wird.
Fazit: In der Praxis ersetzt die Diskrete Fouriertransformation (DFT) die sehr aufwändige parallele Demodulation der $N$ orthogonalen Träger. Durch die Realisierung als FFT (Fast Fourier Transform) ergibt sich eine weitere Aufwandsreduktion.
Guard–Lücke zur Verminderung der Impulsinterferenzen (1)
Die Orthogonalität der OFDM–Träger geht bei der Übertragung über einen frequenzselektiven Kanal verloren. Die daraus resultierende Interferenz zwischen den einzelnen Trägern bezeichnet man als Intercarrier–Interferenz (ICI). Die Übertragung über einen solchen Mehrwegekanal bewirkt letztlich aber auch eine Überlagerung aufeinander folgender Symbole und damit Impulsinterferenzen (engl. Intersymbol Interference, ISI).
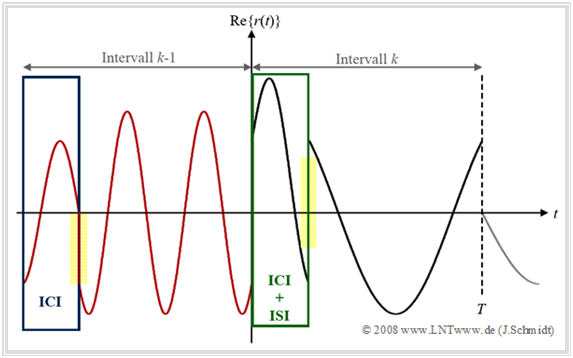
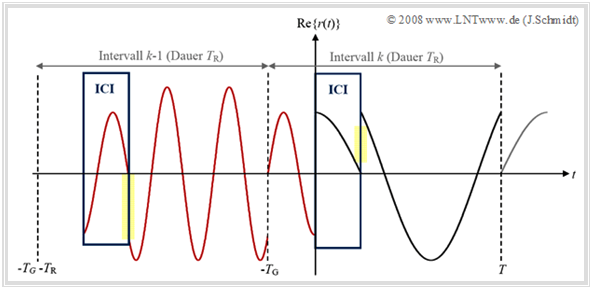
Die Grafik zeigt den Realteil eines OFDM–Empfangssignals im äquivalenten Tiefpassbereich nach der Übertragung über einen rauschfreien Mehrwegekanal mit den Parametern
- für den Pfad 0: Dämpfung $h_0 =$ 0.5; Verzögerung $τ_0/T =$ 0,
- für den Pfad 1: Dämpfung $h_1 =$ 0.5; Verzögerung $τ_1/T =$ 0.25.
Schwarz gezeichnet ist der mit „Plus–Eins” belegte Träger der Frequenz $1 · f_0$ des Intervalls $k$. Der mit „Minus–Eins” gewichtete Träger mit der Frequenz $3 · f_0$ im vorherigen Intervall $(k–1)$ ist rot dargestellt. Andere Intervalle und Träger werden nicht berücksichtigt. Man erkennt aus dieser Skizze:
- Die Einschwingvorgänge zu Symbolbeginn führen zu Intercarrier–Interferenz (ICI) im Spektrum. Im Zeitbereich erkennt man ICI an den auftretenden Sprüngen (in der Grafik gelb markiert). Dadurch geht die Orthogonalität bezüglich der Frequenzstützstellen verloren.
- Weiter erkennt man Impulsinterferenzen (ISI) im grün markierten Zeitintervall $0 ≤ t < τ_1$: Das Vorgängersymbol $k–1$ (Frequenz $3 · f_0$) stört das Symbol $k$ (Frequenz $1 · f_0$).
Guard–Lücke zur Verminderung der Impulsinterferenzen (2)
Ein erster möglicher Lösungsansatz für das zweite Problem (ISI) ist die Einführung einer Guard–Lücke der Länge $T_{\rm G}$. Dabei wird das Signal zwischen zwei Symbolen für die Dauer der Schutzzeit $T_{\rm G}$ zu Null gesetzt. Mögliche Impulsnachläufer des Symbols $k–1$ reichen dadurch nicht mehr in das darauffolgende Symbol $(k)$ hinein, sofern die Guard–Lücke „breiter” als die maximale Kanalverzögerung gewählt wird. Die neue Rahmendauer $T_{\rm R}$ – also der Abstand der Sendesymbole – ergibt sich damit zu $T_{\rm R} = T + T_{\rm G}$.
Die untere Grafik zeigt wieder den Realteil des OFDM–Empfangssignals, aber nun mit Guard–Lücke. Die Systemparameter des letzten Abschnitts wurden beibehalten und zusätzlich $T_{\rm G} = T/4$ gesetzt, was bei dem gewählten Parametersatz dem Grenzfall $T_{\rm G} = τ_{\rm max}$ entspricht.
Diese Grafik zeigt: Durch die Verwendung einer Guard–Lücke entsprechender Breite können zwar Impulsinterferenzen (ISI) vermieden werden, Intercarrier–Interferenz (ICI) lässt sich dadurch jedoch nicht verhindern, da die Symbole weiterhin eine Einschwingphase und damit Sprünge aufweisen.
Aus diesem Grund soll im Folgenden der Ansatz „Guard–Lücke” nicht mehr weiter betrachtet werden. Vielmehr wird nachfolgend eine bessere Alternative vorgestellt.
Zyklisches Präfix (1)
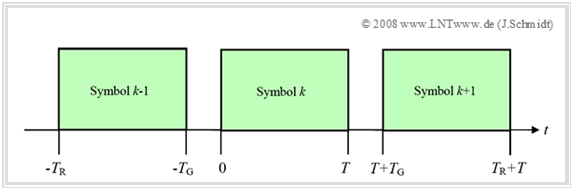
Eine besser geeignete Lösung für das beschriebene Problem ist die Einführung einer zyklischen Erweiterung der Sendesymbole im so genannten Guard–Intervall der Länge $T_{\rm G}$. Dafür wird das Ende eines Symbols im Zeitabschnitt $T – T_{\rm G} ≤ t < T$ dem eigentlichen Symbol erneut vorangestellt. Dieses Verfahren erzeugt somit ein zyklisches Präfix.
Die Intervalldauer steigt dabei wie bei der Guard–Lücke von der ursprünglichen Symboldauer $T$ auf die neue Rahmendauer $T_{\rm R} = T + T_{\rm G}$. Die neue Anzahl der Abtastwerte des erweiterten zeitdiskreten Signals im $k$–ten Intervall beträgt dann:
$$N_{\rm{gesamt}} = N + N_{\rm{G}} = N \cdot (1 + T_{\rm{G}} /T) .$$
Die Anzahl der Träger und die Anzahl der Nutz–IDFT–Werte ist weiterhin $N$. Die Erweiterung wird hier lediglich durch eine Wiederholung von Werten als Guard–Intervall erzielt.