Aufgaben:Exercise 2.6: Two-Way Channel

• Return to book

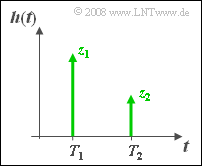
Der so genannte Zweiwegekanal wird durch folgende Impulsantwort charakterisiert (mit T₁ < T₂):

$$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( t - T_2).$$

Bis auf wenige Kombinationen der Systemparameter z₁, T₁, z₂ und T₂ wird dieser Kanal zu linearen Verzerrungen führen. Man spricht nur dann von einem verzerrungsfreien Kanal, wenn durch ihn kein einziges Eingangssignal verzerrt wird. Das bedeutet: Auch bei einem verzerrenden Kanal kann es Sonderfälle geben, bei denen tatsächlich y(t) = α · x(t – τ) gilt.

Als Testsignale werden an den Systemeingang angelegt:

• ein Diracpuls x₁(t) im Zeitabstand T₀ = 1 ms gemäß

$$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,$$

dessen Spektralfunktion ebenfalls ein Diracpuls ist, und zwar mit Abstand f₀ = 1/T₀ = 1 kHz:

$$X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k \cdot f_0) ,$$

• ein Cosinussignal mit der Frequenz f₂ = 250 Hz:

$$x_2(t) = \cos(2 \pi \cdot f_2 \cdot t) ,$$

• die Summe zweier Cosinussignale mit den Frequenzen f₂ = 250 Hz und f₃ = 1250 Hz:

$$x_3(t) = \cos(2 \pi \cdot f_2 \cdot t) + \cos(2 \pi \cdot f_3 \cdot t) .$$

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.3. Um Ihnen einige Rechnungen zu ersparen, wird folgendes Ergebnis für den Parametersatz z₁ = 1, T₁ = 0, z₂ = 0.5 und T₂ = 1 ms vorweggenommen:

$$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \hspace{0.45cm} \approx 1.118, \\ b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Der Parametersatz „z1 = 1, T1 = 0, z2 = 0” ist der einzig mögliche zur Beschreibung des idealen Kanals.
	Jeder verzerrungsfreie Kanal wird durch die beiden Kombinationen „z1 ≠ 0, z2 = 0” bzw. „z1 = 0, z2 ≠ 0 erfasst.”
	Die Werte „z1 ≠ 0” und „z2 ≠ 0” führen zu einem verzerrungsfreien Kanal, wenn T1 und T2 bestmöglich angepasst sind.

2

Es gelte z₁ = 1, T₁ = 0, z₂ = 0.5, T₂ = 1 ms. Berechnen Sie den Frequenzgang H(f) dieses Kanals. Welche Werte gibt es bei Vielfachen von 1 kHz?

$Re[H(f = n \cdot 1 \ kHz)]$ =

$Im[H(f = n \cdot 1 \ kHz)]$ =

3

Am Eingang des Systems mit gleichen Parametern wie unter c) liegt nun der Diracpuls x₁(t) an. Welche Aussagen treffen für das Ausgangssignal y₁(t) zu?

	y1(t) ist gegenüber x1(t) um eine Konstante gedämpft/verstärkt.
	y1(t) ist gegenüber x1(t) verschoben.
	y1(t) weist gegenüber x1(t) Verzerrungen auf.

4

Berechnen Sie das Signal y₂(t) als Systemantwort auf das Cosinussignal x₂(t). Welcher Signalwert tritt zum Zeitpunkt t = 0 auf?

$y_2(t = 0)$ =

5

Welche Aussagen treffen bezüglich der Signale x₃(t) und y₃(t) zu?

	y3(t) weist gegenüber x3(t) keine Verzerrungen auf.
	y3(t) weist gegenüber x3(t) Dämpfungsverzerrungen auf.
	y3(t) weist gegenüber x3(t) Phasenverzerrungen auf.

Musterlösung

Solution

1.  Mit z₁ = 1, T₁ = 0 und z₂ = 0 ist h(t) = δ(t) und dementsprechend H(f) = 1, so dass stets y(t) = x(t) gelten wird. Jede verzerrungsfreie Kanalimpulsantwort h(t) besteht aus einer einzigen Diracfunktion, zum Beispiel bei t = T₁. Dieser Fall ist im Modell durch z₂ = 0 berücksichtigt. Damit lautet der Frequenzgang:

$$H(f)= z_1\cdot {\rm e}^{-{\rm j}\cdot \hspace{0.05cm}2 \pi f T_1},$$

und es wird y(t) = z₁ · x(t – T₁) gelten. Dagegen wird der Kanal immer dann zu linearen Verzerrungen führen, wenn gleichzeitig z₁ und z₂ von 0 verschieden sind. Richtig sind demnach die Aussagen 1 und 2.

2.  Die Fouriertransformation der Impulsantwort h(t) führt auf die Gleichung:

$$H(f) = z_1\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ z_2\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2} .$$

Mit z₁ = 1, T₁ = 0, z₂ = 0.5, T₂ = 1 ms erhält man daraus:

$$H(f) =1 + 0.5 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}.$$

Aufgeschlüsselt nach Real– und Imaginärteil liefert dies:

$${\rm Re}[H(f)] = 1 + 0.5 \cdot \cos(2 \pi f \cdot 1\,{\rm ms}),\\ {\rm Im}[H(f)] = -0.5 \cdot \sin(2 \pi f \cdot 1\,{\rm ms}).$$

Bei der Frequenz f = f₁ = 1 kHz – und auch allen Vielfachen davon – ist der Realteil gleich 1.5 und der Imaginärteil verschwindet.

3.  Aus dem Ergebnis aus b) folgt weiter, dass bei allen Vielfachen von f₁ = 1 kHz der Betragsfunktion |H(f)| = 1.5 und die Phasenfunktion b(f) = 0 ist. Damit ist für diese diskreten Frequenzwerte auch die Phasenlaufzeit jeweils 0. Da aber das Spektrum X₁(f) des Diracpulses genau bei diesen Frequenzen Spektrallinien aufweist, gilt y(t) = 1.5 · x(t). Damit ist allein die erste Antwort richtig.

4.  Die Betragsfunktion lautet:

$$|H(f)| = \sqrt{{\rm Re}[H(f)]^2 + {\rm Im}[H(f)]^2} =\\ = \sqrt{1 + 0.25 \cdot \cos^2(2 \pi f \cdot T_2)+ \cos(2 \pi f \cdot T_2) + 0.25 \cdot \sin^2(2 \pi f \cdot T_2)}=\\ = \sqrt{1.25 + \cos(2 \pi f \cdot T_2) }.$$

Für die Frequenz f₂ = 0.25 kHz erhält man somit:

$$|H(f)| = \sqrt{1.25 + \cos(\frac{\pi}{2} ) }= \sqrt{1.25} = 1.118.$$

Die Phasenfunktion lautet allgemein bzw. bei der Frequenz f₂:

$$b(f) = - {\rm arctan}\hspace{0.1cm}\frac{{\rm Im}[H(f)]}{{\rm Re}[H(f)]} = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin(2 \pi f T_2)}{1+0.5 \cdot \cos(2 \pi f T_2)},$$

$$b(f = f_2) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( \pi/2)}{1+0.5 \cdot \cos(\pi/2)}={\rm arctan}\hspace{0.1cm}\frac{0.5}{1} = 0.464.$$

Damit beträgt die Phasenlaufzeit für diese Frequenz:

$$\tau_2 = \frac {b(f_2)}{2 \pi f_2} = \frac {0.464}{2 \pi \cdot 0.25\,{\rm kHz}} \approx 0.3\,{\rm ms},$$

und es gilt für das Ausgangssignal:

$$y_2(t) = 1.118 \cdot \cos(2 \pi \cdot 0.25\,{\rm kHz}\cdot (t - 0.3\,{\rm ms})).$$

Der Signalwert zum Nullzeitpunkt ist somit:

$$y_2(t=0) = 1.118 \cdot \cos(-2 \pi \cdot 0.25\,{\rm kHz} \cdot 0.3\,{\rm ms}) \approx 1.118 \cdot 0.891 \hspace{0.15cm}\underline{= 0.996}.$$

5.  Beide Frequenzen werden mit dem gleichen Dämpfungsfaktor α = 1.118 beaufschlagt; daher sind keine Dämpfungsverzerrungen festzustellen.

Mit f₃ = 1.25 kHz und T₂ = 1 ms ergibt sich für die Phasenfunktion:

$$b(f = f_3) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( 2.5 \pi)}{1+0.5 \cdot \cos(2.5 \pi)}= 0.464 = b(f = f_2),$$

also genau der gleiche Wert wie bei der Frequenz f₂ = 0.25 kHz. Trotzdem kommt es aber nun zu Phasenverzerrungen, da für f₃ die Phasenlaufzeit nur mehr τ₃ = 60 μs beträgt.

Für das Ausgangssignal kann also geschrieben werden:

$$y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot (t - 0.3\,{\rm ms}) + 1.118 \cdot \cos(2 \pi f_3 \cdot (t - 0.06\,{\rm ms}) = \\ = 1.118 \cdot \cos(2 \pi f_2 \cdot t - 27^\circ) + 1.118 \cdot \cos(2 \pi f_3 \cdot t - 27^\circ).$$

Es gibt also Phasenverzerrungen ⇒ Antwort 3, obwohl für beide Schwingungen φ₂ = φ₃ = 27° gilt. Damit keine Phasenverzerrungen auftreten, müssten die Phasenlaufzeiten τ₂ und τ₃ gleich sein und die Phasenwerte φ₂ und φ₃ linear mit den zugehörigen Frequenzen ansteigen.