Aufgaben:Exercise 3.2: Expected Value Calculations

• Return to book

Wir betrachten folgende Wahrscheinlichkeitsfunktionen:

• P_X(X) = [1/2, 1/8, 0, 3/8],

• P_Y(Y) = [1/2, 1/4, 1/4, 0],

• P_U(U) = [1/2, 1/2],

• P_V(V) = [3/4, 1/4].

Für die dazugehörigen Zufallsgrößen gelte:

• X = {0, 1, 2, 3}, Y = {0, 1, 2, 3},

• U = {0, 1}, V = {0, 1}.

Oft muss man in der Informationstheorie für solche diskreten Zufallsgrößen verschiedene Erwartungswerte der Form

$${\rm E} \left [ F(X)\right ] = \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} {\rm supp} (P_X)} \hspace{-0.1cm} P_{X}(x) \cdot F(x) $$

berechnen. Hierbei bedeuten:

• P_X(X) bezeichnet die Wahrscheinlichkeitsfunktion der diskreten Zufallsgröße X.

• Der Support von P_x umfasst alle diejenigen Realisierungen x der Zufallsgröße X mit nicht verschwindender Wahrscheinlichkeit. Formal kann hierfür geschrieben werden:

$${\rm supp} (P_X) = \{ x: \hspace{0.25cm}x \in X \hspace{0.15cm}\underline{\rm und} \hspace{0.15cm} P_X(x) \ne 0 \} \hspace{0.05cm}.$$

• F(X) ist eine (beliebige) reellwertige Funktion, die im gesamten Definitionsgebiet der Zufallsgröße angebbar ist.

In der Aufgabe sollen die Erwartungswerte für verschiedene Funktionen F(X) berechnet werden, unter anderem für

• F(X) = 1/P_X(X),

• F(X) = P_X(X),

• F(X) = –log₂ P_X(X).

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 3.1 dieses Buches. Weiter gilt, ohne dass dies für die Lösung dieser Aufgabe von Interesse ist:

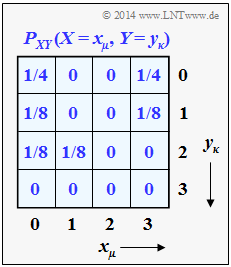
• Die beiden „eindimensionalen” Wahrscheinlichkeitsfunktionen P_X(X) und P_Y(Y) ergeben sich aus der dargestellten 2D–PMF P_XY(X, Y), wie in Aufgabe Z3.2 gezeigt werden soll.

• Zu den binären Wahrscheinlichkeitsfunktionen P_U(U) und P_V(V) kommt man entsprechend den Modulo–Operationen U = X mod 2 sowie V = Y mod 2 (siehe ebenfalls Aufgabe Z3.2)

Fragebogen

1

Welche Ergebnisse liefern die folgenden Erwartungswerte?

$E[1/P_X(X)]$ =

$E[1/P_Y(Y)]$ =

2

Geben Sie die folgenden Erwartungswerte an:

$E[P_X(X)]$ =

$E[P_Y(Y)]$ =

3

Berechnen Sie nun die folgenden Erwartungswerte:

$E[P_Y(X)]$ =

$E[P_X(Y)]$ =

4

Welche der folgenden Aussagen sind zutreffend?

	E[–log2 PU(U)] ergibt die Entropie der Zufallsgröße U.
	E[–log2 PV(V)] ergibt die Entropie der Zufallsgröße V.
	E[–log2 PV(U)] ergibt die Entropie der Zufallsgröße V.

Musterlösung

Solution

1.  Allgemein gilt für den Erwartungswert der Funktion F(X) hinsichtlich der Zufallsvariablen X:

$${\rm E} \left [ F(X)\right ] = \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} {\rm supp} (P_X)} \hspace{0.01cm} P_{X}(x) \cdot F(x) \hspace{0.05cm}.$$

Im vorliegenden Beispiel gilt X = {0, 1, 2, 3} und P_X(X) = [1/2, 1/8, 0, 3/8]. Wegen P_X(X = 2) = 0 ergibt sich somit für die zu berücksichtigende Menge („Support”) in obiger Summation:

$${\rm supp} (P_X) = \{ 0\hspace{0.05cm}, 1\hspace{0.05cm}, 3 \} \hspace{0.05cm}.$$

Mit F(X) = 1/P_X(X) erhält man weiter:

$${\rm E} \left [ 1/P_X(X)\right ] = \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{0.01cm} P_{X}(x) \cdot {1}/{P_X(x)} = \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} 1 \hspace{0.15cm}\underline{ = 3} \hspace{0.05cm}.$$

Der zweite Erwartungswert liefert mit supp(P_Y) = {0, 1, 2} das gleiche Ergebnis: E[1/P_Y(Y)] = 3.

2.  In beiden Fällen ist der Index der Wahrscheinlichkeitsfunktion mit der Zufallsvariablen (X bzw. Y) identisch und man erhält

$${\rm E} \left [ P_X(X)\right ] = \hspace{0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{0.3cm} P_{X}(x) \cdot {P_X(x)} = (1/2)^2 + (1/8)^2 + (3/8)^2 = 13/32 \hspace{0.15cm}\underline{ \approx 0.406} \hspace{0.05cm},$$

$${\rm E} \left [ P_Y(Y)\right ] = \hspace{0.3cm} \sum_{y \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 2 \}} \hspace{0.3cm} P_Y(y) \cdot P_Y(y) = (1/2)^2 + (1/4)^2 + (1/4)^2 \hspace{0.15cm}\underline{ = 0.375} \hspace{0.05cm}.$$

3.  Hier gelten folgende Gleichungen:

$${\rm E} \left [ P_Y(X)\right ] = \hspace{0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{0.3cm} P_{X}(x) \cdot {P_Y(x)} = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{8} \cdot \frac{1}{4} + \frac{3}{8} \cdot 0 = 9/32 \hspace{0.15cm}\underline{ \approx 0.281} \hspace{0.05cm},$$

Die Erwartungswertbildung bezieht sich hier auf P_X(·), also auf die Zufallsgröße X. P_Y(·) ist dabei die formale Funktion ohne (direkten) Bezug zur Zufallsgröße Y.

Für den zweiten Erwartungswert erhält man den gleichen Zahlenwert (das muss nicht so sein):

$${\rm E} \left [ P_X(Y)\right ] = \hspace{0.3cm} \sum_{y \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 2 \}} \hspace{0.3cm} P_{Y}(y) \cdot {P_X(y)} = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{8} + \frac{1}{4} \cdot 0 = 9/32 \hspace{0.15cm}\underline{ \approx 0.281} \hspace{0.05cm}.$$

4.  Wir berechnen zunächst die drei Erwartungswerte:

$${\rm E} \left [-{\rm log}_2 \hspace{0.1cm} P_U(U)\right ] = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{1} + \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{1} \hspace{0.15cm}\underline{ = 1\,{\rm bit}} \hspace{0.05cm},$$

$${\rm E} \left [-{\rm log}_2 \hspace{0.1cm} P_V(V)\right ] = \frac{3}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{3} + \frac{1}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{1} \hspace{0.15cm}\underline{ = 0.811\,{\rm bit}} \hspace{0.05cm},$$

$${\rm E} \left [-{\rm log}_2 \hspace{0.1cm} P_V(U)\right ] = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{3} + \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{1} \hspace{0.15cm}\underline{ = 1.208\,{\rm bit}} \hspace{0.05cm}.$$

Richtig sind demnach die beiden ersten Aussagen:

• Die Entropie H(U) = 1 bit kann entsprechend der ersten Gleichung berechnet werden. Sie gilt für die binäre Zufallsgröße U mit gleichen Wahrscheinlichkeiten.

• Die Entropie H(V) = 0.811 bit berechnet sich entsprechend der zweiten Gleichung. Aufgrund der Wahrscheinlichkeiten 3/4 und 1/4 ist die Entropie (Unsicherheit) kleiner als für die Zufallsgröße U.

• Der dritte Erwartungswert kann schon allein vom Ergebnis her (1.208 bit) nicht die Entropie einer binären Zufallsgröße angeben, die stets auf 1 bit begrenzt ist.