Difference between revisions of "Aufgaben:Exercise 3.10: Mutual Information at the BSC"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Anwendung auf die Digitalsignalübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multi…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2787__Inf_A_3_9.png|right|]] |
| + | Wir betrachten den $Binary$ $Symmetric$ $Channel$ (BSC). Für die gesamte Aufgabe gelten die Parameterwerte: | ||
| + | :* Verfälschungswahrscheinlichkeit: $\epsilon = 0.1$ | ||
| + | :* Wahrscheinlichkeit für $0$: $p_0 = 0.2$, | ||
| + | :* Wahrscheinlichkeit für $1$: $p_1 = 0.8$. | ||
| + | |||
| + | Damit lautet die Wahrscheinlichkeitsfunktion der Quelle: | ||
| + | |||
| + | $P_X(X)= (0.2 , 0.8)$ | ||
| + | |||
| + | und für die Quellenentropie gilt: | ||
| + | |||
| + | $H(X) = p_0 . log_2 \frac{1}{p_0} + p_1 . log_2 \frac{1}{p_1} = H_{bin}(0.2) = 0.7219 (bit)$ | ||
| + | |||
| + | In der Aufgabe sollen ermittelt werden: | ||
| + | :* die Wahrscheinlichkeitsfunktion der Sinke: | ||
| + | |||
| + | $P_Y(Y) = (P_Y(0) , P_Y(1))$, | ||
| + | :* die Verbundwahrscheinlichkeitsfunktion : | ||
| + | $P_{XY}(X, Y) = \begin{pmatrix} p_{00} & p_{01}\\ p_{10} & p_{11} \end{pmatrix} \hspace{0.05cm}$ | ||
| + | :* die Transinformation | ||
| + | |||
| + | $I(X;Y) = E[ log_2 \frac{P_{ XY }(X,Y)}{P_X(X) . P_Y(Y)}]$, | ||
| + | :*die Äquivokation: | ||
| + | |||
| + | $H(X \mid Y) = E[log_2 \frac{1}{P_{ X \mid Y }(X \mid Y)}]$, | ||
| + | :*die Irrelevanz: | ||
| + | |||
| + | $H(Y \mid X) = E[log_2 \frac{1}{P_{ Y \mid X }(Y \mid X)}]$ | ||
| + | |||
| + | '''Hinwies:''' Die Aufgabe gehört zu [http://en.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3.] In der Aufgabe Z3.9 wird die [http://en.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung#Kanalkapazit.C3.A4t_eines_Bin.C3.A4rkanals Kanalkapazität] $C_{ BSC }$ des $BSC$–Modells berechnet. Diese ergibt sich als die maximale Transinformation $I(X; Y)$ durch Maximierung bezüglich der Symbolwahrscheinlichkeiten $p_0$ bzw. $p_1 = 1 – p_0$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Revision as of 22:09, 26 November 2016
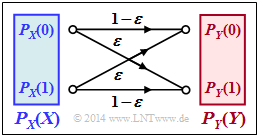
Wir betrachten den $Binary$ $Symmetric$ $Channel$ (BSC). Für die gesamte Aufgabe gelten die Parameterwerte:
- Verfälschungswahrscheinlichkeit: $\epsilon = 0.1$
- Wahrscheinlichkeit für $0$: $p_0 = 0.2$,
- Wahrscheinlichkeit für $1$: $p_1 = 0.8$.
Damit lautet die Wahrscheinlichkeitsfunktion der Quelle:
$P_X(X)= (0.2 , 0.8)$
und für die Quellenentropie gilt:
$H(X) = p_0 . log_2 \frac{1}{p_0} + p_1 . log_2 \frac{1}{p_1} = H_{bin}(0.2) = 0.7219 (bit)$
In der Aufgabe sollen ermittelt werden:
- die Wahrscheinlichkeitsfunktion der Sinke:
$P_Y(Y) = (P_Y(0) , P_Y(1))$,
- die Verbundwahrscheinlichkeitsfunktion :
$P_{XY}(X, Y) = \begin{pmatrix} p_{00} & p_{01}\\ p_{10} & p_{11} \end{pmatrix} \hspace{0.05cm}$
- die Transinformation
$I(X;Y) = E[ log_2 \frac{P_{ XY }(X,Y)}{P_X(X) . P_Y(Y)}]$,
- die Äquivokation:
$H(X \mid Y) = E[log_2 \frac{1}{P_{ X \mid Y }(X \mid Y)}]$,
- die Irrelevanz:
$H(Y \mid X) = E[log_2 \frac{1}{P_{ Y \mid X }(Y \mid X)}]$
Hinwies: Die Aufgabe gehört zu Kapitel 3.3. In der Aufgabe Z3.9 wird die Kanalkapazität $C_{ BSC }$ des $BSC$–Modells berechnet. Diese ergibt sich als die maximale Transinformation $I(X; Y)$ durch Maximierung bezüglich der Symbolwahrscheinlichkeiten $p_0$ bzw. $p_1 = 1 – p_0$.
Fragebogen
Musterlösung