Difference between revisions of "Digital Signal Transmission/Linear Nyquist Equalization"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Impulsinterferenzen und Entzerrungsverfahren |Vorherige Seite=Impulsinterferenzen bei mehrstufiger Übertragung |Nächste Seite=Entschei…“) |
|||
| Line 44: | Line 44: | ||
*Wir bezeichnen die Konfiguration als Optimale Nyquistentzerrung (ONE). Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst <i>M</i> = 2.<br><br> | *Wir bezeichnen die Konfiguration als Optimale Nyquistentzerrung (ONE). Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst <i>M</i> = 2.<br><br> | ||
| + | == Wirkungsweise des Transversalfilters (1) == | ||
| + | <br> | ||
| + | Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters | ||
| + | :<math>H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ | ||
| + | \hspace{0.4cm} | ||
| + | h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) | ||
| + | \hspace{0.05cm}.</math> | ||
| + | <i>N</i> gibt die Ordnung des Filters an. Für die Filterkoeffizienten gilt <i>k</i><sub>–λ</sub> = <i>k</i><sub>λ</sub>. Dieses Filter ist somit durch die Koeffizienten <i>k</i><sub>0</sub>, ... , <i>k<sub>N</sub></i> vollständig bestimmt. Die Grafik zeigt ein Filter zweiter Ordnung (<i>N</i> = 2).<br> | ||
| + | |||
| + | [[File:P ID1424 Dig T 3 5 S2 version2.png|Transversalfilter als Teil des optimalen Nyquistentzerrers|class=fit]]<br> | ||
| + | |||
| + | Für den Eingangsimpuls <i>g<sub>m</sub></i>(<i>t</i>) setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser | ||
| + | |||
| + | *symmetrisch um <i>t</i> = 0 ist (Ausgang des Matched–Filters),<br> | ||
| + | *zu den Zeiten <i>ν</i><i>T</i> und –<i>ν</i><i>T</i> den Wert <i>g<sub>m</sub></i>(<i>ν</i>) besitzt.<br><br> | ||
| + | |||
| + | Damit sind die Eingangsimpulswerte: | ||
| + | |||
| + | :<math>...\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace | ||
| + | {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} | ||
| + | ... \hspace{0.05cm}.</math> | ||
| + | |||
| + | Für den Detektionsgrundimpuls <i>g<sub>d</sub></i>(<i>t</i>) am Filterausgang ergeben sich demzufolge zu den Zeitpunkten <i>ν</i><i>T</i> mit den Abkürzungen <i>g</i><sub>0</sub> = <i>g<sub>d</sub></i>(<i>t</i> = 0), <i>g</i><sub>1</sub> = <i>g<sub>d</sub></i>(<i>t</i> = ±<i>T</i>), <i>g</i><sub>2</sub> = <i>g<sub>d</sub></i>(<i>t</i> = ±2<i>T</i>) folgende Werte: | ||
| + | |||
| + | :<math>t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 | ||
| + | \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm}</math> | ||
| + | :<math>t = \pm T\hspace{-0.1cm}:\hspace{0.2cm}g_1 = k_0 \cdot g_m(1) + k_1 | ||
| + | \cdot [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3)],</math> | ||
| + | :<math>t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 | ||
| + | \cdot [g_m(1)+g_m(3)]+ k_2 \cdot [g_m(2)+g_m(4)] | ||
| + | \hspace{0.05cm}.</math> | ||
| + | |||
| + | Aus diesem System mit drei linear unabhängigen Gleichungen kann man nun die Filterkoeffizienten <i>k</i><sub>0</sub>, <i>k</i><sub>1</sub> und <i>k</i><sub>2</sub> so bestimmen, dass der Detektionsgrundimpuls <i>g<sub>d</sub></i>(<i>t</i>) durch die normierten Stützstellen | ||
| + | |||
| + | :<math>...\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 | ||
| + | ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 | ||
| + | = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} ...</math> | ||
| + | |||
| + | vollständig gegeben ist. Auf der nächsten Seite wird die Optimierung der Filterkoeffizienten an einem einfachen Beispiel verdeutlicht.<br> | ||
Revision as of 21:43, 26 December 2016
Struktur des optimalen Nyquistentzerrers
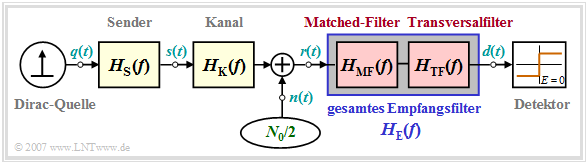
In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems aus.
Hierzu ist anzumerken:
- Die Diracquelle liefert die zu übertragende Nachricht (Amplitudenkoeffizienten aν) in binärer bipolarer Form. Sie wird als redundanzfrei vorausgesetzt.
- Die Sendeimpulsform gs(t) wird durch den Senderfrequenzgang HS(f) berücksichtigt. Bei allen Beispielen ist HS(f) = si(π f T) zugrunde gelegt.
- Bei manchen Herleitungen werden Sender und Kanal – hierfür wird meist ein Koaxialkabel angenommen – durch den gemeinsamen Frequenzgang HSK(f) = HS(f) · HK(f) zusammengefasst.
- Das Empfangsfilter HE(f) setzt sich multiplikativ aus dem Matched–Filter HMF(f) = HSK∗(f) und dem Transversalfilter HTF(f) zusammen, zumindest kann es gedanklich so aufgespalten werden.
- Der Gesamtfrequenzgang zwischen der Diracquelle und dem Schwellenwertentscheider soll die erste Nyquistbedingung erfüllen. Es muss also gelten:
- \[H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) = H_{\rm Nyq}(f) \hspace{0.05cm}.\]
- Mit dieser Bedingung ergibt sich die maximale Augenöffnung (keine Impulsinterferenzen). Deshalb gelten für das Detektions–SNR und den Systemwirkungsgrad bei binärer Signalisierung:
- \[\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.05cm}.\]
- Die Optimierungsaufgabe beschränkt sich also darauf, das Empfangsfilter HE(f) so zu bestimmen, dass die normierte Rauschleistung vor dem Entscheider den kleinstmöglichen Wert annimmt:
- \[\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \stackrel {!}{=} {\rm Minimum}\hspace{0.05cm}.\]
- Wir bezeichnen die Konfiguration als Optimale Nyquistentzerrung (ONE). Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst M = 2.
Wirkungsweise des Transversalfilters (1)
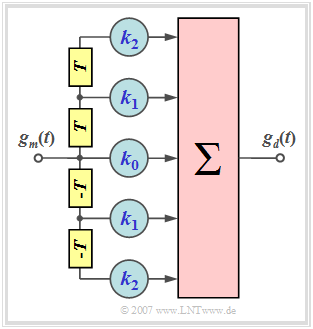
Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters
\[H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) \hspace{0.05cm}.\]
N gibt die Ordnung des Filters an. Für die Filterkoeffizienten gilt k–λ = kλ. Dieses Filter ist somit durch die Koeffizienten k0, ... , kN vollständig bestimmt. Die Grafik zeigt ein Filter zweiter Ordnung (N = 2).
Für den Eingangsimpuls gm(t) setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser
- symmetrisch um t = 0 ist (Ausgang des Matched–Filters),
- zu den Zeiten νT und –νT den Wert gm(ν) besitzt.
Damit sind die Eingangsimpulswerte:
\[...\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} ... \hspace{0.05cm}.\]
Für den Detektionsgrundimpuls gd(t) am Filterausgang ergeben sich demzufolge zu den Zeitpunkten νT mit den Abkürzungen g0 = gd(t = 0), g1 = gd(t = ±T), g2 = gd(t = ±2T) folgende Werte:
\[t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm}\] \[t = \pm T\hspace{-0.1cm}:\hspace{0.2cm}g_1 = k_0 \cdot g_m(1) + k_1 \cdot [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3)],\] \[t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 \cdot [g_m(1)+g_m(3)]+ k_2 \cdot [g_m(2)+g_m(4)] \hspace{0.05cm}.\]
Aus diesem System mit drei linear unabhängigen Gleichungen kann man nun die Filterkoeffizienten k0, k1 und k2 so bestimmen, dass der Detektionsgrundimpuls gd(t) durch die normierten Stützstellen
\[...\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} ...\]
vollständig gegeben ist. Auf der nächsten Seite wird die Optimierung der Filterkoeffizienten an einem einfachen Beispiel verdeutlicht.