Difference between revisions of "Digital Signal Transmission/Linear Nyquist Equalization"
| Line 165: | Line 165: | ||
== Beschreibung im Frequenzbereich (2) == | == Beschreibung im Frequenzbereich (2) == | ||
<br> | <br> | ||
| − | Die linke Grafik zeigt den Verlauf 20 · lg <i>H</i><sub>TF</sub>(<i>f</i>) im Bereich | <i>f</i> | ≤ 1/<i>T</i>. Rechts ist der Frequenzgang | + | Die linke Grafik zeigt den Verlauf 20 · lg <i>H</i><sub>TF</sub>(<i>f</i>) im Bereich | <i>f</i> | ≤ 1/<i>T</i>. Rechts ist der Frequenzgang 20 · lg |<i>H</i><sub>E</sub>(<i>f</i>)| des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt: |
:<math>H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{^\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | :<math>H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{^\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
| Line 183: | Line 183: | ||
\approx 80\,{\rm dB}\hspace{0.05cm}.</math> | \approx 80\,{\rm dB}\hspace{0.05cm}.</math> | ||
| − | Für <i>a</i><sub>∗</sub> = 0 dB (idealer Kanal) kann auf das Transversalfilter verzichtet werden und es gilt, wie bereits im Kapitel 1.2 hergeleitet: | + | Für <i>a</i><sub>∗</sub> = 0 dB (idealer Kanal) kann auf das Transversalfilter verzichtet werden und es gilt, wie bereits im [http://en.lntwww.de/Digitalsignal%C3%BCbertragung/Fehlerwahrscheinlichkeit_bei_Basisband%C3%BCbertragung#Optimaler_Bin.C3.A4rempf.C3.A4nger_-_Realisierung_mit_Matched-Filter_.281.29 Kapitel 1.2] hergeleitet: |
:<math>H_{\rm E}(f) =H_{\rm S}(f) = {\rm si} (\pi f T)\hspace{0.05cm}.</math> | :<math>H_{\rm E}(f) =H_{\rm S}(f) = {\rm si} (\pi f T)\hspace{0.05cm}.</math> | ||
Revision as of 23:49, 26 December 2016
Contents
Struktur des optimalen Nyquistentzerrers
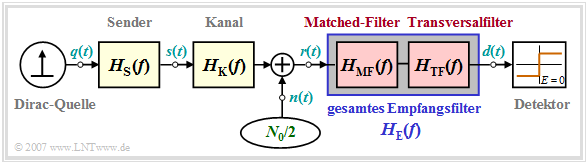
In diesem Abschnitt gehen wir von folgendem Blockschaltbild eines Binärsystems aus.
Hierzu ist anzumerken:
- Die Diracquelle liefert die zu übertragende Nachricht (Amplitudenkoeffizienten aν) in binärer bipolarer Form. Sie wird als redundanzfrei vorausgesetzt.
- Die Sendeimpulsform gs(t) wird durch den Senderfrequenzgang HS(f) berücksichtigt. Bei allen Beispielen ist HS(f) = si(π f T) zugrunde gelegt.
- Bei manchen Herleitungen werden Sender und Kanal – hierfür wird meist ein Koaxialkabel angenommen – durch den gemeinsamen Frequenzgang HSK(f) = HS(f) · HK(f) zusammengefasst.
- Das Empfangsfilter HE(f) setzt sich multiplikativ aus dem Matched–Filter HMF(f) = HSK∗(f) und dem Transversalfilter HTF(f) zusammen, zumindest kann es gedanklich so aufgespalten werden.
- Der Gesamtfrequenzgang zwischen der Diracquelle und dem Schwellenwertentscheider soll die erste Nyquistbedingung erfüllen. Es muss also gelten:
- \[H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm MF}(f) \cdot H_{\rm TF}(f) = H_{\rm Nyq}(f) \hspace{0.05cm}.\]
- Mit dieser Bedingung ergibt sich die maximale Augenöffnung (keine Impulsinterferenzen). Deshalb gelten für das Detektions–SNR und den Systemwirkungsgrad bei binärer Signalisierung:
- \[\rho_d = \frac{2 \cdot s_0^2 \cdot T}{\sigma_d^2} = \frac{2 \cdot s_0^2 \cdot T}{N_0}\cdot \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = \frac{\rho_d }{\rho_{d,\hspace{0.05cm} {\rm max}}} = \frac{\rho_d }{2 \cdot s_0^2 \cdot T/N_0} = \frac{1}{\sigma_{d,\hspace{0.05cm} {\rm norm}}^2} \hspace{0.05cm}.\]
- Die Optimierungsaufgabe beschränkt sich also darauf, das Empfangsfilter HE(f) so zu bestimmen, dass die normierte Rauschleistung vor dem Entscheider den kleinstmöglichen Wert annimmt:
- \[\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = \frac{\sigma_d^2}{N_0/ T} =T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \stackrel {!}{=} {\rm Minimum}\hspace{0.05cm}.\]
- Wir bezeichnen die Konfiguration als Optimale Nyquistentzerrung (ONE). Obwohl diese auch – und besonders effektiv – bei Mehrstufensystemen anwendbar ist, setzen wir zunächst M = 2.
Wirkungsweise des Transversalfilters (1)
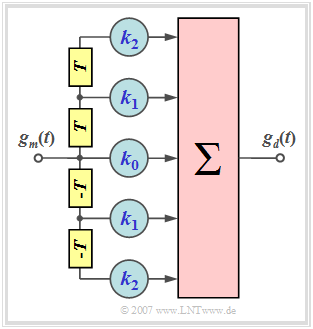
Verdeutlichen wir uns zunächst die Aufgabe des symmetrischen Transversalfilters
\[H_{\rm TF}(f) \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} h_{\rm TF}(t) = \sum_{\lambda = -N}^{+N} k_\lambda \cdot \delta(t - \lambda \cdot T) \hspace{0.05cm}.\]
N gibt die Ordnung des Filters an. Für die Filterkoeffizienten gilt k–λ = kλ. Dieses Filter ist somit durch die Koeffizienten k0, ... , kN vollständig bestimmt. Die Grafik zeigt ein Filter zweiter Ordnung (N = 2).
Für den Eingangsimpuls gm(t) setzen wir ohne Einschränkung der Allgemeingültigkeit voraus, dass dieser
- symmetrisch um t = 0 ist (Ausgang des Matched–Filters),
- zu den Zeiten νT und –νT den Wert gm(ν) besitzt.
Damit sind die Eingangsimpulswerte:
\[...\hspace{0.2cm} , g_m(3),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(1),\hspace{0.15cm}\hspace {0.15cm}g_m(0),\hspace{0.15cm}g_m(1),\hspace{0.15cm}g_m(2),\hspace{0.15cm}g_m(3),\hspace{0.1cm} ... \hspace{0.05cm}.\]
Für den Detektionsgrundimpuls gd(t) am Filterausgang ergeben sich demzufolge zu den Zeitpunkten νT mit den Abkürzungen g0 = gd(t = 0), g1 = gd(t = ±T), g2 = gd(t = ±2T) folgende Werte:
\[ t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 = k_0 \cdot g_m(0) + k_1 \cdot 2 \cdot g_m(1) \hspace{1.23cm}+k_2 \cdot 2 \cdot g_m(2),\hspace{0.05cm} \] \[ t = \pm T\hspace{-0.1cm}:\hspace{0.2cm}g_1 = k_0 \cdot g_m(1) + k_1 \cdot [g_m(0)+g_m(2)]+ k_2 \cdot [g_m(1)+g_m(3)], \] \[ t = \pm 2T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot g_m(2) + k_1 \cdot [g_m(1)+g_m(3)]+ k_2 \cdot [g_m(2)+g_m(4)] \hspace{0.05cm}. \]
Aus diesem System mit drei linear unabhängigen Gleichungen kann man nun die Filterkoeffizienten k0, k1 und k2 so bestimmen, dass der Detektionsgrundimpuls gd(t) durch die normierten Stützstellen
\[...\hspace{0.15cm} , g_3,\hspace{0.25cm}g_2 = 0 ,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_0 = 1,\hspace{0.15cm}g_1 = 0 ,\hspace{0.15cm}g_2 = 0 ,\hspace{0.25cm}g_3 ,\hspace{0.15cm} ...\]
vollständig gegeben ist. Auf der nächsten Seite wird die Optimierung der Filterkoeffizienten an einem einfachen Beispiel verdeutlicht.
Wirkungsweise des Transversalfilters (2)
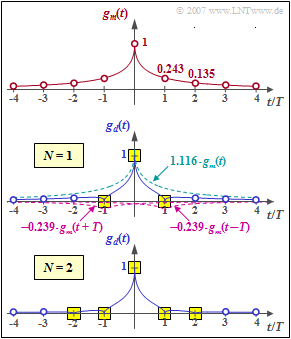
\[g_m(t) = {\rm exp }\left ( - \sqrt{2 \cdot |t|/T}\right )\]
\[\Rightarrow \hspace{0.3cm} g_m(0) = 1 ,\hspace{0.15cm}g_m(1)= 0.243,\hspace{0.15cm}g_m(2)= 0.135,\hspace{0.15cm}g_m(3)= 0.086, \hspace{0.15cm}g_m(4)= 0.059 \hspace{0.05cm}.\]
Für den Ausgangsimpuls soll gd(0) = 1 und gd(±T) = 0 gelten. Hierzu eignet sich ein Laufzeitfilter erster Ordnung mit den Koeffizienten k0 und k1, die folgende Bedingungen erfüllen müssen:
\[t = \pm T\hspace{-0.1cm} : \hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot [1.000 +0.135] = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{k_1} = -0.214 \cdot {k_0}\hspace{0.05cm},\] \[ t = 0 \hspace{-0.1cm} : \hspace{0.2cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243= 1\hspace{0.3cm}\Rightarrow \hspace{0.3cm}0.896 \cdot {k_0} = 1 \hspace{0.05cm}.\]
Daraus erhält man die optimalen Filterkoeffizienten k0 = 1.116 und k1 = 0.239. Das mittlere Diagramm zeigt, dass damit der erste Vorläufer und der erste Nachläufer kompensiert werden können und zugleich gd(0) = 1 gilt (gelbe Hinterlegung). Die weiteren Detektionsgrundimpulswerte (blaue Kreise) sind aber von 0 verschieden und bewirken Impulsinterferenzen.
Das untere Diagramm zeigt, dass mit einem Filter zweiter Ordnung (N = 2) Nulldurchgänge bei ±T und bei ±2T erzwungen werden, wenn die Koeffizienten k0 = 1.127, k1 = 0.219 und k2 = 0.075 geeignet gewählt sind. Das Gleichungssystem zur Bestimmung der optimalen Koeffizienten lautet dabei:
\[t = 0\hspace{-0.1cm}:\hspace{0.2cm}g_0 = k_0 \cdot 1.000 + k_1 \cdot 2 \cdot 0.243 + k_2 \cdot 2 \cdot 0.135 = 1\hspace{0.05cm},\\ t= \pm T\hspace{-0.1cm}:\hspace{0.2cm}g_1 = k_0 \cdot 0.243 + k_1 \cdot [1.000+0.135]+ k_2 \cdot [0.243+0.086] = 0\hspace{0.05cm}, \\ t = \pm 2 T\hspace{-0.1cm}:\hspace{0.2cm}g_2 = k_0 \cdot 0.135 + k_1 \cdot [0.243+0.086]+ k_2 \cdot [1.000 + 0.059]= 0 \hspace{0.05cm}.\]
Die Ergebnisse können wie folgt verallgemeinert werden:
- Mit einem Laufzeitfilter N–ter Ordnung können der Hauptwert gd(0) zu 1 (normiert) sowie die ersten N Nachläufer und die ersten N Vorläufer zu Null gemacht werden.
- Weitere Vor– und Nachläufer (|ν| > N) lassen sich so nicht kompensieren. Es ist auch möglich, dass diese außerhalb des Kompensationsbereichs vergrößert werden oder sogar neu entstehen.
- Im Grenzübergang N → ∞ (in der Praxis heißt das: ein Filter mit sehr vielen Koeffizienten) ist eine vollständige Nyquistentzerrung und damit eine impulsinterferenzfreie Übertragung möglich.
Beschreibung im Frequenzbereich (1)
Die Tatsache, dass sich der optimale Nyquistentzerrer multiplikativ aus
- dem Matched–Filter HMF(f) = HS∗(f) · HK∗(f) – also angepasst an den Empfangsgrundimpuls –
- und einem Transversalfilter HTF(f) mit unendlich vielen Filterkoeffizienten
zusammensetzt, folgt aus dem ersten Nyquistkriterium. Durch Anwendung der Variationsrechnung erhält man den Frequenzgang des Transversalfilters (siehe Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.):
\[H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2} \hspace{0.3cm}{\rm{mit}}\hspace{0.3cm}H_{\rm SK}(f) = H_{\rm S}(f)\cdot H_{\rm K}(f) \hspace{0.05cm}.\]
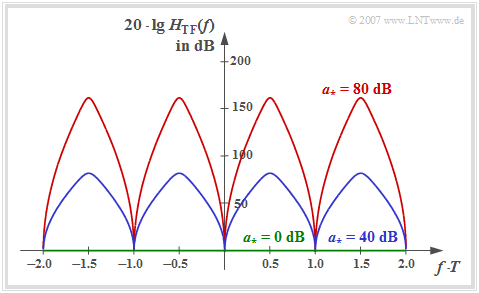
Die Grafik zeigt diesen Verlauf in logarithmierter Form für rechteckförmige NRZ–Sendeimpulse und ein Koaxialkabel mit der charakteristischen Kabeldämpfung
- a∗ = 0 dB ⇒ grüne Null–Linie,
- a∗ = 40 dB ⇒ blauer Funktionsverlauf,
- a∗ = 80 dB ⇒ roter Funktionsverlauf.
Man erkennt aus obiger Gleichung und dieser Skizze:
- HTF(f) ist reell, woraus sich die symmetrische Struktur des Transversalfilters ergibt: k–λ = kλ.
- HTF(f) ist eine mit der Frequenz 1/T periodische Funktion.
- Die Koeffizienten ergeben sich somit aus der Fourierreihe (angewandt auf die Spektralfunktion):
- \[k_\lambda =T \cdot \int_{-1/(2T)}^{+1/(2T)}\frac{\cos(2 \pi f \lambda T)} {\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2} \hspace{0.2cm} {\rm d} f \hspace{0.25cm}\Rightarrow \hspace{0.25cm}H_{\rm TF}(f) = \sum\limits_{\lambda = -\infty}^{+\infty} k_\lambda \cdot {\rm e}^{-{\rm j}2 \pi f \lambda T}\hspace{0.05cm}.\]
Die Bildbeschreibung wird auf der nächsten Seite fortgesetzt.
Beschreibung im Frequenzbereich (2)
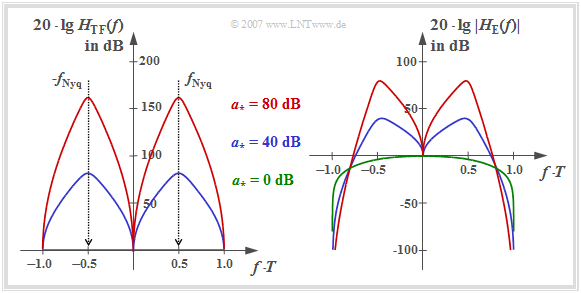
Die linke Grafik zeigt den Verlauf 20 · lg HTF(f) im Bereich | f | ≤ 1/T. Rechts ist der Frequenzgang 20 · lg |HE(f)| des gesamten Empfangsfilters einschließlich Matched–Filter dargestellt. Es gilt:
\[H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f) = \frac{H_{\rm SK}^{^\star}(f)}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}.\]
Zu diesen Darstellungen ist anzumerken:
- Der Transversalfilter–Frequenzgang HTF(f) ist symmetrisch zur Nyquistfrequenz fNyq = 1/(2T). Diese Symmetrie ist beim Empfangsfilter–Gesamtfrequenzgang HE(f) nicht mehr gegeben.
- Die Maxima der Frequenzgänge HTF(f) und |HE(f)| hängen signifikant von der charakteristischen Kabeldämpfung ab. Es gilt:
- \[a_{\star} = 40\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}[H_{\rm TF}(f)]\hspace{0.1cm} \approx 80\,{\rm dB}, \hspace{0.2cm}{\rm Max}[|H_{\rm E}(f)|] \approx 40\,{\rm dB}\hspace{0.05cm},\]
- \[a_{\star} = 80\,{\rm dB}\hspace{-0.1cm}:\hspace{0.2cm}{\rm Max}[H_{\rm TF}(f)] \approx 160\,{\rm dB}, \hspace{0.2cm}{\rm Max}[|H_{\rm E}(f)|] \approx 80\,{\rm dB}\hspace{0.05cm}.\]
Für a∗ = 0 dB (idealer Kanal) kann auf das Transversalfilter verzichtet werden und es gilt, wie bereits im Kapitel 1.2 hergeleitet:
\[H_{\rm E}(f) =H_{\rm S}(f) = {\rm si} (\pi f T)\hspace{0.05cm}.\]