Aufgaben:Exercise 2.2: Modulation Depth

• Return to book

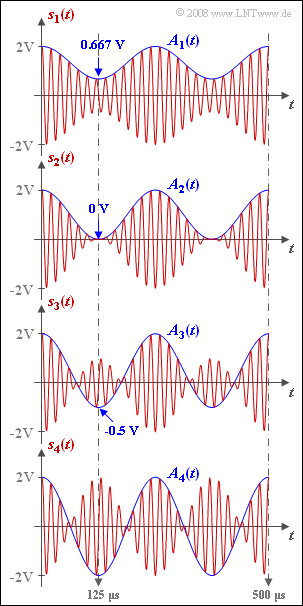
Die Grafik zeigt ZSB–amplitudenmodulierte Signale $s_1(t)$ bis $s_4(t)$ mit unterschiedlichem Modulationsgrad. Das Nachrichtensignal $q(t)$ und das Trägersignal $z(t)$ seien jeweils cosinusförmig: $$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$ $$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$ Das modulierte Signal (Sendesignal) lautet somit mit dem im Modulator zugesetzten Gleichanteil $A_T$: $$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$ Ist der Modulationsgrad m ≤ 1, so ist A(t) gleich der Hüllkurve a(t). Dagegen gilt für m > 1: $$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$ Der cosinusförmige Verlauf $A(t)$ schwankt zwischen $A_{max}$ und $A_{min}$, wobei wegen der obigen Normierung stets $A_{max} = 2V$ ist. Die Minimalwerte von $A(t)$ treten zum Beispiel bei der halben Periodendauer des Quellensignals (also für $t = 125 μs$) auf: $$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$ Die Zahlenwerte sind in der Grafik angegeben.

Hinweis:Die Aufgabe bezieht sich auf den Theoriteil von Kapitel 2.1.

Fragebogen

1

Bestimmen Sie für die Signale $s_1(t)$, $s_2(t)$, $s_3(t)$ jeweils den Modulationsgrad.

$m_1$ =

$m_2$ =

$m_3$ =

2

Welche Aussagen treffen für das Signal $s_4(t)$ zu?

	Es handelt sich um „ZSB–AM ohne Träger”.
	Der Modulationsgrad ist $m = 0$.
	Der Modulationsgrad ist unendlich groß.

3

Es gelte nun $A_T = A_N = 1 V$, also $m = 1$. Wie lautet das Spektrum $S_+(f)$ des analytischen Signals? Welche Diracgewichte treten bei $f_T$ sowie bei $f_T$ $± f_N$ auf?

$S_+(f_T)$ = $\text{V}$

$S_+(f_T ± f_N)$ = $\text{V}$

4

Welcher Anteil $P_T/P_S$ der gesamten Sendeleistung $P_S$ geht allein auf den Träger zurück, der nicht zur Demodulation genutzt werden kann?

$m = 1: P_T/P_S$ =

5

Verallgemeinern Sie das Ergebnis aus d) für einen beliebigen Modulationsgrad. Welche Leistungsverhältnisse ergeben sich für $m = 0.5$, $m = 3$ und $m → ∞$ ?

$m = 0.5 : P_T/P_S$ =

$m = 3.0 : P_T/P_S$ =

$m → ∞ : P_T/P_S$ =

6

Welche der nachfolgenden Bewertungen erscheinen Ihnen nach den bisherigen Berechnungen als sinnvoll?

	m ≈ 1 ist aus energetischen Gründen günstiger als ein kleines m.
	Nur bei Hüllkurvendemodulation ist der Träger sinnvoll.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.