Aufgaben:Exercise 2.3Z: DSB-AM due to Nonlinearity

• Return to book

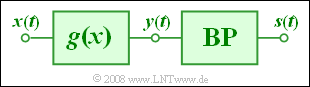
In dieser Aufgabe betrachten wir die Realisierung einer Zweiseitenband–Amplitudenmodulation mittels der nichtlinearen Kennlinie $$y = g(x) = c_1 \cdot x + c_2 \cdot x^2+ c_3 \cdot x^3\hspace{0.05cm}$$ $$ \Rightarrow c_1 = 2,\hspace{0.2cm}c_2 = 0.25/{\rm V},\hspace{0.2cm}c_3 = 0 \hspace{0.1cm}{\rm bzw.}\hspace{0.1cm}c_3 = 0.01/{\rm V^2}\hspace{0.05cm}.$$ Am Eingang dieser Kennlinie liegt die Summe aus Trägersignal und Quellensignal an: $$ x(t) = z(t) + q(t) = A_{\rm T} \cdot \cos(\omega_{\rm T} t)+ q(t),\hspace{0.2cm} A_{\rm T} = 4\,{\rm V}\hspace{0.05cm}.$$ Über das Quellensignal $q(t)$ ist bekannt, dass es Spektralanteile zwischen $\text{1 kHz}$ und $\text{9kHz}$ (einschließlich dieser Grenzen) beinhaltet. Ab der Teilaufgabe e) soll folgendes Quellensignal vorausgesetzt werden: $$q(t) = A_{\rm 1} \cdot \cos(\omega_{\rm 1} t)+A_{\rm 9} \cdot \cos(\omega_{\rm 9} t) \hspace{0.05cm}.$$ Die Kreisfrequenzen seien $ω_1 = 2 π · 1 kHz$ und $ω_9 = 2 π · 9 kHz$. Die dazugehörigen Amplituden sind wie folgt gegeben: $A_1 = 1 V$ und $A_9 = 2 V$.

In den Fragen zu dieser Aufgabe werden folgende Abkürzungen verwendet: $$ y(t) = y_1(t) + y_2(t)+y_3(t),$$ $$y_1(t) = c_1 \cdot (z(t) + q(t)),$$ $$ y_2(t) = c_2 \cdot (z(t) + q(t))^2,$$ $$y_3(t) = c_3 \cdot (z(t) + q(t))^3 \hspace{0.05cm}.$$ Die Sendesignale $s(t)$ bzw. $s_1(t)$, $s_2(t)$ und $s_3(t)$ ergeben sich daraus jeweils durch eine Bandbegrenzung auf den Bereich von $\text{90 kHz}$ bis $\text{110 kHz}$.

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.1 Gegeben sind folgende trigonometrischen Umformungen: $$ \cos^2(\alpha) = {1}/{2} \cdot \left[ 1 + \cos(2\alpha)\right] \hspace{0.05cm},$$ $$\cos^3(\alpha) = {1}/{4} \cdot \left[ 3 \cdot \cos(\alpha) + \cos(3\alpha)\right] \hspace{0.05cm}.$$

Fragebogen

1

Wie sollte die Trägerfrequenz sinnvollerweise gewählt werden?

$f_T$ = $\text{kHz}$

2

Welche Signalanteile beinhaltet s1(t)?

	$c_1 \cdot z(t)$
	$c_1 \cdot q(t)$

3

Welche Signalanteile beinhaltet $s_2(t)$?

	$c_2 · z^2(t)$.
	$c_2 · q^2(t)$.
	$2c_2 · z(t) · q(t)$.

4

Welche Signalanteile beinhaltet $s_3(t)$ zumindest teilweise?

	$c_3 · z^3(t)$.
	$3 · c_3 · z^2(t) · q(t)$.
	$3 · c_3 · z(t) · q^2(t)$.
	$c_3 · q^3(t)$.

5

Berechnen Sie $s(t)$, wenn $c_3 = 0$ gilt und sich das Quellensignal $q(t)$ aus zwei Cosinusschwingungen zusammensetzt. Wie groß ist der Modulationsgrad?

$m$ =

6

Berechnen Sie nun das Sendesignal $s(t)$ unter der Voraussetzung $c_3 = 0.01/V^{2}$. Welche der nachfolgenden Aussagen treffen zu?

	Durch $c_3 ≠ 0$ wird die Spektrallinie bei $f_T$ verändert.
	Durch $c_3 ≠ 0$ entstehen lineare, kompensierbare Verzerrungen.
	Durch $c_3 ≠ 0$ entstehen nichtlineare, irreversible Verzerrungen.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.