Aufgaben:Exercise 2.3Z: DSB-AM due to Nonlinearity

• Return to book

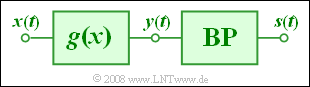
In dieser Aufgabe betrachten wir die Realisierung einer Zweiseitenband–Amplitudenmodulation mittels der nichtlinearen Kennlinie $$y = g(x) = c_1 \cdot x + c_2 \cdot x^2+ c_3 \cdot x^3\hspace{0.05cm}$$ $$ \Rightarrow c_1 = 2,\hspace{0.2cm}c_2 = 0.25/{\rm V},\hspace{0.2cm}c_3 = 0 \hspace{0.1cm}{\rm bzw.}\hspace{0.1cm}c_3 = 0.01/{\rm V^2}\hspace{0.05cm}.$$ Am Eingang dieser Kennlinie liegt die Summe aus Trägersignal und Quellensignal an: $$ x(t) = z(t) + q(t) = A_{\rm T} \cdot \cos(\omega_{\rm T} t)+ q(t),\hspace{0.2cm} A_{\rm T} = 4\,{\rm V}\hspace{0.05cm}.$$ Über das Quellensignal $q(t)$ ist bekannt, dass es Spektralanteile zwischen $\text{1 kHz}$ und $\text{9kHz}$ (einschließlich dieser Grenzen) beinhaltet. Ab der Teilaufgabe e) soll folgendes Quellensignal vorausgesetzt werden: $$q(t) = A_{\rm 1} \cdot \cos(\omega_{\rm 1} t)+A_{\rm 9} \cdot \cos(\omega_{\rm 9} t) \hspace{0.05cm}.$$ Die Kreisfrequenzen seien $ω_1 = 2 π · 1 kHz$ und $ω_9 = 2 π · 9 kHz$. Die dazugehörigen Amplituden sind wie folgt gegeben: $A_1 = 1 V$ und $A_9 = 2 V$.

In den Fragen zu dieser Aufgabe werden folgende Abkürzungen verwendet: $$ y(t) = y_1(t) + y_2(t)+y_3(t),$$ $$y_1(t) = c_1 \cdot (z(t) + q(t)),$$ $$ y_2(t) = c_2 \cdot (z(t) + q(t))^2,$$ $$y_3(t) = c_3 \cdot (z(t) + q(t))^3 \hspace{0.05cm}.$$ Die Sendesignale $s(t)$ bzw. $s_1(t)$, $s_2(t)$ und $s_3(t)$ ergeben sich daraus jeweils durch eine Bandbegrenzung auf den Bereich von $\text{90 kHz}$ bis $\text{110 kHz}$.

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.1 Gegeben sind folgende trigonometrischen Umformungen: $$ \cos^2(\alpha) = {1}/{2} \cdot \left[ 1 + \cos(2\alpha)\right] \hspace{0.05cm},$$ $$\cos^3(\alpha) = {1}/{4} \cdot \left[ 3 \cdot \cos(\alpha) + \cos(3\alpha)\right] \hspace{0.05cm}.$$

Fragebogen

1

Wie sollte die Trägerfrequenz sinnvollerweise gewählt werden?

$f_T$ = $\text{kHz}$

2

Welche Signalanteile beinhaltet s1(t)?

	$c_1 \cdot z(t)$
	$c_1 \cdot q(t)$

3

Welche Signalanteile beinhaltet $s_2(t)$?

	$c_2 · z^2(t)$.
	$c_2 · q^2(t)$.
	$2c_2 · z(t) · q(t)$.

4

Welche Signalanteile beinhaltet $s_3(t)$ zumindest teilweise?

	$c_3 · z^3(t)$.
	$3 · c_3 · z^2(t) · q(t)$.
	$3 · c_3 · z(t) · q^2(t)$.
	$c_3 · q^3(t)$.

5

Berechnen Sie $s(t)$, wenn $c_3 = 0$ gilt und sich das Quellensignal $q(t)$ aus zwei Cosinusschwingungen zusammensetzt. Wie groß ist der Modulationsgrad?

$m$ =

6

Berechnen Sie nun das Sendesignal $s(t)$ unter der Voraussetzung $c_3 = 0.01/V^{2}$. Welche der nachfolgenden Aussagen treffen zu?

	Durch $c_3 ≠ 0$ wird die Spektrallinie bei $f_T$ verändert.
	Durch $c_3 ≠ 0$ entstehen lineare, kompensierbare Verzerrungen.
	Durch $c_3 ≠ 0$ entstehen nichtlineare, irreversible Verzerrungen.

Musterlösung

Solution

1. Die Trägerfrequenz ist sinnvollerweise gleich der Mittenfrequenz des Bandpasses: $f_T = 100 kHz$. Eine „ZSB–AM” ergibt sich ebenfalls, wenn $f_T$ um nicht mehr als $±1 kHz$ davon abweicht.

2. $s_1(t)$ beinhaltet nur den Träger $z(t)$. Das Quellensignal $q(t)$ wird durch den Bandpass entfernt.

3. Der quadratische Term $z^2(t)$ besteht aus einem Gleichanteil (bei f = 0) sowie einem Anteil bei $2f_T$. Auch alle Spektralanteile von $q^2(t)$ liegen außerhalb des Bandpasses. Richtig ist somit die letzte Antwort.

4. Der Term $cos^3(ω_Tt)$ hat seinen größten Signalanteil bei $f = f_T$. Der dritte Lösungsvorschlag liegt zwischen $100 kHz ± 18 kHz$. Teile davon – nämlich die Frequenzanteile zwischen $90 kHz$ und $110 kHz$ – werden durch den Bandpass nicht entfernt und sind somit auch in $s(t)$ enthalten. Richtig sind somit die Lösungsvorschläge 1 und 3.

5.Das Sendesignal besteht aus insgesamt fünf Frequenzen: $$s(t) = c_1 \cdot A_{\rm T} \cdot \cos(\omega_{\rm T} t)+$$ $$ + c_2 \cdot A_{\rm T} \cdot A_{\rm 1} \cdot \cos((\omega_{\rm T} \pm \omega_{\rm 1})t) + c_2 \cdot A_{\rm T} \cdot A_{\rm 2} \cdot \cos((\omega_{\rm T} \pm \omega_{\rm 2})t) \hspace{0.05cm}.$$ Beachten Sie hierbei, dass der zweite und dritte Term jeweils zwei Signalfrequenzen (99 und 101 kHz bzw. 91 und 109 kHz) beinhaltet. Mit $A_T = 4 V,$ $A_1 = 1 V$, $A_9 = 2 V$, $c_1 = 1$ und $c_2 = 1/A_T = 0.25/V$ gilt auch: $$s(t) = 4\,{\rm V} \cdot \cos(\omega_{\rm T} t) + 1\,{\rm V} \cdot \cos((\omega_{\rm T} \pm \omega_{\rm 1})t) + 2\,{\rm V}\cdot \cos((\omega_{\rm T} \pm \omega_{\rm 2})t) \hspace{0.05cm}.$$ Daran erkennt man, dass der Modulationsgrad $m = (A_1 + A_2)/A_T = 0.75$ ist.

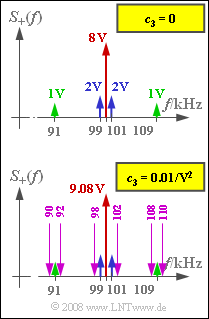
6.Die Grafik zeigt oben das Spektrum $S_+(f)$ – also nur positive Frequenzen – mit $c_3 = 0$. Mit $c_3 ≠ 0$ fallen folgende zusätzliche Spektralanteile an: $$c_3 \cdot z^3(t)= \frac{c_3 \cdot A_{\rm T}^3}{4} \cdot \left[ 3 \cdot \cos(\omega_{\rm T} t) + \cos(3\omega_{\rm T} t)\right] \hspace{0.05cm}.$$ Dabei fällt der erste Anteil in den Durchlassbereich des Bandpasses. Das Diracgewicht bei $f_T = 100 kHz$ wird dadurch von ursprünglich 8 V auf 8 V + 0.75 · 0.01/V2 · 43 V3 = 8.48 V erhöht.

Weiterhin liefert der dritte Spektralanteil von Teilaufgabe d) einen unerwünschten Beitrag zu $S_+(f)$. Dabei gilt: $$q^2(t) = \left[A_{\rm 1} \cdot \cos(\omega_{\rm 1} t)+A_{\rm 9} \cdot \cos(\omega_{\rm 9} t)\right]^2 =$$ $$= A_{\rm 1}^2 \cdot \cos^2(\omega_{\rm 1} t)+ A_{\rm 9}^2 \cdot \cos^2(\omega_{\rm 9}t) +$$ $$ + 2 \cdot A_{\rm 1} \cdot A_{\rm 9} \cdot \cos(\omega_{\rm 1} t)\cdot \cos(\omega_{\rm 9} t)$$ $$ \Rightarrow \hspace{0.2cm} q^2(t) = \frac{A_{\rm 1}^2}{2} +\frac{A_{\rm 1}^2}{2} \cdot \cos(\omega_{\rm 2} t)+ \frac{A_{\rm 9}^2}{2} + \frac{A_{\rm 9}^2}{2} \cdot \cos(\omega_{\rm 18} t) +$$ $$ + A_{\rm 1} \cdot A_{\rm 9} \cdot \cos(\omega_{\rm 8} t)+ A_{\rm 1} \cdot A_{\rm 9} \cdot \cos(\omega_{\rm 10} t)$$ Nach der Multiplikation mit $z(t)$ fallen alle diese Beiträge bis auf den vierten in den Bereich von 90 kHz bis 110 kHz. Das Gewicht bei fT wird um $3 · c_3 · A_T · 0.5 (A_1^2 + A_g^2) = 0.6 V$ weiter erhöht und ist somit 9.08 V. Weitere Anteile ergeben sich bei:

• 98 kHz und 102 kHz mit den Gewichten $c_3 · A_T/2 · A_1^2/2 = 0.03 V$,
• 92 kHz und 108 kHz mit den Gewichten $3c_3 · A_T/2 · A_1 · A_9 = 0.12 V$,
• 90 kHz und 110 kHz mit den Gewichten $3c_3 · A_T/2 · A_1 · A_9 = 0.12 V$.

Die untere Grafik zeigt das Spektrum $S_+(f)$ unter Berücksichtigung der kubischen Anteile. Man erkennt, dass neue Frequenzen entstanden sind, was auf nichtlineare Verzerrungen hindeutet. Richtig sind somit die Lösungsvorschläge 1 und 3.