Aufgaben:Exercise 2.5Z: Linear Distortions with DSB-AM

• Return to book

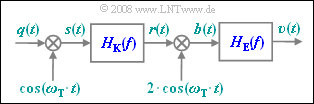
Auch in dieser Zusatzaufgabe wird wie in A2.5 die Kombination ZSB–AM/Synchrondemodulator bei Berücksichtigung eines linear verzerrenden Kanals untersucht.

Das Quellensignal $q(t)$ sei ein Cosinussignal mit Amplitude $A_N$ und Frequenz $f_N$, so dass das Spektrum des modulierten Signals wie folgt lautet: $$S(f)= \frac{A_{\rm N}}{4} \cdot \left[\delta(f + f_{\rm O}) + \delta(f + f_{\rm U}) + \delta(f - f_{\rm U}) + \delta(f - f_{\rm O}) \right]\hspace{0.05cm}.$$ Die Abkürzungen stehen für $f_O = f_T + f_N$ (oberes Seitenband) und $f_U = f_T – f_N$ (unteres Seitenband). Der Kanalfrequenzgang ist nur für diese beiden Frequenzen gegeben und lautet: $$ H_{\rm K}(f_{\rm O}) = R_{\rm O} + {\rm j} \cdot I_{\rm O},\hspace{0.2cm}H_{\rm K}(f_{\rm U}) = R_{\rm U} + {\rm j} \cdot I_{\rm U} \hspace{0.05cm}.$$ Für negative Frequenzen gilt stets $H_K(– f) = H_K*(f)$.

Verwenden Sie bei numerischen Berechnungen folgende Zahlenwerte: $$A_{\rm N} = 2\,{\rm V}, \hspace{0.15cm}f_{\rm N} = 3\,{\rm kHz}, \hspace{0.15cm}f_{\rm T} = 30\,{\rm kHz} \hspace{0.05cm},$$ $$R_{\rm U} = 0.8, \hspace{0.15cm}I_{\rm U} = -0.2, \hspace{0.15cm}R_{\rm O} = 0.4, \hspace{0.15cm}I_{\rm O} = -0.2 \hspace{0.05cm}.$$ In der Teilaufgabe c) soll die Lösung über den resultierenden Frequenzgang von Modulator, Kanal und Demodulator erfolgen: $$H_{\rm MKD}(f) = {1}/{2} \cdot \left[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\right]\hspace{0.05cm}.$$ Abschließend wird in der Teilaufgabe d) der folgende Kanalfrequenzgang betrachtet (die Darstellung gilt nur für positive Frequenzen): $$ H_{\rm K}(f) = \frac{1}{1 + 3{\rm j} \cdot ({f}/{f_{\rm T}} - 1)}\hspace{0.05cm}.$$ Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.2.

Fragebogen

1

{Berechnen und skizzieren Sie das Spektrum $R(f)$ am Kanalausgang ($R_U = 0.8$, $I_U = –0.2$, $R_O = 0.4$, $I_O = –0.2$). Wie lautet die Spektrallinie bei $–f_O$?

$Re[R(– f_O)]$ = $\text{V}$

$Im[R(– f_O)]$ = $\text{V}$

2

Wie lautet das Sinkensignal $υ(t)$? Berücksichtigen Sie bei der Berechnung auch den Tiefpass des Synchrondemodulators. Wie groß ist der Signalwert bei t = 0?

$ υ(t = 0)$ = $\text{V}$

3

Berechnen Sie nun das Sinkensignal $υ(t)$ über den resultierenden Frequenzgang $H_{MKD}(f)$ und bewerten Sie den Rechengang.

	Die Berechnung gemäß Teilaufgabe b) führt schneller zum Erfolg.
	Die Berechnung gemäß Teilaufgabe c) führt schneller zum Erfolg.

4

Berechnen Sie $υ(t)$ für den Kanalfrequenzgang $H_K(f) = (1 + 3j · (f/f_T–1))^{–1}$. Wie groß ist der Signalwert bei t = 0?

$v(t=0)$ = $\text{V}$

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.