Aufgaben:Exercise 2.10: SSB-AM with Channel Distortions

• Return to book

Wir betrachten die Übertragung des Quellensignals $$q(t) = 2\,{\rm V} \cdot \cos(2 \pi f_2 t) + 2\,{\rm V} \cdot \cos(2 \pi f_4 t)$$ über einen Gauß–Bandpasskanal mit der Mittenfrequenz $f_M = 48 kHz$. Diese unterscheidet sich von der bei der Modulation verwendeten Trägerfrequenz $f_T = 50 kHz$. Die Frequenzen $f_2$ und $f_4$ stehen als Abkürzungen für 2 kHz bzw. 4 kHz.

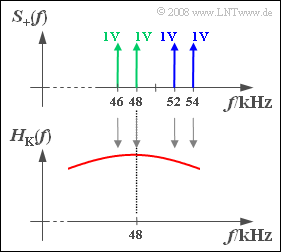
Untersucht werden sollen folgende Modulationsverfahren mit dem jeweiligen Spektrum $S_+(f)$ – des analytischen Signals – entsprechend der oberen Grafik:

• ZSB–AM (alle vier Spektrallinien bei 46 kHz, 48 kHz, 52 kHz und 54 kHz),
• OSB–AM (blaue Spektrallinien bei 52 kHz und 54 kHz),
• USB–AM (grüne Spektrallinien bei 46 kHz und 48 kHz).

Verwendet wird jeweils ein Synchrondemodulator, der zunächst das empfängerseitige Trägersignal $$ z_{\rm E} (t) = \left\{ \begin{array}{c} 2 \cdot z(t) \\ 4 \cdot z(t) \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm ZSB} \hspace{0.05cm}, \\ {\rm OSB, USB} \hspace{0.05cm} \\ \end{array}$$ multiplikativ zusetzt und anschließend die Anteile um die doppelte Trägerfrequenz vollständig unterdrückt. Bei idealem Kanal $H_K(f) = 1$ würde somit in allen Fällen $υ(t) = q(t)$ gelten.

Der hier betrachtete Gaußkanal ist durch folgende Stützwerte gegeben: $$ H_{\rm K}(f = 46\,{\rm kHz}) = 0.968,\hspace{0.3cm}H_{\rm K}(f = 48\,{\rm kHz}) = 1.000,$$ $$ H_{\rm K}(f = 52\,{\rm kHz}) = 0.882,\hspace{0.3cm}H_{\rm K}(f = 54\,{\rm kHz}) = 0.754\hspace{0.05cm}.$$ Schreiben Sie das Sinkensignal jeweils in der Form $$v(t) = A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2)) + A_4 \cdot \cos(2 \pi f_4 \cdot (t - \tau_4))\hspace{0.05cm}.$$ Alle Berechnungen sind sowohl für eine perfekte Phasensynchronisation ($Δϕ_T = 0$) als auch für einen Phasenversatz von $Δϕ_T = 30°$ durchzuführen. Dieser liegt zum Beispiel dann vor, wenn das sendeseitige Trägersignal cosinusförmig verläuft und für das empfangsseitige Trägersignal gilt: $$ z_{\rm E} (t) = A_{\rm E} \cdot \cos(\omega_{\rm T} \cdot t - 30^\circ) . $$ Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.2 und Kapitel 2.4.

Fragebogen

1

Berechnen Sie die Amplituden bei ZSB–AM und perfekter Synchronisation.

$ZSB, Δϕ_T = 0: A_2$ = $V$

$ZSB, Δϕ_T = 0: A_4$ = $V$

2

Wie lauten die Größen A2 und τ2 bei ZSB–AM und $Δϕ_T = 30°$ Phasenversatz?

$ZSB, Δϕ_T = 30°: A_2$ = $V$

$ZSB, Δϕ_T = 30°: τ_2$ = $μs$

3

Berechnen Sie die Amplituden $A_2$ und $A_4$ bei OSB–AM und $Δϕ_T = 0$.

$OSB, Δϕ_T = 0: A_2$ = $V$

$OSB, Δϕ_T = 0: A_4$ = $V$

4

Geben Sie die Signalsamplituden für USB–AM und $Δϕ_T = 0$ an.

$USB, Δϕ_T = 0: A_2$ = $V$

$USB, Δϕ_T = 0: A_4$ = $V$

5

Wie lauten dagegen die Signalparameter bei USB–AM und ΔϕT = 30°?

$USB, Δϕ_T = 30°: A_2$ = $V$

$USB, Δϕ_T = 30°: τ_2$ = $μs$

$USB, Δϕ_T = 30°: A_4$ = $V$

$USB, Δϕ_T = 30°: τ_4$ = $μs$

6

Welche dieser Aussagen sind nach Ihren Ergebnissen zutreffend? Hierbei sollen unter „Kanalverzerrungen” stets Dämpfungsverzerrungen verstanden werden.

	Kanalverzerrung führt bei ZSB-AM zu Dämpfungsverzerrungen.
	Kanalverzerrung führt bei ESB–AM zu Phasenverzerrungen.
	Ein Phasenversatz führt bei ZSB–AM zu Dämpfungsverzerrungen.
	Ein Phasenversatz führt bei ESB–AM zu Phasenverzerrungen.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.