Aufgaben:Exercise 2.13: Quadrature Amplitude Modulation

• Return to book

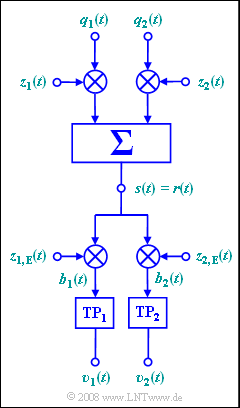
Die durch die Grafik erklärte Quadratur–Amplitudenmodulation erlaubt unter gewissen Randbedingungen, die in dieser Aufgabe angegeben werden sollen, die gleichzeitige Übertragung von zwei Quellensignalen $q_1(t)$ und $q_2(t)$ über den gleichen Kanal. In dieser Aufgabe gelte mit $A_1 = A_2 = 2 V$: $$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$ $$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$ Die vier in der Grafik eingezeichneten Trägersignale lauten mit $ω_T = 2π · 25 kHz$: $$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$ $$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$ $$ z_{1,{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$ $$ z_{2,{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$ Die beiden Tiefpässe mit den Eingangssignalen $b_1(t)$ und $b_2(t)$ entfernen jeweils alle Frequenzanteile $|f| > f_T$.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 2.5 dieses Buches. Anzumerken ist, dass hier die Trägersignale $z_2(t)$ und $z_{2,E}(t)$ mit positivem Vorzeichen angesetzt wurden. Oft – so auch im Theorieteil – werden diese Trägersignale als „Minus–Sinus” angegeben.

Gegeben sind folgende trigonometrischen Umformungen: $$\cos(\alpha) \cdot \cos(\beta) = \frac{1}{2} \cdot \left[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \right],$$ $$ \sin(\alpha) \cdot \sin(\beta) = \frac{1}{2} \cdot \left[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \right],$$ $$\sin(\alpha) \cdot \cos(\beta) = \frac{1}{2} \cdot \left[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \right] \hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie das Sendesignal $s(t)$ für den Fall $f1 ≠ f2$. Welche der folgenden Aussagen treffen zu?

	$s(t)$ besteht aus zwei Cosinus– und zwei Sinusschwingungen.
	$s(t)$ setzt sich aus vier Cosinusschwingungen zusammen.
	$s(t)$ setzt sich aus vier Sinusschwingungen zusammen.

2

Wie lautet $s(t)$ für $f1 = f2 = 5 kHz$. Welcher Signalwert tritt bei $t = 50 μs$ auf?

$s(t = 50 μs)$ = $V$

3

Berechnen Sie für $f1 = f2$ und $Δϕ_T = 0$ die Sinkensignale $υ1(t)$ und $υ2(t)$. Welche der folgenden Aussagen treffen zu?

	Es gilt $υ_1(t) = q_1(t)$ und $υ_2(t) = q_2(t)$.
	Es ergeben sich lineare Verzerrungen.
	Es ergeben sich nichtlineare Verzerrungen.

4

Berechnen Sie für $f1 = f2$ und $Δϕ_T = 30°$ die Sinkensignale $υ1(t)$ und $υ2(t)$. Welche der folgenden Aussagen treffen zu?

	Es gilt $υ_1(t) = q_1(t)$ und $υ_2(t) = q_2(t)$.
	Es ergeben sich lineare Verzerrungen.
	Es ergeben sich nichtlineare Verzerrungen.

5

Welche der folgenden Aussagen treffen für $f1 ≠ f2$ und $Δϕ_T ≠ 0$ zu?

	Es gilt $υ_1(t) = q_1(t)$ und $υ_2(t) = q_2(t)$.
	Es ergeben sich lineare Verzerrungen.
	Es ergeben sich nichtlineare Verzerrungen.

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.