Difference between revisions of "Aufgaben:Exercise 3.1: Phase Modulation Locus Curve"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Phasenmodulation (PM) }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |typ…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID1079__Mod_A_3_1.png|right|]] |
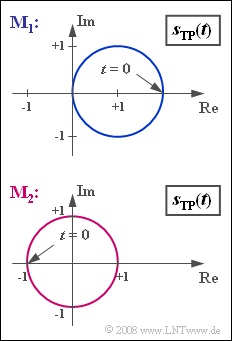
| + | Die Grafik zeigt Ortskurven am Ausgang zweier Modulatoren $M_1$ und $M_2$. Real- und Imaginärteil sind in dieser Grafik jeweils auf 1 V normiert. | ||
| + | Unter der Ortskurve versteht man allgemein die Darstellung des äquivalenten Tiefpass–Signals $s_{TP}(t)$ in der komplexen Ebene. | ||
| + | |||
| + | Das Quellensignal sei bei beiden Modulatoren gleich: | ||
| + | $$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm}\\{\rm mit}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| + | Einer der beiden Modulatoren realisiert eine Phasenmodulation, die durch folgende Gleichungen gekennzeichnet ist: | ||
| + | $$ s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \phi(t) \right)\hspace{0.05cm},$$ | ||
| + | $$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$ | ||
| + | $$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$ | ||
| + | Den Maximalwert von $ϕ(t)$ nennt man Modulationsindex $η$ – teilweise wird diese Größe in der Literatur auch als Phasenhub bezeichnet. | ||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [http://en.lntwww.de/Modulationsverfahren/Phasenmodulation_(PM) Kapitel 3.1]. | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Welches Modulationsverfahren verwendet der Modulator $M_1$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Zweiseitenband–Amplitudenmodulation. |
| − | + | + | + Einseitenband–Amplitudenmodulation. |
| + | - Phasenmodulation. | ||
| + | {Welches Modulationsverfahren verwendet der Modulator $M_2$? | ||
| + | |type="[]"} | ||
| + | - Zweiseitenband–Amplitudenmodulation. | ||
| + | - Einseitenband–Amplitudenmodulation. | ||
| + | + Phasenmodulation. | ||
| − | { | + | {Wie groß ist die Trägeramplitude $A_T$ beim Phasenmodulator? Beachten Sie die Normierung auf 1 V. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $A_T$ = { 1 3% } $V$ |
| + | {Welche Werte besitzen der Modulationsindex und die Modulatorkonstante? | ||
| + | |type="{}"} | ||
| + | $η$ = { 3.1415 3% } | ||
| + | $K_{PM}$ = { 1.571 3% } $1/V$ | ||
| + | |||
| + | {Beschreiben Sie die Bewegung auf der Ortskurve. Zu welcher Zeit $t_1$ wird zum ersten Mal wieder der Ausgangspunkt $s_{TP}(t = 0) = –1V$ erreicht? | ||
| + | |type="{}"} | ||
| + | $t_1$ = { 100 3% } $μs$ | ||
| Line 25: | Line 50: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Es handelt sich um eine ESB–AM mit dem Seitenband–zu–Träger–Verhältnis $μ = 1$ ⇒ Antwort 2. Bewegt man sich auf dem Kreis in mathematisch positive Richtung, so liegt speziell eine OSB–AM vor, andernfalls eine USB–AM. |
| − | '''2.''' | + | |
| − | '''3.''' | + | Die Phasenfunktion $ϕ(t)$ als der Winkel eines Punktes $s_{TP}(t)$ auf dem Kreis(bogen) bezogen auf den Koordinatenursprung kann Werte zwischen $±π/2$ annehmen und zeigt keinen Cosinusverlauf. Aber auch die Hüllkurve $a(t) = |s_{TP}(t)|$ ist nicht cosinusförmig. Würde man beim Empfänger für M1 einen Hüllkurvendemodulator einsetzen, so käme es zu nichtlinearen Verzerrungen im Gegensatz zur ZSB–AM, deren Ortskurve eine horizontale Gerade ist. |
| − | '''4.''' | + | |
| − | + | ||
| − | + | '''2.'''Hier handelt es sich um die Phasenmodulation ⇒ Antwort 3. Die Einhüllende $a(t) = A_T$ ist konstant, während die Phase $ϕ(t)$ entsprechend dem Quellensignal cosinusförmig verläuft. | |
| − | ''' | + | |
| + | '''3.''' Bei der Phasenmodulation gilt | ||
| + | $$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$ | ||
| + | Aus der Grafik kann man die Trägeramplitude $A_T = 1 V$ als den Kreisradius ablesen. | ||
| + | |||
| + | |||
| + | '''4.'''Das Quellensignal $q(t)$ ist zum Zeitpunkt $t = 0$ maximal und damit auch die Phasenfunktion: | ||
| + | $$ \eta = \phi_{\rm max} = \phi( t =0)\hspace{0.15cm}\underline { = \pi} \hspace{0.05cm}.$$ | ||
| + | Daraus erhält man für die Modulatorkonstante: | ||
| + | $$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$ | ||
| + | |||
| + | '''5.'''Man bewegt sich auf dem Kreis(bogen) im Uhrzeigersinn. Nach einem Viertel der Periodendauer $T_N = 1/f_N = 200 μs$ ist $ϕ(t) = 0$ und $s_{TP}(t) = 1 V$. Zur Zeit $t_1 = T_N/2 = 100 μs$ gilt $ϕ(t_1) = –π$ und $s_{TP}(t_1) = –1 V$. Danach bewegt man sich auf dem Kreisbogen entgegen dem Uhrzeigersinn. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 14:23, 2 January 2017
Die Grafik zeigt Ortskurven am Ausgang zweier Modulatoren $M_1$ und $M_2$. Real- und Imaginärteil sind in dieser Grafik jeweils auf 1 V normiert. Unter der Ortskurve versteht man allgemein die Darstellung des äquivalenten Tiefpass–Signals $s_{TP}(t)$ in der komplexen Ebene.
Das Quellensignal sei bei beiden Modulatoren gleich:
$$ q(t) = A_{\rm N} \cdot \cos(2 \pi f_{\rm N} \cdot t),\hspace{1cm}\\{\rm mit}\hspace{0.2cm} A_{\rm N} = 2\,{\rm V},\hspace{0.2cm}f_{\rm N} = 5\,{\rm kHz}\hspace{0.05cm}.$$
Einer der beiden Modulatoren realisiert eine Phasenmodulation, die durch folgende Gleichungen gekennzeichnet ist:
$$ s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \phi(t) \right)\hspace{0.05cm},$$
$$ s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm},$$
$$ \phi(t) = K_{\rm PM} \cdot q(t)\hspace{0.05cm}.$$
Den Maximalwert von $ϕ(t)$ nennt man Modulationsindex $η$ – teilweise wird diese Größe in der Literatur auch als Phasenhub bezeichnet.
Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.1.
Fragebogen
Musterlösung
Die Phasenfunktion $ϕ(t)$ als der Winkel eines Punktes $s_{TP}(t)$ auf dem Kreis(bogen) bezogen auf den Koordinatenursprung kann Werte zwischen $±π/2$ annehmen und zeigt keinen Cosinusverlauf. Aber auch die Hüllkurve $a(t) = |s_{TP}(t)|$ ist nicht cosinusförmig. Würde man beim Empfänger für M1 einen Hüllkurvendemodulator einsetzen, so käme es zu nichtlinearen Verzerrungen im Gegensatz zur ZSB–AM, deren Ortskurve eine horizontale Gerade ist.
2.Hier handelt es sich um die Phasenmodulation ⇒ Antwort 3. Die Einhüllende $a(t) = A_T$ ist konstant, während die Phase $ϕ(t)$ entsprechend dem Quellensignal cosinusförmig verläuft.
3. Bei der Phasenmodulation gilt $$s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t) }\hspace{0.05cm}.$$ Aus der Grafik kann man die Trägeramplitude $A_T = 1 V$ als den Kreisradius ablesen.
4.Das Quellensignal $q(t)$ ist zum Zeitpunkt $t = 0$ maximal und damit auch die Phasenfunktion:
$$ \eta = \phi_{\rm max} = \phi( t =0)\hspace{0.15cm}\underline { = \pi} \hspace{0.05cm}.$$
Daraus erhält man für die Modulatorkonstante:
$$K_{\rm PM} = \frac{\eta}{A_{\rm N}} = \frac{\pi}{2\,{\rm V}}\hspace{0.15cm}\underline {= 1.571\,{\rm V}^{-1}}\hspace{0.05cm}.$$
5.Man bewegt sich auf dem Kreis(bogen) im Uhrzeigersinn. Nach einem Viertel der Periodendauer $T_N = 1/f_N = 200 μs$ ist $ϕ(t) = 0$ und $s_{TP}(t) = 1 V$. Zur Zeit $t_1 = T_N/2 = 100 μs$ gilt $ϕ(t_1) = –π$ und $s_{TP}(t_1) = –1 V$. Danach bewegt man sich auf dem Kreisbogen entgegen dem Uhrzeigersinn.