Difference between revisions of "Aufgaben:Exercise 4.2Z: About the Sampling Theorem"
| Line 73: | Line 73: | ||
'''3.''' Beim cosinusförmigen Signal ergibt sich entsprechend der nachfolgenden Grafik mit $f_A = 10 kHz$ das Spektrum $Q_A(f)$: Alle Spektrallinien sind reell. Die Periodifizierung von $Q(f)$ mit $f_A = 10 kHz$ führt zu einem Diracpuls mit Spektrallinien bei $±f_N$, $±f_N$ $± f_A$, $±f_N$ $± 2f_A$, usw.. Durch die Überlagerungen haben alle Diracfunktionen das Gewicht A, während die beiden Spektrallinien von $Q(f)$ nur jeweils mit $A/2$ gewichtet sind. Wegen $H(f = f_N) = H(f = f_G) = 0.5$ ist das Spektrum $V_1(f)$ nach dem Tiefpass identisch mit $Q_1(f)$ und dementsprechend gilt auch $υ-1(t) = q_1(t)$. | '''3.''' Beim cosinusförmigen Signal ergibt sich entsprechend der nachfolgenden Grafik mit $f_A = 10 kHz$ das Spektrum $Q_A(f)$: Alle Spektrallinien sind reell. Die Periodifizierung von $Q(f)$ mit $f_A = 10 kHz$ führt zu einem Diracpuls mit Spektrallinien bei $±f_N$, $±f_N$ $± f_A$, $±f_N$ $± 2f_A$, usw.. Durch die Überlagerungen haben alle Diracfunktionen das Gewicht A, während die beiden Spektrallinien von $Q(f)$ nur jeweils mit $A/2$ gewichtet sind. Wegen $H(f = f_N) = H(f = f_G) = 0.5$ ist das Spektrum $V_1(f)$ nach dem Tiefpass identisch mit $Q_1(f)$ und dementsprechend gilt auch $υ-1(t) = q_1(t)$. | ||
| + | |||
| + | |||
[[File:P_ID1612__Mod_Z_4_2c.png|P_ID1612__Mod_Z_4_2c.png]] | [[File:P_ID1612__Mod_Z_4_2c.png|P_ID1612__Mod_Z_4_2c.png]] | ||
Revision as of 15:23, 4 January 2017
Das Abtasttheorem besagt, dass die Abtastfrequenz $f_A = 1/T_A$ mindestens doppelt so groß sein muss wie die größte im Quellensignal $q(t)$ enthaltene Frequenz $f_{N,max}$: $$f_{\rm A} \ge 2 \cdot f_{\rm N,\hspace{0.05cm}max}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm A} \le \frac{1}{2 \cdot f_{\rm N, \hspace{0.05cm}max}}\hspace{0.05cm}.$$ Wird diese Bedingung erfüllt, so kann beim Empfänger das Nachrichtensignal durch einen rechteckförmigen (idealen) Tiefpass mit dem Frequenzgang $$H(f) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm G},} \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| = f_{\rm G},} \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm G}} \\ \end{array}$$ vollständig rekonstruiert werden, das heißt, es gilt dann $υ(t) = q(t)$. Die Grenzfrequenz $f_G$ ist dabei gleich der halben Abtastfrequenz zu wählen. Das Gleichheitszeichen gilt allgemein nur dann, wenn das Spektrum $Q(f)$ keine diskrete Spektrallinie bei der Frequenz $f_{N, max}$ beinhaltet.
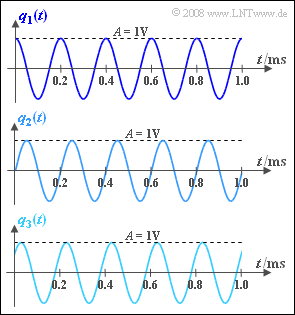
In dieser Aufgabe werden drei verschiedene Quellensignale betrachtet, die sich jeweils als harmonische Schwingung $$q(t) = A \cdot \cos (2 \pi \cdot f_{\rm N} \cdot t - \varphi)$$ mit der Amplitude $A = 1 V$ und der Frequenz $f_N = 5 kHz$ darstellen lassen. Für die Spektralfunktion $Q(f)$ aller dargestellten Zeitsignale gilt allgemein: $$Q(f) = \frac{A}{2} \cdot \delta (f- f_{\rm N}) \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm}\varphi}+ \frac{A}{2} \cdot \delta (f+ f_{\rm N}) \cdot {\rm e}^{+{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm}\varphi}\hspace{0.05cm}.$$ Die in der Grafik skizzierten Schwingungen unterscheiden sich allein durch die Phase $φ$:
- $φ_1 = 0$ ⇒ Cosinussignal $q_1(t)$,
- $φ_2 = π/2 (= 90°)$ ⇒ Sinussignal $q_2(t)$,
- $φ_3 = π/4 (= 45°)$ ⇒ Signal $q_3(t)$.
Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1 Das abgetastete Quellensignal wird mit $q_A(t)$ bezeichnet und dessen Spektralfunktion mit $Q_A(f)$. Die Abtastung erfolgt stets bei $ν · T_A$.
Fragebogen
Musterlösung
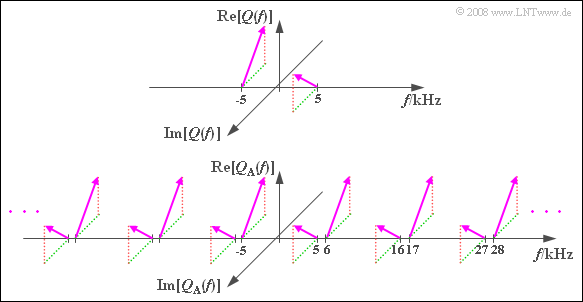
Die Verschiebung um
- $f_A = 11 kHz$ liefert Spektrallinien bei 6 kHz und 16 kHz,
- $–f_A = –11 kHz$ liefert Spektrallinien bei –6 kHz und –16 kHz,
- $2 · f_A = 22 kHz$ liefert Spektrallinien bei 17 kHz und 27 kHz,
- $–2 · f_A = –22 kHz$ liefert Spektrallinien bei –17 kHz und –27 kHz.
Durch einen rechteckförmigen Tiefpass mit der Grenzfrequenz $f_G = f_A/2 = 5.5 kHz$ erhält man wieder das ursprüngliche Spektrum $Q(f)$.
2. Der Abtastabstand ist gleich dem Kehrwert der Abtastfrequenz: $$ T_{\rm A} = \frac{1}{f_{\rm A} }\hspace{0.15cm}\underline { = 0.1\,{\rm ms}} \hspace{0.05cm}.$$
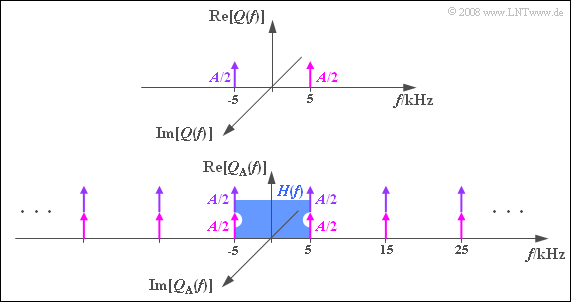
3. Beim cosinusförmigen Signal ergibt sich entsprechend der nachfolgenden Grafik mit $f_A = 10 kHz$ das Spektrum $Q_A(f)$: Alle Spektrallinien sind reell. Die Periodifizierung von $Q(f)$ mit $f_A = 10 kHz$ führt zu einem Diracpuls mit Spektrallinien bei $±f_N$, $±f_N$ $± f_A$, $±f_N$ $± 2f_A$, usw.. Durch die Überlagerungen haben alle Diracfunktionen das Gewicht A, während die beiden Spektrallinien von $Q(f)$ nur jeweils mit $A/2$ gewichtet sind. Wegen $H(f = f_N) = H(f = f_G) = 0.5$ ist das Spektrum $V_1(f)$ nach dem Tiefpass identisch mit $Q_1(f)$ und dementsprechend gilt auch $υ-1(t) = q_1(t)$.
Im Zeitbereich kann man sich die Signalrekonstruktion wie folgt vorstellen: Die Abtastwerte von $q_1(t)$ liegen genau bei den Signalmaxima und –minima. Der Tiefpass formt daraus das Cosinussignal mit richtiger Amplitude, Frequenz und Phase. Richtig ist demnach der Lösungsvorschlag 2.
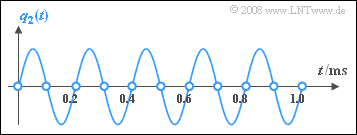
4. Alle Abtastwerte von $q_2(t)$ liegen nun genau bei den Nulldurchgängen des Sinussignals, das heißt, dass hier $q_A(t) = 0$ gilt. Damit ergibt sich aber natürlich auch $υ_2(t) = 0$. ⇒ Lösungsvorschlag 3 ist richtig.
Im Spektralbereich kann man das Ergebnis mit Hilfe der Grafik zur Teilaufgabe a) herleiten. $Q(f)$ ist rein imaginär und die Imaginärteile bei $±f_N$ haben unterschiedliche Vorzeichen. Somit heben sich bei der Periodifizierung jeweils ein positiver und ein negativer Anteil auf ⇒ $Q_A(f) = 0$ ⇒ $V_2(f) = 0$.
5. Von den vorgegebenen Lösungsvorschlägen ist keiner richtig. Ersetzt man in der Grafik zur Aufgabe a) die Abtastfrequenz $f_A = 11 kHz$ durch $f_A = 10 kHz$, so addieren sich zwar die Realteile, aber die Imaginärteile löschen sich aus. Das heißt, dass nun $Q_A(f)$ und $V_3(f)$ reelle Spektren sind. Das heißt weiter: Die Phaseninformation geht verloren (φ = 0) und das Ausgangssignal $υ_3(t)$ ist ein Cosinussignal. Die Signale $q_3(t)$ und $υ_3(t)$ unterscheiden sich somit sowohl in der Amplitude als auch in der Phase.
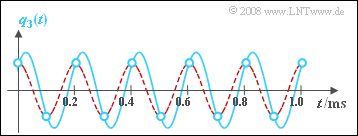
Die Grafik zeigt türkisfarben das Signal $q_3(t)$, dessen Abtastwerte (Kreise) sowie rot gestrichelt das Ausgangssignal $υ_3(t)$ des Tiefpasses. Man erkennt, dass der Tiefpass genau das Ergebnis liefert, für das wahrscheinlich auch Sie sich entscheiden würden, wenn Sie durch die Abtastwerte einen Kurvenzug einzeichnen sollten. Keines der vorgegebenen Lösungsvorschläge trifft zu.