Difference between revisions of "Mobile Communications/Non-Frequency-Selective Fading With Direct Component"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Zeitvariante Übertragungskanäle |Vorherige Seite=Statistische Bindungen innerhalb des Rayleigh–Prozesses |Nächste Seite=Allgemeine…“) |
|||
| Line 38: | Line 38: | ||
*Im Gegensatz zu <i>Rayleigh</i> (mit <i>z</i><sub>0</sub> = 0) ist die Phase bei <i>Rice–Fading</i> nicht gleichverteilt, sondern es gibt eine Vorzugsrichtung <i>ϕ</i><sub>0</sub> = arctan(<i>y</i><sub>0</sub>/<i>x</i><sub>0</sub>). Oft setzt man <nobr><i>y</i><sub>0</sub> = 0</nobr> ⇒ <i>ϕ</i><sub>0</sub> = 0.<br> | *Im Gegensatz zu <i>Rayleigh</i> (mit <i>z</i><sub>0</sub> = 0) ist die Phase bei <i>Rice–Fading</i> nicht gleichverteilt, sondern es gibt eine Vorzugsrichtung <i>ϕ</i><sub>0</sub> = arctan(<i>y</i><sub>0</sub>/<i>x</i><sub>0</sub>). Oft setzt man <nobr><i>y</i><sub>0</sub> = 0</nobr> ⇒ <i>ϕ</i><sub>0</sub> = 0.<br> | ||
| + | == Beispielhafte Signalverläufe bei Rice–Fading (1) == | ||
| + | <br> | ||
| + | Die Grafik zeigt Signalverläufe und Dichtefunktionen zweier Mobilfunkkanäle: | ||
| + | *Rayleigh–Fading mit E[|<i>z</i>(<i>t</i>)|<sup>2</sup>] = 2<i>σ</i><sup>2</sup> = 1 (blaue Kurven),<br> | ||
| + | *Rice–Fading mit gleichem <i>σ</i> sowie <i>x</i><sub>0</sub> = 0.707 und <i>y</i><sub>0</sub> = –0.707 (rote Kurven).<br><br> | ||
| + | Für die Erzeugung der Signalausschnitte mit dem auf der letzten Seite gezeigten Modell wurde in beiden Fällen die maximale Dopplerfrequenz <nobr><i>f</i><sub>D, max</sub> = 100 Hz</nobr> zugrundegelegt. AKF und LDS von Rayleigh– und Rice–Fading unterscheiden sich nur geringfügig. Es gilt: | ||
| + | :<math>\varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.1cm} = \hspace{-0.1cm} \varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} + |z_0|^2 \hspace{0.05cm},</math> | ||
| + | :<math> {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.1cm} = \hspace{-0.1cm} {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} + |z_0|^2 \cdot \delta (f_{\rm D}) \hspace{0.05cm}.</math> | ||
| + | Berücksichtigt ist, dass die Spektraldarstellung eines Gleichanteils zu einer Diracfunktion führt.<br> | ||
| + | |||
| + | [[File:P ID2129 Mob T 1 4 S2 v1.png|Vergleich von Rayleigh-Fading (blau) und Rice-Fading (rot)|class=fit]]<br> | ||
| + | |||
| + | Die Bildbeschreibung folgt auf der nächsten Seite.<br> | ||
{{Display}} | {{Display}} | ||
Revision as of 19:04, 5 January 2017
Kanalmodell und Rice–WDF
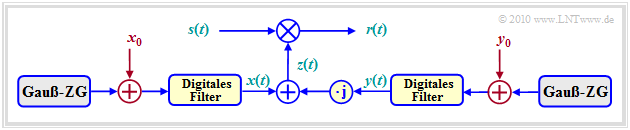
Die Rayleigh–Verteilung beschreibt den Mobilfunkkanal unter der Annahme, dass kein direkter Pfad vorhanden ist und sich somit der multiplikative Faktor z(t) allein aus diffus gestreuten Komponenten zusammensetzt. Bei Vorhandensein einer Direktkomponente (englisch: Line of Sight, LoS) muss man im Modell zu den mittelwertfreien Gaußprozessen x(t) und y(t) noch Gleichkomponenten hinzufügen:
\[x(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} x(t) +x_0 \hspace{0.05cm}, \hspace{0.2cm} y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} y(t) +y_0\hspace{0.05cm},\]
\[z(t) = x(t) + {\rm j} \cdot y(t) \hspace{0.1cm} \Rightarrow \hspace{0.1cm} z(t) +z_0 \hspace{0.05cm},\hspace{0.2cm} z_0 = x_0 + {\rm j} \cdot y_0\hspace{0.05cm}.\]
Die Grafik zeigt das Rice–Fading–Kanalmodell. Als Sonderfall ergibt sich daraus wieder das Rayleigh–Modell, wenn man x0 = y0 = 0 setzt.
Das Rice–Fading–Modell lässt sich wie folgt zusammenfassen:
- Der Realteil x(t) ist gaußverteilt (Mittelwert x0, und Varianz σ2). Der Imaginärteil y(t) ist ebenfalls gaußverteilt (Mittelwert y0, Varianz σ2) sowie unabhängig von x(t).
- Für z0 ≠ 0 ist der Betrag |z(t)| riceverteilt, woraus die Bezeichnung „Rice–Fading” herrührt. Zur Vereinfachung der Schreibweise setzen wir |z(t)| = a(t). Für a ≤ 0 ist die Betrags–WDF fa(a) identisch 0, für a ≥ 0 gilt folgende Gleichung für die Rice–WDF:
- \[f_a(a) = \frac{a}{\sigma^2} \cdot {\rm exp} [ -\frac{a^2 + |z_0|^2}{2\sigma^2}] \cdot {\rm I}_0 \left [ \frac{a \cdot |z_0|}{\sigma^2} \right ]\hspace{0.05cm}.\]
- Hierbei bezeichnet I0 die modifizierte Bessel–Funktion nullter Ordnung.
- \[{\rm I }_0 (u) = {\rm J }_0 ({\rm j} \cdot u) = \sum_{k = 0}^{\infty} \frac{ (u/2)^{2k}}{k! \cdot \Gamma (k+1)} \hspace{0.05cm}.\]
- Der Mobilfunkkanal ist um so besser für die Digitalsignalübertragung geeignet, je größer die „Direktpfadleistung” (|z0|2) gegenüber den Leistungen der Streukomponenten (2σ2) ist.
- Ist |z0| >> σ (Faktor 3 oder mehr), so kann die Rice–WDF mit guter Näherung durch eine Gaußverteilung mit dem Mittelwert |z0| und der Streuung σ angenähert werden.
- Im Gegensatz zu Rayleigh (mit z0 = 0) ist die Phase bei Rice–Fading nicht gleichverteilt, sondern es gibt eine Vorzugsrichtung ϕ0 = arctan(y0/x0). Oft setzt man <nobr>y0 = 0</nobr> ⇒ ϕ0 = 0.
Beispielhafte Signalverläufe bei Rice–Fading (1)
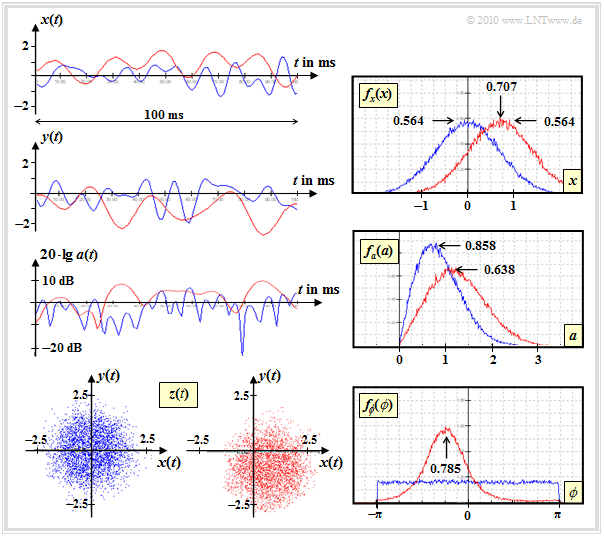
Die Grafik zeigt Signalverläufe und Dichtefunktionen zweier Mobilfunkkanäle:
- Rayleigh–Fading mit E[|z(t)|2] = 2σ2 = 1 (blaue Kurven),
- Rice–Fading mit gleichem σ sowie x0 = 0.707 und y0 = –0.707 (rote Kurven).
Für die Erzeugung der Signalausschnitte mit dem auf der letzten Seite gezeigten Modell wurde in beiden Fällen die maximale Dopplerfrequenz <nobr>fD, max = 100 Hz</nobr> zugrundegelegt. AKF und LDS von Rayleigh– und Rice–Fading unterscheiden sich nur geringfügig. Es gilt:
\[\varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.1cm} = \hspace{-0.1cm} \varphi_z ({\rm \Delta}t)\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} + |z_0|^2 \hspace{0.05cm},\] \[ {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rice}} \hspace{-0.1cm} = \hspace{-0.1cm} {\it \Phi}_z(f_{\rm D})\Bigg |_{\hspace{0.1cm}{\rm Rayleigh}} + |z_0|^2 \cdot \delta (f_{\rm D}) \hspace{0.05cm}.\]
Berücksichtigt ist, dass die Spektraldarstellung eines Gleichanteils zu einer Diracfunktion führt.
Die Bildbeschreibung folgt auf der nächsten Seite.