Difference between revisions of "Signal Representation/Discrete Fourier Transform (DFT)"
| Line 109: | Line 109: | ||
*Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt: | *Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt: | ||
| − | $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} | + | :$${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} |
{\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$ | {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$ | ||
| Line 123: | Line 123: | ||
==Von der kontinuierlichen zur diskreten Fouriertransformation== | ==Von der kontinuierlichen zur diskreten Fouriertransformation== | ||
| − | Aus dem herkömmlichen ersten Fourierintegral | + | Aus dem herkömmlichen [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|ersten Fourierintegral]] |
$$X(f) =\int_{-\infty | $$X(f) =\int_{-\infty | ||
}^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$ | }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$ | ||
| − | entsteht durch Diskretisierung ($\text{d}t \to | + | entsteht durch Diskretisierung ($\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N$) die Summe |
$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} | $${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} | ||
| Line 135: | Line 135: | ||
Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind. Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor: | Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind. Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor: | ||
| − | *Die $N$ '''Zeitbereichskoeffizienten''' seien mit der Laufvariablen $ | + | *Die $N$ '''Zeitbereichskoeffizienten''' seien mit der Laufvariablen $\nu$ = 0, ... , $N - 1$: |
$$d(\nu) = | $$d(\nu) = | ||
{\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$ | {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$ | ||
Revision as of 14:04, 8 January 2017
Contents
- 1 Argumente für die diskrete Realisierung der FT
- 2 Zeitdiskretisierung - Periodifizierung im Frequenzbereich
- 3 Frequenzdiskretisierung - Periodifizierung im Zeitbereich
- 4 Finite Signaldarstellung
- 5 Von der kontinuierlichen zur diskreten Fouriertransformation
- 6 Inverse Diskrete Fouriertransformation
- 7 Interpretation von DFT und IDFT
- 8 Aufgaben zum Kapitel
Argumente für die diskrete Realisierung der FT
Die Fouriertransformation gemäß der bisherigen Beschreibung im Kapitel Aperiodische Signale - Impulse weist aufgrund der unbegrenzten Ausdehnung des Integrationsintervalls eine unendlich hohe Selektivität auf und ist deshalb ein ideales theoretisches Hilfsmittel der Spektralanalyse. Sollen die Spektralanteile $X(f)$ einer Zeitfunktion $x(t)$ numerisch ermittelt werden, so sind die allgemeinen Transformationsgleichungen
$$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\boldsymbol {\rm Hintransformation}} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} {\boldsymbol {\rm R\ddot{u}cktransformation}} \hspace{0.05cm}\end{align*}$$
aus zwei Gründen ungeeignet:
- Die Gleichungen gelten ausschließlich für zeitkontinuierliche Signale. Mit Digitalrechnern oder Signalprozessoren können jedoch nur zeitdiskrete Signale verarbeitet werden.
- Für eine numerische Auswertung der beiden Fourierintegrale ist es erforderlich, das jeweilige Integrationsintervall auf einen endlichen Wert zu begrenzen.
Daraus ergibt sich folgende Konsequenz: Ein kontinuierliches Signal muss vor der numerischen Bestimmung seiner Spektraleigenschaften zwei Prozesse durchlaufen, nämlich
- den der Abtastung zur Diskretisierung, und
- den der Fensterung zur Begrenzung des Integrationsintervalls.
Im Folgenden wird ausgehend von einer aperiodischen Zeitfunktion $x(t)$ und dem dazugehörigen Fourierspektrum $X(f)$ eine für die Rechnerverarbeitung geeignete zeit– und frequenzdiskrete Beschreibung schrittweise entwickelt.
Zeitdiskretisierung - Periodifizierung im Frequenzbereich
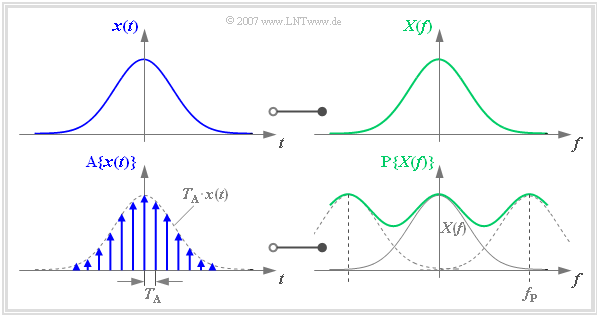
Die folgenden Grafiken zeigen einheitlich links den Zeitbereich und rechts den Frequenzbereich. Ohne Einschränkung der Allgemeingültigkeit sind $x(t)$ und $X(f)$ jeweils reell und gaußförmig.
Entsprechend dem Kapitel Zeitdiskrete Signaldarstellung kann man die Abtastung des Zeitsignals $x(t)$ durch die Multiplikation mit einem Diracpuls $p_{\delta}(t)$ beschreiben. Es ergibt sich das im Abstand $T_{\rm A}$ abgetastete Zeitsignal
$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$
Das abgetastete Signal $\text{A}\{ x(t)\}$ transformieren wir nun in den Frequenzbereich. Der Multiplikation des Diracpulses $p_{\delta}(t)$ mit $x(t)$ entspricht im Frequenzbereich die Faltung von $P_{\delta}(f)$ mit $X(f)$. Es ergibt sich das periodifizierte Spektrum $\text{P}\{ X(f)\}$, wobei $f_{\rm P}$ die Frequenzperiode der Funktion $\text{P}\{ X(f)\}$ angibt:
$${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} )\hspace{0.5cm} {\rm mit }\hspace{0.5cm}f_{\rm P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$
Dieser Zusammenhang wurde ebenfalls bereits im Kapitel Zeitdiskrete Signaldarstellung hergeleitet, jedoch mit etwas anderer Nomenklatur. Diese Nomenklaturänderung wird auf den nachfolgenden Seiten begründet:
- Das abgetastete Signal $\text{A}\{ x(t)\}$ anstelle von $x_{\rm A}(t)$.
- Die Frequenzperiode $f_{\rm P}$ = $1/T_{\rm A}$ anstelle von $f_{\rm A} = 1/T_{\rm A}$.
Die Grafik zeigt den hier beschriebenen Funktionalzusammenhang. Hierzu ist anzumerken:
- Die Frequenzperiode $f_{\rm P}$ wurde hier aus Darstellungsgründen bewusst klein gewählt, so dass die Überlappung der zu summierenden Spektren deutlich zu erkennen ist.
- In der Praxis sollte $f_{\rm P}$ aufgrund des Abtasttheorems mindestens doppelt so groß sein wie die größte im Signal $x(t)$ enthaltene Frequenz.
- Ist dies nicht erfüllt, so muss mit Aliasing gerechnet werden – siehe Kapitel Fehlermöglichkeiten bei Anwendung der DFT.
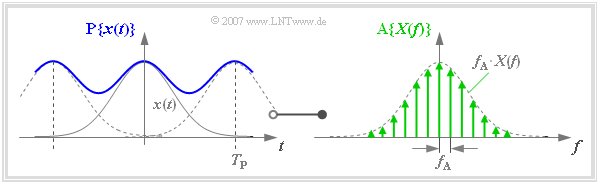
Frequenzdiskretisierung - Periodifizierung im Zeitbereich
Die Diskretisierung von $X(f)$ lässt sich ebenfalls durch eine Multiplikation mit einem Diracpuls beschreiben. Es ergibt sich das im Abstand $f_{\rm A}$ abgetastete Spektrum:
$${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$
Transformiert man den hier verwendeten Frequenz–Diracpuls (mit Impulsgewichten $f_{\rm A}$) in den Zeitbereich, so erhält man mit $T_{\rm P} = 1/f_{\rm A}$:
$$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
Die Multiplikation mit $X(f)$ entspricht im Zeitbereich der Faltung mit $x(t)$. Man erhält das im Abstand $T_{\rm P}$ periodifizierte Signal $\text{P}\{ x(t)\}$:
$${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$
Dieser Zusammenhang ist in der Grafik veranschaulicht. Aufgrund der groben Frequenzrasterung ergibt sich in diesem Beispiel für die Zeitperiode $T_{\rm P}$ ein relativ kleiner Wert, so dass sich das periodifizierte Zeitsignal $\text{P}\{ x(t)\}$ aufgrund von Überlappungen deutlich von $x(t)$ unterscheidet.
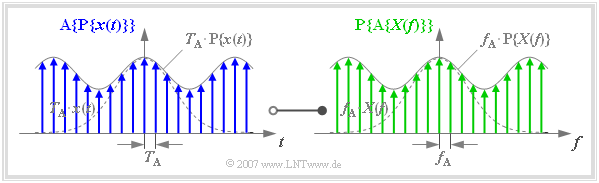
Finite Signaldarstellung
Zur finiten Signaldarstellung kommt man, wenn sowohl die Zeitfunktion $x(t)$ wie auch die Spektralfunktion $X(f)$ ausschließlich durch ihre Abtastwerte angegeben werden.
Diese Grafik ist wie folgt zu interpretieren:
- Im linken Bild blau eingezeichnet ist die Funktion $\text{A}\{ \text{P}\{ x(t)\}\}$. Diese ergibt sich durch Abtastung der periodifizierten Zeitfunktion $\text{P}\{ x(t)\}$ mit äquidistanten Diracimpulsen im Abstand $T_{\rm A} = 1/f_{\rm P}$.
- Im rechten Bild grün eingezeichnet ist die Funktion $\text{P}\{ \text{A}\{ X(f)\}\}$. Diese ergibt sich durch Periodifizierung (mit $f_{\rm P}$) der abgetasteten Spektralfunktion $\{ \text{A}\{ X(f)\}\}$.
- Zwischen dem blauen finiten Signal und dem grünen finiten Signal besteht eine Fourierkorrespondenz:
- $${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$
- Die Diraclinien der periodischen Fortsetzung $\text{P}\{ \text{A}\{ X(f)\}\}$ der abgetasteten Spektralfunktion fallen allerdings nur dann in das gleiche Frequenzraster wie diejenigen von $\text{A}\{ X(f)\}$, wenn die Frequenzperiode $f_{\rm P}$ ein ganzzahliges Vielfaches ($N$) des Frequenzabtastabstandes $f_{\rm A}$ ist.
- Deshalb muss bei Anwendung der finiten Signaldarstellung stets gelten, wobei für die natürliche Zahl $N$ in der Praxis meist eine Zweierpotenz verwendet wird (der obigen Grafik liegt der Wert $N = 8$ zugrunde):
- $$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A}}= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$
- Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt:
- $${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$
Die Zeitfunktion $\text{P}\{ \text{A}\{ x(t)\}\}$} besitzt die Periode $T_{\rm P} = N \cdot T_{\rm A}$ und die Periode im Frequenzbereich ist $f_{\rm P} = N \cdot f_{\rm A}$. Zur Beschreibung des diskretisierten Zeit– und Frequenzverlaufs reichen somit jeweils $N$ komplexe Zahlenwerte in Form von Impulsgewichten aus.
Es liegt ein impulsartiges Signal $x(t)$ in abgetasteter Form vor, wobei der Abstand zweier Abtastwerte $T_{\rm A} = 1\,\text{μs}$ beträgt. Nach einer diskreten Fouriertransformation mit $N$ = 512 liegt das Spektrum $X(f)$ in Form von Abtastwerten im Abstand $f_{\rm A} = (N \cdot T_{\rm A})^{–1} \approx 1.953\,\text{kHz} $ vor. Vergrößert man $N$ auf 2048, so ergibt sich ein feineres Frequenzraster mit $f_{\rm A} \approx 488\,\text{Hz}$.
Von der kontinuierlichen zur diskreten Fouriertransformation
Aus dem herkömmlichen ersten Fourierintegral
$$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$
entsteht durch Diskretisierung ($\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N$) die Summe
$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$
Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind. Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor:
- Die $N$ Zeitbereichskoeffizienten seien mit der Laufvariablen $\nu$ = 0, ... , $N - 1$:
$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$
- Die $N$ Frequenzbereichskoeffizienten seien mit der Laufvariablen $\mu$ = 0, ... , $N$ – 1:
$$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$
- Abkürzend wird für den komplexen Drehfaktor – der von $N$ abhängt – geschrieben:
$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
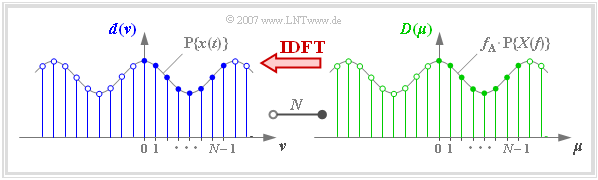
Die Gleichung der Diskreten Fouriertransformation (kurz DFT) lautet:
$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$
Oder in Worten: Unter dem Begriff Diskrete Fouriertransformation versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(ν)$.
In der Grafik erkennt man die $N$ = 8 Signalkoeffizienten d$(ν)$ an der blauen Füllung und die $N$ = 8 Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.
Inverse Diskrete Fouriertransformation
Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das zweite Fourierintegral
$$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$
in diskretisierter Form. Man erhält mit dem Übergang $\text{d}f \to f_A$:
$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm},\hspace{1.55cm} \nu = 0, ... \hspace{0.05cm}, N-1\hspace{0.05cm},$$
Die Gleichung der Inversen Diskreten Fouriertransformation (kurz IDFT) lautet:
$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
In anderen Worten: Unter dem Begriff Inverse Diskrete Fouriertransformation versteht man die Berechnung der Signalkoeffizienten $d(ν)$ aus den Spektralkoeffizienten $D(\mu)$.
Es gelten auch hier die Definitionen:
$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm},\hspace{1.55cm} \nu = 0, ... \hspace{0.05cm}, N-1\hspace{0.05cm},$$
$$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}} \hspace{0.05cm},\hspace{0.3cm} \mu = 0, ... \hspace{0.05cm}, N-1\hspace{0.05cm},$$
$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.05cm}.$$
Ein Vergleich zwischen der DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind:
- Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen.
- Bei der IDFT entfällt die Division durch $N$.
Interpretation von DFT und IDFT
Die folgende Grafik zeigt nochmals die diskreten Koeffizienten im Zeit– und Frequenzbereich zusammen mit den periodifizierten zeitkontinuierlichen Funktionen.
Bei Anwendung von DFT bzw. IDFT ist zu beachten:
- Nach obigen Definitionen besitzen die DFT–Koeffizienten $d(ν)$ und $D(\mu)$ stets die Einheit der Zeitfunktion. Dividiert man $D(\mu)$ durch $f_A$, so erhält man den Spektralwert $X(\mu \cdot f_A)$.
- Die Spektralkoeffizienten $D(\mu)$ müssen stets komplex angesetzt werden, um auch ungerade Zeitfunktionen berücksichtigen zu können.
- Aus Symmetriegründen verwendet man meist komplexe Zeitkoeffizienten $d(ν)$, um auch Bandpass–Signale im äquivalenten Tiefpassbereich transformieren zu können.
- Als Grundintervall für $ν$ $\mu$ definiert man meist – wie in obiger Grafik – den Bereich von 0 bis $N$ – 1. Mit den komplexwertigen Zahlenfolgen
$$\langle d(\nu)\rangle = \langle d(0), ... , d(N-1) \rangle \hspace{0.2cm}{\rm sowie}\hspace{0.2cm} \langle D(\mu)\rangle = \langle D(0), ... , D(N-1) \rangle$$ werden DFT und IDFT ähnlich wie die herkömmliche Fouriertransformation symbolisiert: $$\langle D(\mu)\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle d(\nu)\rangle \hspace{0.05cm}.$$
- Ist die Zeitfunktion $x(t)$ bereits auf den Bereich 0 ≤ $t$ < $N \cdot T_A$ begrenzt, dann geben die Zeitkoeffizienten direkt die Abtastwerte der Zeitfunktion an ⇒ $d(ν) = x(ν \cdot T)$.
- Ist das Zeitsignal $x(t)$ gegenüber dem Grundintervall verschoben, so muss man die auf der nächsten Seite gezeigte Zuordnung zwischen $x(t)$ und den Koeffizienten $d(ν)$ wählen.
Die obere Grafik zeigt den unsymmetrischen Dreieckimpuls $x(t)$, dessen absolute Breite kleiner ist als $T_P = N \cdot T_A$.
Die untere Skizze zeigt die zugeordneten DFT–Koeffizienten für das Beispiel $N$ = 8.
Für die Zeitindizes $ν = 0$, ... , $N/2 = 4$ gilt $d(ν) = x(ν \cdot T_A)$.
Dagegen sind die Koeffizienten $d$(5), $d$6) und $d$(7) wie folgt zu setzen:
Aufgaben zum Kapitel
Z5.2 DFT eines Dreieckimpulses