Difference between revisions of "Signal Representation/Possible Errors when using DFT"
| Line 46: | Line 46: | ||
| − | ==DFT - Verfälschung durch Fensterung - Abbruchfehler== | + | ==DFT-Verfälschung durch Fensterung - Abbruchfehler== |
Ein typischer Fehler bei Anwendung der DFT ist auf die '''Fensterung''' zurückzuführen. Diese als ''Abbruchfehler'' bekannte Verfälschung lässt sich folgendermaßen erklären: | Ein typischer Fehler bei Anwendung der DFT ist auf die '''Fensterung''' zurückzuführen. Diese als ''Abbruchfehler'' bekannte Verfälschung lässt sich folgendermaßen erklären: | ||
| Line 75: | Line 75: | ||
| − | ==DFT - Verfälschung durch Abtastung - Aliasingfehler== | + | ==DFT-Verfälschung durch Abtastung - Aliasingfehler== |
Auch durch eine ungeeignete Abtastung der Zeitfunktion $x(t)$ kann es zu einer Verfälschung des DFT–Ergebnisses kommen. Dieser so genannte Aliasingfehler lässt sich wie folgt erklären: | Auch durch eine ungeeignete Abtastung der Zeitfunktion $x(t)$ kann es zu einer Verfälschung des DFT–Ergebnisses kommen. Dieser so genannte Aliasingfehler lässt sich wie folgt erklären: | ||
Revision as of 18:29, 11 January 2017
Contents
Der mittlere quadratische Fehler als Qualitätskriterium
Im Folgenden werden einige Fehlermöglichkeiten bei Anwendung der DFT kurz diskutiert, wobei wir uns auf die Transformation vom Zeit– in den Frequenzbereich beschränken. Auch in seinen Abtastwerten wird sich im Allgemeinen das über die DFT ermittelte Spektrum $D(\mu )/f_{\rm A}$ vom tatsächlichen Spektrum $X(\mu \cdot f_{\rm A})$ unterscheiden, was auf zwei Prozesse zurückzuführen ist:
- die Abtastung, also die Reduzierung der Information über $x(t)$ auf $N$ Zahlenwerte,
- die Fensterung, die das Signal $x(t)$ eventuell fälschlicherweise begrenzt.
Ein Gütekriterium, das beide Fehlerarten berücksichtigt, ist der mittlere quadratische Fehler:
$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
Dieser ist stets ungleich 0. Die Größe von MQF hängt von folgenden Parametern ab:
- den Eigenschaften der vorliegenden Zeitfunktion $x(t)$ bzw. des Spektrums $X(f)$,
- dem DFT–Parameter $N$; je größer $N$ gewählt wird, umso kleiner wird MQF,
- einem der vier weiteren DFT–Parameter, zum Beispiel $f_{\rm A}$. Die weiteren Parameter sind über die Gleichungen $f_{\rm P} = N \cdot f_{\rm A}, T_{\rm P} = 1/f_{\rm A}$ und $T_{\rm A} = T_{\rm P}/N$ festgelegt.
Wir weisen Sie bereits hier auf das Lernvideo Fehlermöglichkeiten bei Anwendung der DFT hin, das den Inhalt dieses Kapitels verdeutlicht.
Wir betrachten beispielhaft einen Gaußimpuls mit der äquivalenten Impulsdauer $\Delta t = T$ ($T$ ist lediglich ein Normierungsparameter):
$$x(t) = {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm}.$$
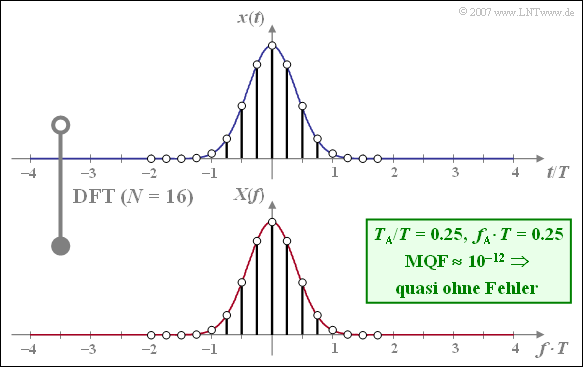
Der Gaußimpuls eignet sich aufgrund des schnellen, exponentiellen Abklingens sowohl im Zeit– als auch im Frequenzbereich sehr gut für die Anwendung der DFT. Die folgende Grafik zeigt das Ergebnis der DFT für $N = 16$ und $T_{\rm A}/T = 0.25$. Damit gilt auch: $f_{\rm A} \cdot T = 0.25$.
Zu dieser Darstellung ist Folgendes anzumerken:
- Die berücksichtigten Abtastwerte von $x(t)$ liegen im Bereich $|t/T| ≤ 2$. Da $x(\pm 2T)$ sehr klein ist, führt die Periodifizierung im Zeitbereich mit $T_{\rm P}/T = N \cdot T_{\rm A}/T = 2$ zu keinen gravierenden Fehlern.
- Mit $f_{\rm A} \cdot T = 0.25$ sowie $N = 16$ ergibt sich der (normierte) DFT–Parameter $f_{\rm P} \cdot T = 4$. Die diskreten Spektrallinien der DFT liegen somit im Bereich $–2/T ≤ f < +2/T$.
- Der mittlere quadratrische Fehler ist mit $\text{MQF} \approx 10^{–12}$ relativ klein, was auf die günstige Wahl von $f_{\rm A} \cdot T = 0.25$ (bei gegebenem $N = 16$) zurückzuführen ist.
- Die DFT–Genauigkeit kann durch Vergrößerung von $N$ verbessert werden. Für $N = 1024$ erhält man den kleinstmöglichen Wert $\text{MQF} \approx 8 \cdot 10^{–17}$, wenn $f_{\rm A} \cdot T = 0.125$ gewählt wird. Für die drei weiteren DFT–Parameter gilt dann:
- $$f_{\rm P} \cdot T = 128, \hspace{0.5cm}T_{\rm A}/T = 1/128, \hspace{0.5cm} T_{\rm P}/T = N \cdot T_{\rm A}/T= 8.$$
DFT-Verfälschung durch Fensterung - Abbruchfehler
Ein typischer Fehler bei Anwendung der DFT ist auf die Fensterung zurückzuführen. Diese als Abbruchfehler bekannte Verfälschung lässt sich folgendermaßen erklären:
- Die im DFT–Algorithmus impliziert enthaltene Fensterung entspricht der Multiplikation des Signals $x(t)$ mit einer Rechteckfunktion der Höhe 1 und der Dauer $T_{\rm P} = N \cdot T_{\rm A}$.
- Ist das Zeitsignal $x(t)$ nicht auf $T_{\rm P}$ begrenzt, so stimmt das DFT–Ergebnis nicht mit dem tatsächlichen Spektrum $X(f)$ überein, sondern ergibt sich aus diesem durch Faltung mit der Spektralfunktion $T_{\rm P} \cdot \text{si}(\pi fT_{\rm P})$.
- Im Grenzfall $T_{\rm P} \to \infty$, was bei gegebenem Abstand $T_{\rm A}$ der Abtastwerte auch eine unendlich große Stützstellenzahl $N$ bedeuten würde, entartet $T_{\rm P} \cdot \text{si}(\pi fT_{\rm P})$ zu einer Diracfunktion und das Originalspektrum $X(f)$ bliebe erhalten.
- Die DFT eines zeitlich unbegrenzten Signals – zum Beispiel eines periodischen Signals – wird immer einen Abbruchfehler hervorrufen, der nur durch besondere Maßnahmen in Grenzen gehalten werden kann. Hierauf wird in Kapitel Signaldarstellung/Spektralanalyse noch näher eingegangen.
- Bei zeitlich begrenzten, impulsartigen Signalen lässt sich der Abbruchfehler vermeiden, wenn man $T_{\rm P}$ hinreichend groß wählt. Durch weitere Vergrößerung des Fensters in Bereiche mit $x(t) \approx 0$ ergibt sich kein zusätzlicher Informationsgewinn ⇒ MQF wird nicht kleiner.
- Durch dieses Anfügen von Nullen (zero–padding) treten nun die Abtastwerte von $X(f)$ in kleinerem Abstand $f_{\rm A} = 1/T_{\rm A}$ auf. Durch $T_{\rm P}$–Verdopplung erreicht man eine Interpolation der Frequenzabtastwerte genau in der Mitte zwischen zwei vorherigen Stützstellen.
Das folgende Beispiel zeigt einen Abbruchfehler aufgrund ungünstig gewählter DFT–Parameter.
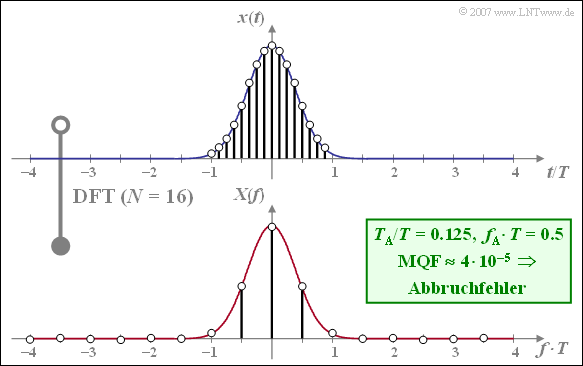
Die Grafik zeigt das Ergebnis der DFT für gleiches $x(t)$ und $X(f)$ wie auf der letzten Seite, aber nun mit den DFT–Parametern $N = 16$ und $T_{\rm A}/T = 0.125$.
Aus dem Vergleich mit der vorherigen Grafik (gültig für $T_{\rm A}/T = 0.25$) erkennt man:
- Die Frequenzabtastwerte treten nun mit doppelt so großem Abstand auf: $f_{\rm A} \cdot T = 0.5$.
- Gleichzeitig verringert sich $T_{\rm P}/T$ von $4$ auf $2$.
- Damit werden nun nur noch die Signalanteile im Bereich $|t| < T$ durch die DFT erfasst.
Mit diesen DFT–Parametern entsteht ein Abbruchfehler, durch den der mittlere quadratische Fehler (MQF) signifikant von $10^{–12}$ auf $4 \cdot 10^{–5}$ vergrößert wird.
DFT-Verfälschung durch Abtastung - Aliasingfehler
Auch durch eine ungeeignete Abtastung der Zeitfunktion $x(t)$ kann es zu einer Verfälschung des DFT–Ergebnisses kommen. Dieser so genannte Aliasingfehler lässt sich wie folgt erklären:
- Die Abtastung von $x(t)$ im Abstand $T_{\rm A}$ bewirkt eine periodische Fortsetzung des Spektrums bei ganzzahligen Vielfachen der Periodisierungsfrequenz $f_{\rm P} = 1/T_{\rm A}$.
- Besitzt das Spektrum $X(f)$ auch Spektralanteile bei $|f| > f_{\rm P}/2$, so ist das Abtasttheorem nicht erfüllt und es kommt zu Überlappungen der zu addierenden, verschobenen Frequenzanteile.
- Nur bei bandbegrenztem Signal kann der Aliasingfehler durch geeignete DFT–Parameter vermieden werden. Dagegen ist bei zeitlich begrenzten, impulsartigen Signalen dieser Fehler unvermeidbar, da zeitbegrenzte Signale nicht gleichzeitig bandbegrenzt sein können.
- Der Aliasingfehler wird durch eine feinere Abtastung (also: kleineres $T_{\rm A} = 1/f_{\rm P}$) kleiner. Dies erreicht man bei gleichbleibendem $T_{\rm A}$ – um den Abbruchfehler nicht anwachsen zu lassen – allerdings nur durch ein größeres $N$ und damit einen größeren Rechenaufwand.
Wir weisen Sie nochmals auf unser Lernvideo Fehlermöglichkeiten bei Anwendung der DFT hin.
Das folgenmde Beispiel zeigt einen solchen Aliasingfehler aufgrund falsch gewählter DFT–Parameter ($T_{\rm A}$ zu groß, $f_{\rm A}$ zu klein).
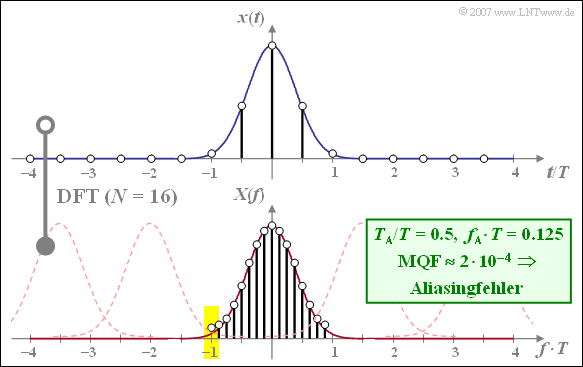
Die folgende Grafik verdeutlicht den Aliasingfehler bei gaußförmigem $x(t)$ bzw. $X(f)$. Es gelten die DFT–Parameter $N = 16$ und $f_{\rm A} \cdot T= 0.125$. Vergleichen Sie das DFT–Ergebnis mit der Grafik bei günstigerer Frequenzauflösung ($f_{\rm A} \cdot T = 0.25$, ebenfalls für $N = 16$) ⇒ „Vergleichssystem”.
Mit $N = 16$ und $f_{\rm A} \cdot T = 0.125$ gilt für die drei weiterten DFT–Parametern:
- $T_{\rm P}/T = 8$ (beim Vergleichssystem: $T_{\rm P}/T = 4$),
- $f_{\rm P} \cdot T = 2$ (beim Vergleichssystem: $f_{\rm P} \cdot T = 4$),
- $T_{\rm A}/T = 0.5$ (beim Vergleichssystem: $T_{\rm A}/T = 0.25$).
Daraus ergeben sich folgende Konsequenzen:
- Der Abbruchfehler spielt wegen $T_{\rm P} /T = 8$ keine Rolle (schon $T_{\rm P} /T = 4$ war ausreichend).
- Wegen $f_{\rm P} \cdot T = 2$ entsteht nun allerdings Aliasing, weil die DFT von der Summe vieler Gaußfunktionen im Abstand $f_{\rm P} \cdot T = 2$ ausgeht (gestrichelten Kurven in der Grafik ).
- Somit ergibt sich hier mit $\text{MQF} \approx 2 \cdot 10^{-4}$ ein noch größerer Fehlerwert als durch den Abbruchfehler im letzten Beispiel.
Die einzelnen DFT–Koeffizienten werden unterschiedlich verfälscht:
- Der mittlere DFT–Koeffizient (für die Frequenz $f = 0$) ist nahezu richtig, während die Fehler der DFT–Koeffizienten zu den Rändern hin deutlich zunehmen.
- Der DFT–Koeffizient für $f \cdot T = –1$ ist beispielsweise doppelt so groß als er sein sollte, da die Gaußfunktion mit dem Zentrum bei $f \cdot T = –2$ den gleichen Beitrag liefert wie die eigentliche Gaußfunktion um $f \cdot T = 0$ (siehe gelbe Hinterlegung).
Aufgaben zum Kapitel
A5.3 Mittlerer Quadratischer Fehler