Difference between revisions of "Aufgaben:Exercise 1.1: Music Signals"
| Line 54: | Line 54: | ||
===Musterlösung zu „Aufgabe 1.1 Musiksignale”=== | ===Musterlösung zu „Aufgabe 1.1 Musiksignale”=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
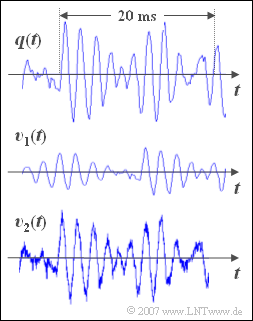
| − | '''1.''' Im markierten Bereich (20 Millisekunden) sind ca 10 Schwingungen zu erkennen. Daraus folgt für die Signalfrequenz näherungsweise | + | '''1.''' Im markierten Bereich (20 Millisekunden) sind ca 10 Schwingungen zu erkennen. Daraus folgt für die Signalfrequenz näherungsweise das Ergebnis $f = {10}/{20 \,\text{ms}} = 500 \,\text{Hz}$ ⇒ '''Lösungsvorschlag 2'''. |
| − | $f = | ||
'''2.''' Das Signal <math>v_1(t)</math> ist gegenüber dem Orginalsignal <math>q(t)</math> unverzerrt. Es gilt: | '''2.''' Das Signal <math>v_1(t)</math> ist gegenüber dem Orginalsignal <math>q(t)</math> unverzerrt. Es gilt: | ||
Revision as of 14:58, 12 January 2017
Aufgabe zu Prinzip der Nachrichtenübertragung
Nebenstehend sehen Sie einen ca. 30 ms langen Ausschnitt eines Musiksignals \(q(t)\). Es handelt sich um das Stück „Für Elise” von Ludwig van Beethoven.
Darunter gezeichnet sind zwei Sinkensignale \(v_1(t)\) und \(v_2(t)\), die nach der Übertragung des Musiksignals \(q(t)\) über zwei unterschiedliche Kanäle aufgezeichnet wurden. Mit Hilfe der nachfolgenden Buttons können Sie sich die jeweils ersten dreizehn Sekunden der drei Audiosignale \(q(t)\), \(v_1(t)\) und \(v_2(t)\) anhören.
Originalsignal \(q(t)\)
Sinkensignal \(v_1(t)\)
Sinkensignal \(v_2(t)\)
Hinweis: Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen zu „Aufgabe 1.1 Musiksignale”
Musterlösung zu „Aufgabe 1.1 Musiksignale”
2. Das Signal \(v_1(t)\) ist gegenüber dem Orginalsignal \(q(t)\) unverzerrt. Es gilt\[v_1(t)=\alpha \cdot q(t-\tau) \]
Eine Dämpfung \(\alpha\) und eine Laufzeit \(\tau\) führen nicht zu Verzerrungen, sondern das Signal ist leiser und es kommt später als das Original ⇒ Lösungsvorschlag 1.
3. Man erkennt sowohl im dargestellten Signalverlauf als auch im Audiosignal das additive Rauschen ⇒ Lösungsvorschläge 1 und 3. Der Signalrauschabstand beträgt dabei ca. 30 dB; dies ist aber aus dieser Darstellung nicht erkennbar.
4. Das Signal \(v_1(t)\) ist formgleich mit dem Originalsignal \(q(t)\) und unterscheidet sich von diesem lediglich durch den Amplitudenfaktor \(\alpha\) = 0.3 (entspricht etwa –10 dB) und die Laufzeit \(\tau\) = 10 ms.