Difference between revisions of "Aufgaben:Exercise 3.9: Convolution of Rectangle and Gaussian Pulse"
m (Text replacement - "Dirac impulse" to "Dirac delta") |
|||
| (22 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal Representation/The Convolution Theorem and Operation |
}} | }} | ||
| − | [[File:P_ID540__Sig_A_3_9_neu.png|250px|right| | + | [[File:P_ID540__Sig_A_3_9_neu.png|250px|right|frame|Convolution of rectangle $x(t)$ and Gaussian pulse $h(t)$]] |
| − | + | We consider a Gaussian low–pass with the equivalent bandwidth $\Delta f = 40 \,\text{MHz}$: | |
| − | $$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$ | + | :$$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$ |
| − | + | The corresponding impulse response is: | |
| − | $$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$ | + | :$$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$ |
| − | + | From the sketch it can be seen that the "equivalent time duration" ⇒ $\Delta t = 1/\Delta f = 25\,\text{ns}$ of the impulse response $h(t)$ can be read at the two inflection points of the Gaussian function. | |
| − | + | Three different pulse-like signals are now applied to the input of the low-pass filter: | |
| − | * | + | * a rectangular pulse $x_1(t)$ with amplitude $A_1 =1\,\text{V}$ and duration $T_1 = 20\,\text{ns}$ (red curve), |
| − | * | + | * a rectangular pulse $x_2(t)$ with amplitude $A_2 =10\,\text{V}$ and duration $T_2 = 2\,\text{ns}$ (violet curve), |
| − | * | + | * a Dirac delta $x_3(t)$ with impulse weight $2 \cdot 10^{–8}\text{ Vs}$ (green arrow). |
| − | '' | + | |
| − | * | + | |
| − | + | ||
| − | + | ||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/The_Convolution_Theorem_and_Operation|The Convolution Theorem and Operation]]. | ||
| − | $${\rm Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$ | + | *To answer the questions, you can use the complementary Gaussian error integral, which is defined as follows: |
| + | [[File:P_ID541__Sig_A_3_9Tab_neu.png|right|frame|Some values of the $\rm Q$–function]] | ||
| + | :$${\rm Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$ | ||
| − | |||
| − | + | This table gives some function values. | |
| + | <br clear=all> | ||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the signal $y_1(t) = x_1(t) \ast h(t)$. What values result at times $t = 0$ and $t = 20\,\text{ns}$ with the approximation $(2\pi )^{1/2} \approx 2.5$? |
|type="{}"} | |type="{}"} | ||
| − | $y_1(t=0)$ | + | $y_1(t=0)\ = \ $ { 0.682 3% } $\text{V}$ |
| − | $y_1(t=20\,\text{ns})$ | + | $y_1(t=20\,\text{ns})\ = \ $ { 0.158 3% } $\text{V}$ |
| − | { | + | {What are the signal values of the output signal $y_2(t) = x_2(t) \ast h(t)$ at the considered time points? |
|type="{}"} | |type="{}"} | ||
| − | $y_2(t=0)$ | + | $y_2(t=0)\ = \ $ { 0.8 3% } $\text{V}$ |
| − | $y_2(t=20 \,\text{ns})$ | + | $y_2(t=20 \,\text{ns})\ = \ $ { 0.11 3% } $\text{V}$ |
| − | { | + | {What is the value of the output signa $y_3(t) = x_3(t) \ast h(t)$ at the considered time points? Interpret the result. |
|type="{}"} | |type="{}"} | ||
| − | $y_3(t=0)$ | + | $y_3(t=0)\ = \ $ { 0.8 3% } $\text{V}$ |
| − | $y_3(t=20\, \text{ns})$ | + | $y_3(t=20\, \text{ns})\ = \ $ { 0.11 3% } $\text{V}$ |
| Line 55: | Line 61: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The convolution integral here is: |
| − | $$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$ | + | :$$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$ |
| − | + | *Here the substitution $u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$ was used. The integration limits are at: | |
| − | $$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \ | + | :$$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$ |
| − | + | *Using the complementary Gaussian error integral, it is also possible to write for this: | |
| − | $$y_1 (t) = A_1 \cdot \ | + | :$$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$ |
| − | + | *For time $t = 0$ one obtains with $(2\pi )^{1/2} \approx 2.5$: | |
| − | $$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$ | + | :$$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$ |
| − | + | *With $u_1 = -u_2 = -1$ , it follows for the two signal values we are looking for: | |
| − | $$y_1 ( {t = 0} ) \approx A_1 \cdot \ | + | :$$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$ |
| − | $$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \ | + | :$$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \big[ {{\rm Q}( 1 ) - {\rm Q}( 3 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.159 - 0}}{\rm{.001}}} \big] \hspace{0.15 cm}\underline{= 0.158\;{\rm{V}}}{\rm{.}}$$ |
| − | '''2 | + | '''(2)''' Analogous to the first sample solution, one obtains $x_2(t)$ for the narrower input pulse: |
| − | $$y_2 ( {t = 0} ) \approx A_2 \cdot \ | + | :$$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$ |
| − | $$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \ | + | :$$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \big[ {{\rm Q}( {1.9} ) - {\rm Q}( {2.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.029 - 0}}{\rm{.018}}} \big] \hspace{0.15 cm}\underline{= 0.11\;{\rm{V}}}{\rm{.}}$$ |
| − | '''3 | + | '''(3)''' With the Dirac delta $x_3(t)$ , the output signal $y_3(t)$ is equal to the impulse response $h(t)$, weighted by the weight of the Dirac function: |
| − | $$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$ | + | :$$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$ |
| + | |||
| + | *At time $t = 0$ , one also obtains here with a good approximation $y_3( t=0)\hspace{0.15 cm}\underline{ =0.8\, {\rm V}}$. | ||
| + | *After $20\, \rm ns$ , the output pulse is smaller by a factor of ${\rm e}^{–0.64π} \hspace{0.15 cm}\underline{\approx 0.136}$ and one obtains $y_3( t = 20 \,\text{ns}) ≈ 0.11 \,\text{V}$. | ||
| − | |||
| − | |||
| − | + | One can see from comparing the results from '''(2)''' and '''(3)''', that $y_3(t) \approx y_2(t)$ gilt. | |
| − | * | + | *The reason for this is that the Dirac delta is a good approximation for a rectangular input impulse of the same area if the rectangular duration $T$ is significantly smaller than the equivalent impulse duration $\Delta t$ of the impulse response. |
| − | * | + | *This means for our example: If the duration $T$ of the rectangular input impulse $x(t)$ is clearly smaller than the "equivalent pulse duration" $\Delta t$ of the Gaussian impulse response $h(t)$, then $y(t)$ is also almost Gaussian. But: '''Gaussian (once) folded with non–Gaussian never results in (exactly) Gaussian!''' |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.4 The Convolution Theorem^]] |
Latest revision as of 08:05, 26 May 2021
We consider a Gaussian low–pass with the equivalent bandwidth $\Delta f = 40 \,\text{MHz}$:
- $$H( f ) = {\rm{e}}^{{\rm{ - \pi }}( {f/\Delta f} )^2 } .$$
The corresponding impulse response is:
- $$h( t ) = \Delta f \cdot {\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm} \cdot \hspace{0.05cm} t} )^2 } .$$
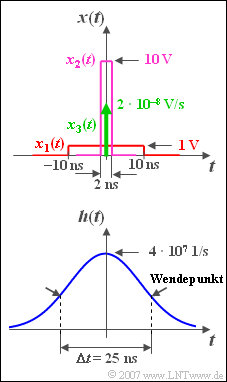
From the sketch it can be seen that the "equivalent time duration" ⇒ $\Delta t = 1/\Delta f = 25\,\text{ns}$ of the impulse response $h(t)$ can be read at the two inflection points of the Gaussian function.
Three different pulse-like signals are now applied to the input of the low-pass filter:
- a rectangular pulse $x_1(t)$ with amplitude $A_1 =1\,\text{V}$ and duration $T_1 = 20\,\text{ns}$ (red curve),
- a rectangular pulse $x_2(t)$ with amplitude $A_2 =10\,\text{V}$ and duration $T_2 = 2\,\text{ns}$ (violet curve),
- a Dirac delta $x_3(t)$ with impulse weight $2 \cdot 10^{–8}\text{ Vs}$ (green arrow).
Hints:
- This exercise belongs to the chapter The Convolution Theorem and Operation.
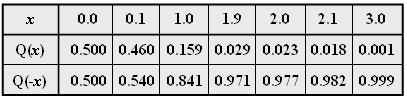
- To answer the questions, you can use the complementary Gaussian error integral, which is defined as follows:
- $${\rm Q}( x ) = \frac{1}{ {\sqrt {2{\rm{\pi }}} }}\int_{\it x}^\infty {{\rm{e}}^{{{ - {\it u}}}^{\rm{2}} {\rm{/2}}} }\hspace{0.1cm}{\rm{d}}{\it u}.$$
This table gives some function values.
Questions
Solution
- $$y_1( t ) = A_1 \cdot \Delta f \cdot \int_{t - T_1 /2}^{t + T_1 /2} {{\rm{e}}^{{\rm{ - \pi }}( {\Delta f \hspace{0.05cm}\cdot \hspace{0.05cm} \tau } )^2 } }\hspace{0.1cm} {\rm{d}}\tau = \frac{A_1 }{\sqrt{2\pi }} \cdot\int_{u_1 }^{u_2 } {{\rm{e}}^{ - u^2 /2}\hspace{0.1cm} {\rm{d}}u.}$$
- Here the substitution $u = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \tau$ was used. The integration limits are at:
- $$u_1 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t - T_1 /2} \big),\hspace{0.5cm}u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \big( {t + T_1 /2} \big).$$
- Using the complementary Gaussian error integral, it is also possible to write for this:
- $$y_1 (t) = A_1 \cdot \big[ {{\rm Q} ( {u_1 } ) - {\rm Q}( {u_2 } )} \big].$$
- For time $t = 0$ one obtains with $(2\pi )^{1/2} \approx 2.5$:
- $$u_2 = \sqrt {2{\rm{\pi }}} \cdot \Delta f \cdot \frac{ {T_1 }}{2} \approx 2.5 \cdot 4 \cdot 10^{7} \;{\rm{1/s}} \cdot 10^{-8} \;{\rm{s}} = 1.$$
- With $u_1 = -u_2 = -1$ , it follows for the two signal values we are looking for:
- $$y_1 ( {t = 0} ) \approx A_1 \cdot \big[ {{\rm Q}( { - 1} ) - {\rm Q}(+ 1 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.841 - 0}}{\rm{.159}}} \big] \hspace{0.15 cm}\underline{= 0.682\;{\rm{V}}}{\rm{,}}$$
- $$y_1 ( {t = 20\;{\rm{ns}}} ) \approx A_1 \cdot \big[ {{\rm Q}( 1 ) - {\rm Q}( 3 )} \big] = 1\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.159 - 0}}{\rm{.001}}} \big] \hspace{0.15 cm}\underline{= 0.158\;{\rm{V}}}{\rm{.}}$$
(2) Analogous to the first sample solution, one obtains $x_2(t)$ for the narrower input pulse:
- $$y_2 ( {t = 0} ) \approx A_2 \cdot \big[ {{\rm Q}( { - 0.1} ) - {\rm Q}( {0.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.540 - 0}}{\rm{.460}}} \big] \hspace{0.15 cm}\underline{= 0.80\;{\rm{V}}}{\rm{,}}$$
- $$y_2 ( {t = 20\,{\rm ns}} ) \approx A_2 \cdot \big[ {{\rm Q}( {1.9} ) - {\rm Q}( {2.1} )} \big] = 10\;{\rm{V}} \cdot \big[ {{\rm{0}}{\rm{.029 - 0}}{\rm{.018}}} \big] \hspace{0.15 cm}\underline{= 0.11\;{\rm{V}}}{\rm{.}}$$
(3) With the Dirac delta $x_3(t)$ , the output signal $y_3(t)$ is equal to the impulse response $h(t)$, weighted by the weight of the Dirac function:
- $$y_3 (t) = 2 \cdot 10^{ - 8} \,{\rm{Vs}} \cdot 4 \cdot 10^7 \;{\rm{1/s}} \cdot {\rm{e}}^{ - {\rm{\pi }}( {\Delta f \cdot t})^2 }.$$
- At time $t = 0$ , one also obtains here with a good approximation $y_3( t=0)\hspace{0.15 cm}\underline{ =0.8\, {\rm V}}$.
- After $20\, \rm ns$ , the output pulse is smaller by a factor of ${\rm e}^{–0.64π} \hspace{0.15 cm}\underline{\approx 0.136}$ and one obtains $y_3( t = 20 \,\text{ns}) ≈ 0.11 \,\text{V}$.
One can see from comparing the results from (2) and (3), that $y_3(t) \approx y_2(t)$ gilt.
- The reason for this is that the Dirac delta is a good approximation for a rectangular input impulse of the same area if the rectangular duration $T$ is significantly smaller than the equivalent impulse duration $\Delta t$ of the impulse response.
- This means for our example: If the duration $T$ of the rectangular input impulse $x(t)$ is clearly smaller than the "equivalent pulse duration" $\Delta t$ of the Gaussian impulse response $h(t)$, then $y(t)$ is also almost Gaussian. But: Gaussian (once) folded with non–Gaussian never results in (exactly) Gaussian!