Difference between revisions of "Aufgaben:Exercise 4.3: Pointer Diagram Representation"
| (27 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Analytical_Signal_and_Its_Spectral_Function |
}} | }} | ||
| − | [[File:P_ID716__Sig_A_4_3.png|250px|right| | + | [[File:P_ID716__Sig_A_4_3.png|250px|right|frame|Pointer diagram of a harmonic]] |
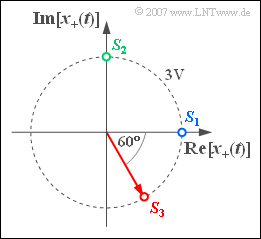
| − | + | We consider an analytical signal $x_+(t)$, which is defined by the drawn diagram in the complex plane. Depending on the choice of signal parameters, this results in three physical band-pass signals $x_1(t)$, $x_2(t)$ and $x_3(t)$, which differ by different starting points $S_i = x_i(t = 0)$. | |
| − | |||
| − | |||
| − | |||
| − | + | In addition, the angular velocities of the three constellations (blue, green and red point) are also different: | |
| − | * | + | *The (blue) analytical signal $x_{1+}(t)$ starts at $S_1 = 3 \ \rm V$. The angular velocity is $\omega_1 = \pi \cdot 10^{4} \ 1/\text{s}$. |
| − | * | + | *The signal $x_{2+}(t)$ starts at the green starting point $S_2 = {\rm j} \cdot 3 \ \text{V}$ and, compared to $x_{1+}(t)$ , rotates with twice the angular velocity ⇒ $\omega_2 = 2 \cdot \omega_1$. |
| + | *The signal $x_{3+}(t)$ starts at the red starting point $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi /3}$ and rotates with same speed as the signal $x_{2+}(t)$. | ||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/Analytical_Signal_and_Its_Spectral_Function|Analytical Signal and its Spectral Function]]. | ||
| + | *The interactive applet [[Applets:Physical_Signal_%26_Analytic_Signal|Physical and Analytical Signal]] illustrates the topic covered here. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the amplitudes of all signals considered? |
|type="{}"} | |type="{}"} | ||
| − | $A=$ { 3 } V | + | $A\ = \ $ { 3 3% } $\text{V}$ |
| − | { | + | {What are the frequency and phase values of the signal $x_1(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $f_1 =$ { 5 } kHz | + | $f_1\ = \ $ { 5 3% } $\text{kHz}$ |
| − | $\ | + | $\varphi_1\ = \ $ { 0. } $\text{deg}$ |
| − | { | + | {What are the frequency and phase values of the signal $x_2(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $f_2 = $ { 10 } kHz | + | $f_2\ = \ $ { 10 3% } $\text{kHz}$ |
| − | $\ | + | $\varphi_2\ = \ $ { -91--89 } $\text{deg}$ |
| − | { | + | {What are the frequency and phase values of the signal $x_3(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $f_3 = $ { 10 } kHz | + | $f_3\ = \ $ { 10 3% } $\text{kHz}$ |
| − | $\ | + | $\varphi_3\ = \ $ { 60 3% } $\text{deg}$ |
| − | { | + | {After what time $t_1$ is the analytical signal $x_{3+}(t)$ for the first time again equal to the initial value $x_{3+}(t = 0)$? |
|type="{}"} | |type="{}"} | ||
| − | $t_1 = $ { 0.1 3% } ms | + | $t_1\ = \ $ { 0.1 3% } $\text{ms}$ |
| − | { | + | {After what time $t_2$ is the physical signal $x_3(t)$ for the first time again as large as at time $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $t_2 = $ { 0.033 3% } ms | + | $t_2\ = \ $ { 0.033 3% } $\text{ms}$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The amplitude of the harmonic oscillation is equal to the pointer length. For all signals $A \; \underline{= 3 \ \text{V}}$. |
| + | |||
| − | '''2 | + | '''(2)''' The sought frequency is given by $f_1 = \omega_1/(2\pi ) \; \underline{= 5 \ \text{kHz}}$. |
| + | *The phase can be determined from $S_1 = 3 \ \text{V} \cdot \text{e}^{–\text{j} \hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_1}$ and is $\varphi_1 \; \underline{= 0}$. | ||
| + | *In total this gives | ||
| − | $$x_1(t) = 3\hspace{0.05cm}{\rm V} | + | :$$x_1(t) = 3\hspace{0.05cm}{\rm V} |
\cdot {\cos} ( 2 \pi \cdot {\rm 5 \hspace{0.05cm} kHz}\cdot t) .$$ | \cdot {\cos} ( 2 \pi \cdot {\rm 5 \hspace{0.05cm} kHz}\cdot t) .$$ | ||
| − | '''3 | + | |
| + | '''(3)''' Because of $\omega_2 = 2\cdot \omega_1$ , the frequency is now $f_2 = 2 \cdot f_1 \; \underline{= 10 \ \text{kHz}}$. | ||
| + | *The phase is obtained with the starting time $S_2$ at $\text{e}^{–\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\varphi_2} = \text{j}$ ⇒ $\varphi_2 \; \underline{= -\pi /2 \; (-90^{\circ})}$. | ||
| + | *Thus the time function is: | ||
| − | $$x_2(t) = 3\hspace{0.05cm}{\rm V} | + | :$$x_2(t) = 3\hspace{0.05cm}{\rm V} |
\cdot {\cos} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t + 90^\circ) = -3\hspace{0.05cm}{\rm V} | \cdot {\cos} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t + 90^\circ) = -3\hspace{0.05cm}{\rm V} | ||
\cdot {\sin} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t ).$$ | \cdot {\sin} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t ).$$ | ||
| − | + | This signal is "minus-sine", which can also be read directly from the pointer diagram: | |
| + | *The real part of $x_{2+}(t)$ at time $t = 0$ is zero. Since the pointer turns counterclockwise, the real part is negative at first. | ||
| + | *After a quarter turn, $x_2(T/4) = - 3 \ \text{V}$. | ||
| + | *If one continues to turn counterclockwise in steps of $90^\circ$, the signal values $0 \ \text{V}$, $3 \ \text{V}$ and $0 \ \text{V}$ result. | ||
| + | |||
| + | |||
| + | '''(4)''' This sub-task can be solved analogously to sub-tasks '''(2)''' and '''(3)''' : | ||
| + | :$$f_3 \; \underline{= 10 \ \text{kHz}}, \ \varphi_3 \; \underline{= 60^\circ}.$$ | ||
| + | |||
| − | ''' | + | '''(5)''' The pointer requires exactly the period $T_3 = 1/f_3 \; \underline{= 0.1 \ \text{ms}} \;(= t_1)$ for one rotation. |
| − | |||
| − | '''6 | + | '''(6)''' The analytical signal starts at $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}60^{\circ}}$. |
| + | *If the signal rotates further by $120^\circ$, exactly the same real part results. | ||
| + | *The following relationship then applies with $t_2 = t_1/3 \; \underline{= 0.033 \ \text{ms}} $ : | ||
| − | $$x_3(t = t_2) = x_3(t = 0) = 3\hspace{0.05cm}{\rm V} | + | :$$x_3(t = t_2) = x_3(t = 0) = 3\hspace{0.05cm}{\rm V} |
\cdot {\cos} ( 60^\circ) = 1.5\hspace{0.05cm}{\rm V} | \cdot {\cos} ( 60^\circ) = 1.5\hspace{0.05cm}{\rm V} | ||
.$$ | .$$ | ||
| Line 77: | Line 103: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^4.2 Analytical Signal and its Spectral Function^]] |
Latest revision as of 15:02, 6 May 2021
We consider an analytical signal $x_+(t)$, which is defined by the drawn diagram in the complex plane. Depending on the choice of signal parameters, this results in three physical band-pass signals $x_1(t)$, $x_2(t)$ and $x_3(t)$, which differ by different starting points $S_i = x_i(t = 0)$.
In addition, the angular velocities of the three constellations (blue, green and red point) are also different:
- The (blue) analytical signal $x_{1+}(t)$ starts at $S_1 = 3 \ \rm V$. The angular velocity is $\omega_1 = \pi \cdot 10^{4} \ 1/\text{s}$.
- The signal $x_{2+}(t)$ starts at the green starting point $S_2 = {\rm j} \cdot 3 \ \text{V}$ and, compared to $x_{1+}(t)$ , rotates with twice the angular velocity ⇒ $\omega_2 = 2 \cdot \omega_1$.
- The signal $x_{3+}(t)$ starts at the red starting point $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi /3}$ and rotates with same speed as the signal $x_{2+}(t)$.
Hints:
- This exercise belongs to the chapter Analytical Signal and its Spectral Function.
- The interactive applet Physical and Analytical Signal illustrates the topic covered here.
Questions
Solution
(2) The sought frequency is given by $f_1 = \omega_1/(2\pi ) \; \underline{= 5 \ \text{kHz}}$.
- The phase can be determined from $S_1 = 3 \ \text{V} \cdot \text{e}^{–\text{j} \hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_1}$ and is $\varphi_1 \; \underline{= 0}$.
- In total this gives
- $$x_1(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 5 \hspace{0.05cm} kHz}\cdot t) .$$
(3) Because of $\omega_2 = 2\cdot \omega_1$ , the frequency is now $f_2 = 2 \cdot f_1 \; \underline{= 10 \ \text{kHz}}$.
- The phase is obtained with the starting time $S_2$ at $\text{e}^{–\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\varphi_2} = \text{j}$ ⇒ $\varphi_2 \; \underline{= -\pi /2 \; (-90^{\circ})}$.
- Thus the time function is:
- $$x_2(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t + 90^\circ) = -3\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t ).$$
This signal is "minus-sine", which can also be read directly from the pointer diagram:
- The real part of $x_{2+}(t)$ at time $t = 0$ is zero. Since the pointer turns counterclockwise, the real part is negative at first.
- After a quarter turn, $x_2(T/4) = - 3 \ \text{V}$.
- If one continues to turn counterclockwise in steps of $90^\circ$, the signal values $0 \ \text{V}$, $3 \ \text{V}$ and $0 \ \text{V}$ result.
(4) This sub-task can be solved analogously to sub-tasks (2) and (3) :
- $$f_3 \; \underline{= 10 \ \text{kHz}}, \ \varphi_3 \; \underline{= 60^\circ}.$$
(5) The pointer requires exactly the period $T_3 = 1/f_3 \; \underline{= 0.1 \ \text{ms}} \;(= t_1)$ for one rotation.
(6) The analytical signal starts at $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}60^{\circ}}$.
- If the signal rotates further by $120^\circ$, exactly the same real part results.
- The following relationship then applies with $t_2 = t_1/3 \; \underline{= 0.033 \ \text{ms}} $ :
- $$x_3(t = t_2) = x_3(t = 0) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 60^\circ) = 1.5\hspace{0.05cm}{\rm V} .$$