Difference between revisions of "Aufgaben:Exercise 2.5: Distortion and Equalization"
| (42 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Linear_Distortions |
}} | }} | ||
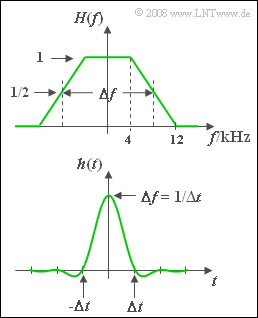
| − | [[File:P_ID907__LZI_A_2_5.png|right| | + | [[File:P_ID907__LZI_A_2_5.png|right|frame|Trapezoidal spectrum (top), <br>associated impulse response)]] |
| − | + | A communication system with input $x(t)$ and output $y(t)$, which is fully described by the trapezoidal frequency response $H(f)$ according to the top graph, is considered. Using the roll-off factor $r = 0.5$ and the equivalent bandwidth $\Delta f = 16 \ \rm kHz$ the corresponding impulse response, which is computable by applying the inverse Fourier transform, is: | |
| − | $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot | + | :$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot |
{\rm si}(\pi \cdot r \cdot \Delta f \cdot t | {\rm si}(\pi \cdot r \cdot \Delta f \cdot t | ||
| − | ) .$$ | + | ) = \Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot |
| − | + | {\rm sinc}(r \cdot \Delta f \cdot t | |
| − | + | ).$$ | |
| − | * | + | Here the following functions which can be converted into each other are used: |
| + | :$${\rm si}(x) = \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x).$$ | ||
| + | The available input signals are: | ||
| + | *The sum of two harmonic oscillations: | ||
:$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot | :$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot | ||
t).$$ | t).$$ | ||
| − | : | + | :Here, the following holds: $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$ and $\omega_2 \gt \omega_1$. |
| − | * | + | *A periodic triangular signal: |
| − | :$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \ | + | :$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) |
| − | + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}...\ | + | + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$ |
| − | : | + | :It should be noted that the basic frequency is $f_0 = 2 \ \rm kHz$ or $3\ \rm kHz$. At time $t = 0$ the signal value in both cases is $1 \ \rm V$. |
| − | * | + | *A rectangular pulse $x_3(t)$ with amplitude $A = 1 \ \rm V$ and duration $T = 1 \ \rm ms$. <br>Since its spectrum $X_3(f)$ extends to infinity, $H(f)$ always results in linear distortions here. |
| + | |||
| + | |||
| + | From subtask '''(6)''' onwards, it shall be attempted to eliminate the distortions possibly generated by $H(f)$ by means of a downstream equalizer with | ||
| + | * frequency response $H_{\rm E}(f)$, | ||
| + | * input signal $y(t)$, and | ||
| + | * output signal $z(t)$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ''Please note:'' | ||
| + | *The task belongs to the chapter [[Linear_and_Time_Invariant_Systems/Linear_Distortions|Linear Distortions]]. | ||
| + | *In particular, reference is made to the page [[Linear_and_Time_Invariant_Systems/Linear_Distortions#Equalization_methods|Equalization methods]]. | ||
| + | *The term "overall distortion" used in the formulation of the questions refers to the input signal $x(t)$ and the output signal $z(t)$. | ||
| + | |||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What types of distortion can be ruled out for this system?? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Nonlinear distortions. |
| − | - | + | - Attenuation distortions. |
| − | + | + | + Phase distortions. |
| − | { | + | {What characteristics does the system exhibit for the test signal $x_1(t)$ with $\underline{f_2 = 4 \ \rm kHz}$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It acts like an ideal system. |
| − | + | + | + It acts like a distortion-free system. |
| − | - | + | - It can be seen that the system at hand is a distorting system. |
| − | { | + | {What characteristics does the system exhibit for the test signal $x_1(t)$ with $\underline{f_2 = 10 \ \rm kHz}$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It acts like an ideal system. |
| − | - | + | - It acts like a distortion-free system. |
| − | + | + | + It can be seen that the system at hand is a distorting system. |
| − | { | + | {For the test signal $x_2(t)$ with $\underline{f_0 = 3 \ \rm kHz}$, what is the maximum deviation $\varepsilon_{\rm max} = |y_2(t_0) - x_2(t_0)|$. <br>At what time $t_0$ does $\varepsilon_{\rm max}$ occur for the first time? |
| − | |||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\varepsilon_\text{max} \ = \ $ { 0.156 3% } $\ \rm V$ |
| − | $t_0$ | + | $t_0 \ = \ $ { 0. } $\ \rm ms$ |
| − | { | + | {What is the maximum deviation $\varepsilon_{\rm max}$ with $\underline{f_0 = 2 \ \rm kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\varepsilon_\text{max} \ = \ $ { 0.114 3% } $\ \rm V$ |
| − | { | + | {What curve shape should the equalizer $H_{\rm E}(f)$ have to compensate all distortions of $H(f)$ in the best possible way? <br>What magnitude value arises as a result for $\underline{f = 10 \ \rm kHz}$? |
|type="{}"} | |type="{}"} | ||
| − | $|H_E(f = 10 kHz)|$ | + | $|H_E(f = 10 \ \rm kHz)| \ = \ $ { 4 3% } |
| − | { | + | {For which of the listed signals is complete equalization possible? <br>$z(t) = x(t)$ should be understood by "complete equalization". |
|type="[]"} | |type="[]"} | ||
| − | + | + | + For signal $x_1(t)$ with $f_2 = 10 \ \rm kHz$, |
| − | - | + | - for signal $x_2(t)$, |
| − | - | + | - for signal $x_3(t)$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' <u>Proposed solutions 1 and 3</u> are correct: | |
| + | *A linear system is already implicitly assumed by specifying a frequency response so that nonlinear distortions cannot occur. | ||
| + | *Since $H(f)$ is purely real, phase distortions can also be ruled out. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Proposed solutions 1 and 2</u> are correct: | ||
| + | *The output signal is $y_1(t) = x_1(t)$. | ||
| + | *Thus, the system is not only distortion-free but can also be termed ideal for this application. | ||
| + | |||
| + | |||
| − | + | '''(3)''' <u>Proposed solution 3</u> is correct: | |
| + | *In this case, the following is obtained for the output signal: | ||
| + | :$$y_1(t)= 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + {1}/{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$ | ||
| + | *While the component at $f_1$ is transmitted unchanged, the sinusoidal component at $f_2$ is attenuated and one-quarter of the original sinusoidal component. | ||
| + | *So, there are attenuation distortions. | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' The output signal $y_2(t)$ has the following form taking into account the basic frequency $f_0 = 3 \ \rm kHz$: | |
:$$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + | :$$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + | ||
\frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) | \frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) | ||
.$$ | .$$ | ||
| − | + | *The factor $3/8$ describes $H(f = 9 \ \rm kHz)$. All other spectral components at $15 \ \rm kHz$, $21 \ \rm kHz$, etc. are suppressed by the system. | |
| − | + | *The strongest deviations between $x_2(t)$ and $y_2(t)$ will occur at the triangle peaks since the missing high frequencies have the strongest effect here. | |
| + | *For example, for the time $\underline{t= 0}$ one obtains: | ||
:$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + | :$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + | ||
| − | + | {3}/{72}\right)= 0.844\,{\rm | |
| − | V} | + | V} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} |
| − | |||
\varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm | \varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm | ||
V}}.$$ | V}}.$$ | ||
| − | + | ||
| + | |||
| + | '''(5)''' With the basic frequency $f_0 = 2 \ \rm kHz$ and the values $H(3f_0) = 0.75$, $H(5f_0) = 0.25$, $H(7f_0) = 0$ the following is obtained: | ||
:$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + | :$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + | ||
\frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm | \frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm | ||
| Line 118: | Line 136: | ||
V}}.$$ | V}}.$$ | ||
| − | + | ||
| + | |||
| + | '''(6)''' In the range up to $4 \ \rm kHz$, $H_{\rm E}(f) = H(f) = 1$ is to be set. In contrast, in the range from $4 \ \rm kHz$ to $12 \ \rm kHz$ the following holds: | ||
:$$H_{\rm E}(f)= \frac{1}{H(f)} = | :$$H_{\rm E}(f)= \frac{1}{H(f)} = | ||
| − | \frac{1}{1.5 \cdot [1 - f/(12\,{\rm kHz})]} | + | \frac{1}{1.5 \cdot \big[1 - f/(12\,{\rm kHz})\big]} |
\hspace{0.5cm} \Rightarrow \hspace{0.5cm} | \hspace{0.5cm} \Rightarrow \hspace{0.5cm} | ||
H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} | H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} | ||
.$$ | .$$ | ||
| − | + | Here, the denominator expression describes the equation of the straight line of the frequency roll-off. | |
| + | |||
| − | |||
| − | |||
| − | + | '''(7)''' <u>Proposed solution 1</u> is correct: | |
| + | *Both $x_2(t)$ and $x_3(t)$ also contain spectral components at frequencies greater than $12 \ \rm kHz$. | ||
| + | *If these have been truncated by $H(f)$ ⇒ band limitation, they can no longer be reconstructed by the equalizer. | ||
| + | *This means that only the signal $x_1(t)$ can be recovered by $H_{\rm E}(f)$ but only if $f_2 < 12 \ \rm kHz$ holds: | ||
| + | :$$z_1(t)= \underline{1} \cdot 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + \underline{4} \cdot \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$ | ||
| + | *The first (underlined) factors indicate the gain values of $H_{\rm E}(f)$ respectively. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^2.3 Linear Distortions^]] |
Latest revision as of 15:56, 5 October 2021
A communication system with input $x(t)$ and output $y(t)$, which is fully described by the trapezoidal frequency response $H(f)$ according to the top graph, is considered. Using the roll-off factor $r = 0.5$ and the equivalent bandwidth $\Delta f = 16 \ \rm kHz$ the corresponding impulse response, which is computable by applying the inverse Fourier transform, is:
- $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t ) = \Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot {\rm sinc}(r \cdot \Delta f \cdot t ).$$
Here the following functions which can be converted into each other are used:
- $${\rm si}(x) = \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x).$$
The available input signals are:
- The sum of two harmonic oscillations:
- $$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot t).$$
- Here, the following holds: $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$ and $\omega_2 \gt \omega_1$.
- A periodic triangular signal:
- $$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$
- It should be noted that the basic frequency is $f_0 = 2 \ \rm kHz$ or $3\ \rm kHz$. At time $t = 0$ the signal value in both cases is $1 \ \rm V$.
- A rectangular pulse $x_3(t)$ with amplitude $A = 1 \ \rm V$ and duration $T = 1 \ \rm ms$.
Since its spectrum $X_3(f)$ extends to infinity, $H(f)$ always results in linear distortions here.
From subtask (6) onwards, it shall be attempted to eliminate the distortions possibly generated by $H(f)$ by means of a downstream equalizer with
- frequency response $H_{\rm E}(f)$,
- input signal $y(t)$, and
- output signal $z(t)$.
Please note:
- The task belongs to the chapter Linear Distortions.
- In particular, reference is made to the page Equalization methods.
- The term "overall distortion" used in the formulation of the questions refers to the input signal $x(t)$ and the output signal $z(t)$.
Questions
Solution
- A linear system is already implicitly assumed by specifying a frequency response so that nonlinear distortions cannot occur.
- Since $H(f)$ is purely real, phase distortions can also be ruled out.
(2) Proposed solutions 1 and 2 are correct:
- The output signal is $y_1(t) = x_1(t)$.
- Thus, the system is not only distortion-free but can also be termed ideal for this application.
(3) Proposed solution 3 is correct:
- In this case, the following is obtained for the output signal:
- $$y_1(t)= 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + {1}/{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$
- While the component at $f_1$ is transmitted unchanged, the sinusoidal component at $f_2$ is attenuated and one-quarter of the original sinusoidal component.
- So, there are attenuation distortions.
(4) The output signal $y_2(t)$ has the following form taking into account the basic frequency $f_0 = 3 \ \rm kHz$:
- $$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + \frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) .$$
- The factor $3/8$ describes $H(f = 9 \ \rm kHz)$. All other spectral components at $15 \ \rm kHz$, $21 \ \rm kHz$, etc. are suppressed by the system.
- The strongest deviations between $x_2(t)$ and $y_2(t)$ will occur at the triangle peaks since the missing high frequencies have the strongest effect here.
- For example, for the time $\underline{t= 0}$ one obtains:
- $$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + {3}/{72}\right)= 0.844\,{\rm V} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm V}}.$$
(5) With the basic frequency $f_0 = 2 \ \rm kHz$ and the values $H(3f_0) = 0.75$, $H(5f_0) = 0.25$, $H(7f_0) = 0$ the following is obtained:
- $$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + \frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm V}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\varepsilon_{\rm max} \hspace{0.15cm}\underline{= 0.114\,{\rm V}}.$$
(6) In the range up to $4 \ \rm kHz$, $H_{\rm E}(f) = H(f) = 1$ is to be set. In contrast, in the range from $4 \ \rm kHz$ to $12 \ \rm kHz$ the following holds:
- $$H_{\rm E}(f)= \frac{1}{H(f)} = \frac{1}{1.5 \cdot \big[1 - f/(12\,{\rm kHz})\big]} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} .$$
Here, the denominator expression describes the equation of the straight line of the frequency roll-off.
(7) Proposed solution 1 is correct:
- Both $x_2(t)$ and $x_3(t)$ also contain spectral components at frequencies greater than $12 \ \rm kHz$.
- If these have been truncated by $H(f)$ ⇒ band limitation, they can no longer be reconstructed by the equalizer.
- This means that only the signal $x_1(t)$ can be recovered by $H_{\rm E}(f)$ but only if $f_2 < 12 \ \rm kHz$ holds:
- $$z_1(t)= \underline{1} \cdot 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + \underline{4} \cdot \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$
- The first (underlined) factors indicate the gain values of $H_{\rm E}(f)$ respectively.