Difference between revisions of "Aufgaben:Exercise 4.1Z: Transmission Behavior of Short Cables"
| (21 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory |
}} | }} | ||
| − | [[File: | + | [[File:EN_LZI_Z_4_1.png|right|frame|Short line section]] |
| − | + | We assume a homogeneous and reflection-free terminated line of length $l$ so that the following applies to the spectral function at the output: | |
| − | $$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$ | + | :$$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$ |
| − | + | Here $\gamma(f)$ describes the '''complex propagation function''' of an extremely short line of infinitesimal length $dx$, which can be represented with the parameters $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ and $C\hspace{0.08cm}'$ (see diagram) as follows: | |
| − | $$\gamma(f) = \sqrt{(R' + {\rm j} \cdot 2\pi f \cdot L') \cdot (G' + {\rm j} \cdot 2\pi f \cdot C')} = | + | :$$\gamma(f) = \sqrt{(R\hspace{0.05cm}' + {\rm j} \cdot 2\pi f \cdot L\hspace{0.05cm}') \cdot (G\hspace{0.08cm}' + {\rm j} \cdot 2\pi f \cdot C\hspace{0.08cm}')} = |
\alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$ | \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$ | ||
| − | + | The real part of $\gamma(f)$ results in | |
| − | $$\alpha(f) = \sqrt{{1}/{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | + | *The real part of $\gamma(f)$ results in the attenuation function $\alpha(f)$ (per unit length). |
| − | {1}/{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | + | *The imaginary part of $\gamma(f)$ results in the phase function $\beta(f)$ (per unit length). |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | + | |
| + | |||
| + | After some calculation one can write for these sizes: | ||
| + | :$$\alpha(f) = \sqrt{{1}/{2}\cdot \left (R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' - \omega^2 \cdot L\hspace{0.05cm}' \cdot C\hspace{0.08cm}'\right)+ | ||
| + | {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} | ||
| + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | ||
f},$$ | f},$$ | ||
| − | $$\beta(f) = \sqrt{{1}/{2}\cdot \left (-R' G' + \omega^2 \cdot L' C'\right)+ | + | :$$\beta(f) = \sqrt{{1}/{2}\cdot \left (-R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' + \omega^2 \cdot L\hspace{0.05cm}' C\hspace{0.08cm}'\right)+ |
| − | {1}/{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | + | {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ | + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ |
| − | |||
| − | + | *For the attenuation function $a(f)$ the pseudo unit "Neper" (Np) has to be added additionally and for the phase function $b(f)$ "Radian" (rad). | |
| + | *Since the primary line parameters are each related to the line length, $\alpha(f)$ and $\beta(f)$ have the units "Np/km" and "rad/km", respectively. | ||
| − | |||
| − | |||
| − | |||
| − | '' | + | Another important descriptive quantity besides $\gamma(f)$ is the '''wave impedance''' $Z_{\rm W}(f)$, which gives the relationship between voltage and current of the two running waves at each location. It holds: |
| − | * | + | :$$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.05cm}' + {\rm j} \cdot \omega L\hspace{0.05cm}'}{G\hspace{0.08cm}' + {\rm j} \cdot \omega C\hspace{0.08cm}'}} |
| − | + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm} \omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$ | |
| − | * | + | |
| − | $$R\hspace{0. | + | |
| − | G\hspace{0. | + | |
| − | 2\pi L' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | + | |
| − | 2\pi C\hspace{0. | + | |
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory|Some Results from Line Transmission Theory]]. | ||
| + | |||
| + | *Use the following values for the numerical calculations: | ||
| + | :$$R\hspace{0.05cm}' = 100\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} | ||
| + | G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}}\hspace{0.05cm},\hspace{0.3cm} | ||
| + | 2\pi L\hspace{0.03cm}' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
| + | 2\pi C\hspace{0.08cm}' = 200\,\,{\rm nF}/{ {\rm km}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Specify $\alpha(f)$, $\beta(f)$ and $Z_{\rm W}(f)$ for frequency $f = 0$ ("direct current"). |
|type="{}"} | |type="{}"} | ||
| − | $\alpha(f = | + | $\alpha(f =0) \ =$ { 0.01 3% } $\ \rm Np/km$ |
| − | $\beta(f = | + | $\beta(f = 0) \ =$ { 0. } $\ \rm rad/km$ |
| − | $ | + | $Z_{\rm W}(f = 0) \ =$ { 10000 3% } $\ \rm \Omega$ |
| − | { | + | {Calculate the attenuation function $\alpha(f)$ (per unit length) for $f = 100\ \rm kHz$. |
|type="{}"} | |type="{}"} | ||
| − | $\alpha(f = 100\ \rm kHz) \ =$ { 0.486 3% } $\ \rm Np/km$ | + | $\alpha(f = 100\ \rm kHz) \ = \ $ { 0.486 3% } $\ \rm Np/km$ |
| − | { | + | {Give the approximations of $Z_{\rm W}(f)$ and $\alpha(f)$, valid for $f → \infty$ . |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ Z_{\rm W}(f → \infty) \ = \ $ { 100 3% } $\ \rm \Omega$ |
| − | $\alpha(f → \infty)\ =$ { 0.5 3% } $\ \rm Np/km$ | + | $\alpha(f → \infty) \ = \ $ { 0.5 3% } $\ \rm Np/km$ |
| − | { | + | {Use $\omega L\hspace{0.03cm}' \ll R\hspace{0.05cm}'$ and $\omega C\hspace{0.08cm}' \gg G\hspace{0.08cm}'$ to derive an $\alpha(f)$ approximation for (not too) small frequencies. <br>What is the attenuation function per unit length for $ f = 1 \ \rm kHz$ and $ f = 4 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | $\alpha(f = 1\ \rm kHz) \ =$ { 0.1 3% } $\ \rm Np/km$ | + | $\alpha(f = 1\ \rm kHz) \ = \ $ { 0.1 3% } $\ \rm Np/km$ |
| − | $\alpha(f = 4\ \rm kHz) \ =$ { 0.2 3% } $\ \rm Np/km$ | + | $\alpha(f = 4\ \rm kHz) \ = \ $ { 0.2 3% } $\ \rm Np/km$ |
| − | { | + | {For the same frequency range, give a suitable approximation for the wave impedance $Z_{\rm W}(f)$ . <br>What value results for $ f = 1 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re}\{ | + | ${\rm Re}\{Z_{\rm W}(f = 1\ \rm kHz)\} \ = \ $ { 500 3% } $\ \rm \Omega$ |
| − | ${\rm Im}\{ | + | ${\rm Im}\{Z_{\rm W}(f = 1\ \rm kHz)\} \ = \ $ { -515--485 } $\ \rm \Omega$ |
| Line 72: | Line 84: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' If you insert the frequency $f = 0$ into the given equations, we obtain | |
| − | :$$\alpha(f = 0) = [1\,{\rm Np}] \cdot \sqrt{ | + | :$$\alpha(f = 0) = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{{1}/{2}\hspace{-0.03cm}\cdot \hspace{-0.03cm} R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} |
| − | G'} = [1\,{\rm Np}] \cdot \sqrt{ R' \cdot G'} = | + | G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ 100\,{\rm \Omega/km} \hspace{-0.03cm}\cdot \hspace{-0.03cm} 10^{-6}\,{\rm (\Omega \hspace{-0.03cm}\cdot \hspace{-0.03cm} km})^{-1}} |
\hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} | \hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} | ||
}\hspace{0.05cm},$$ | }\hspace{0.05cm},$$ | ||
| − | :$$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{- | + | :$$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-{1}/{2}\cdot R\hspace{0.03cm}' \cdot G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \cdot |
| − | G'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$ | + | G\hspace{0.03cm}'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$ |
| − | :$$Z_{\rm W}(f = 0) = \sqrt{\frac {R'}{G'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm | + | :$$Z_{\rm W}(f = 0) = \sqrt{\frac {R\hspace{0.03cm}'}{G\hspace{0.03cm}'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm |
k \Omega}}\hspace{0.05cm}.$$ | k \Omega}}\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | The DC signal attenuation becomes relevant, | |
| + | *if the useful signal is to be transmitted in the baseband and has a DC component, or | ||
| + | *if the network termination at the participant must be supplied with power from the local exchange ("remote power supply"). | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' With $f = 10^{5} \ \rm Hz$ and the specified values, the following holds: | ||
:$$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | :$$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | ||
10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm | 10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm | ||
\Omega | \Omega | ||
| − | }{ {\rm km}} \hspace{0.05cm},\ | + | }{ {\rm km}} \hspace{0.05cm},\hspace{1.05cm} |
f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot | ||
10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 | 10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 | ||
\,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$ | \,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$ | ||
| − | + | This results in the following for the attenuation function in "Np/km": | |
| − | :$$ | + | :$$\alpha(f = 100\,{\rm kHz}) |
| − | + | = \sqrt{ {1}/{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ | |
| − | + | {1}/{2} \cdot \sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} $$ | |
| − | + | :$$ \Rightarrow \; \; \alpha(f = 100\,{\rm kHz}) \approx \sqrt{{1}/{2}\cdot \left (10^{-4} - 4 \right)+ | |
| − | + | {1}/{2}\cdot \sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ | |
| − | 2}} | + | 2}} \hspace{0.15cm}\underline{\approx 0.486 \ {\rm Np/km}} \hspace{0.05cm}.$$ |
| − | \hspace{0.15cm}\underline{\approx 0.486} \hspace{0.05cm}.$$ | ||
| − | + | ||
| + | '''(3)''' The limit for $f → \infty$ results if one neglects the second terms in the numerator $R\hspace{0.03cm}'$ and in the denominator $G\hspace{0.08cm}'$ : | ||
:$$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) | :$$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) | ||
| − | = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C'}} | + | = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C\hspace{0.03cm}'}} |
| − | =\sqrt{\frac {2 \pi L' }{2 \pi C'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } | + | =\sqrt{\frac {2 \pi L\hspace{0.03cm}' }{2 \pi C\hspace{0.03cm}'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } |
{2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$ | {2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$ | ||
| − | + | *The approximation for the attenuation function is more difficult to derive. Starting from | |
| − | :$$\alpha(\omega) = \sqrt{ | + | :$$\alpha(\omega) = \sqrt{ {1}/{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ |
| − | + | {1}/{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot C\hspace{0.03cm}\hspace{0.03cm}'^2)}}$$ | |
| − | :$$ | + | :then also the following applies: |
| + | :$$2 \cdot \alpha^2(\omega) = R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' | ||
C'\cdot | C'\cdot | ||
| − | \left [-1 +\sqrt{(1 + \frac{R'^2}{ \omega^2 \cdot L'^2}) \cdot (1 + \frac{G | + | \left [-1 +\sqrt{(1 + \frac{R\hspace{0.03cm}'^2}{ \omega^2 \cdot L\hspace{0.03cm}'^2}) \cdot (1 + \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2})} \hspace{0.1cm} |
| − | |||
| − | |||
| − | |||
| − | |||
\right]$$ | \right]$$ | ||
| − | : | + | :$$\Rightarrow \; \; 2 \cdot \alpha^2(\omega) \approx R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' |
| − | :$$2 \cdot \alpha^2(\omega \rightarrow \infty) = R' G' + \omega^2 \cdot L' | + | C\hspace{0.03cm}'\cdot |
| − | C'\cdot | + | \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2}} \hspace{0.1cm} |
| − | \left [ -1 +1 + | + | \right].$$ |
| + | *Using the approximation $\sqrt{1 + x}\approx 1+x/2$ valid for small $x$, one arrives at the intermediate result for (infinitely) large frequencies: | ||
| + | :$$2 \cdot \alpha^2(\omega \rightarrow \infty) = R\hspace{0.03cm}' G\hspace{0.05cm}' + \omega^2 \cdot L' | ||
| + | C\hspace{0.05cm}'\cdot | ||
| + | \left [ -1 +1 + {1}/{2} \cdot \left ( \frac{R\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2}+ \frac{G\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2} | ||
\right) \hspace{0.1cm} | \right) \hspace{0.1cm} | ||
| − | \right] | + | \right] $$ |
| − | G'\hspace{0.03cm}^2 L'\hspace{0.03cm}^2}{2 \cdot C' L' | + | :$$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega \rightarrow \infty) = \frac{2 \cdot R\hspace{0.03cm}' G\hspace{0.03cm}' C\hspace{0.03cm}' L'+ R\hspace{0.03cm}'\hspace{0.03cm}^2 C\hspace{0.03cm}'\hspace{0.03cm}^2+ |
| − | }= | + | G\hspace{0.03cm}'\hspace{0.03cm}^2 L\hspace{0.03cm}'\hspace{0.03cm}^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' |
| − | + | }= \frac{(R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}')^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' }$$ | |
:$$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = | :$$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = | ||
| − | + | {1}/{2}\cdot \frac{R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}'}{\sqrt{ C\hspace{0.03cm}' L\hspace{0.03cm}' }}= | |
| − | + | {1}/{2}\cdot \left [R\hspace{0.03cm}' \cdot \sqrt{\frac{C\hspace{0.03cm}'}{L\hspace{0.03cm}'}}+G\hspace{0.03cm}' \cdot \sqrt{\frac{L\hspace{0.03cm}'}{C\hspace{0.03cm}'}}\right]\hspace{0.05cm}.$$ | |
| − | + | *With the numerical values inserted, we get | |
:$$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) | :$$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) | ||
| − | = | + | = {0.5\,{\rm Np/km}}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot |
| − | |||
\sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] | \sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] | ||
\hspace{0.15cm}\underline{\approx 0.5 \, {\rm Np}/{\rm km}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{\approx 0.5 \, {\rm Np}/{\rm km}}\hspace{0.05cm}.$$ | ||
| − | + | ||
| − | :$$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R' G' - \omega^2 \cdot L' C'\right)+ | + | '''(4)''' For small frequencies, $\omega L\hspace{0.03cm}' \ll R\hspace{0.03cm}'$ and $ \omega C\hspace{0.03cm}' \gg G\hspace{0.03cm}'$ apply. |
| − | \frac {1}{2}\sqrt{(R'^2 + \omega^2 \cdot L'^2) \cdot (G'^2 + \omega^2 \cdot C'^2)}} | + | *Neglecting the $\omega^2$–part, one obtains: |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | + | :$$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ |
| − | f}\\ | + | \frac {1}{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2+ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2)}} |
| − | + | \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | |
| − | \frac {R' \cdot \omega C'}{2}} | + | f}$$ |
| − | \hspace{0.1cm}\bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | + | :$$ \Rightarrow \hspace{0.3cm} \alpha(f) \approx \sqrt{\frac {R\hspace{0.03cm}' G\hspace{0.03cm}'}{2}+ |
| + | \frac {R\hspace{0.03cm}' \cdot \omega C\hspace{0.03cm}'}{2}} | ||
| + | \hspace{0.1cm}\bigg |_{\hspace{0.03cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi | ||
f} \approx \sqrt{ | f} \approx \sqrt{ | ||
| − | + | {1}/{2} \cdot f \cdot R\hspace{0.03cm}' \cdot 2 \pi C\hspace{0.03cm}'} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Here it is considered that the first part can be neglected according to subtask '''(1)''' except for the frequency $f = 0$ . | |
| + | *For the frequency $f = 1 \ \rm kHz$ we get the approximation | ||
:$$\alpha(f = 1\,{\rm kHz}) = \sqrt{ | :$$\alpha(f = 1\,{\rm kHz}) = \sqrt{ | ||
| − | + | {1}/{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} | |
\,\frac{\rm s }{ {\rm \Omega \cdot km}}} | \,\frac{\rm s }{ {\rm \Omega \cdot km}}} | ||
\hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} | \hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *For frequency $f = 4 \ \rm kHz$ the attenuation function per unit length is twice as large: | |
:$$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} | :$$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | ||
| − | :$$Z_{\rm W}(f) = \sqrt{\frac {R' + {\rm j} \cdot f \cdot 2 \pi L'}{G' + {\rm j} \cdot f \cdot 2 \pi C'}} | + | |
| − | \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R' }{ f \cdot 2 \pi | + | '''(5)''' The wave impedance at low frequencies is approximated by: |
| − | C'}}= (1 - {\rm j})\cdot \sqrt{\frac {R' }{ 2 \cdot f \cdot 2 \pi | + | :$$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi L\hspace{0.03cm}'}{G\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi C\hspace{0.03cm}'}} |
| − | C'}}\hspace{0.05cm}.$$ | + | \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R\hspace{0.03cm}' }{ f \cdot 2 \pi |
| − | : | + | C\hspace{0.03cm}'}}= (1 - {\rm j})\cdot \sqrt{\frac {R\hspace{0.03cm}' }{ 2 \cdot f \cdot 2 \pi |
| + | C\hspace{0.03cm}'}}\hspace{0.05cm}.$$ | ||
| + | *With the specified line fittings we obtain: | ||
:$${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} | :$${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} | ||
\,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm | \,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm | ||
| − | \Omega}}\hspace{0.05cm}, | + | \Omega}}\hspace{0.05cm},$$ |
| − | + | :$$ {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm | |
\Omega}}\hspace{0.05cm}.$$ | \Omega}}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 173: | Line 195: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^4.1 Results of Line Transmission Theory^]] |
Latest revision as of 16:14, 9 November 2021
We assume a homogeneous and reflection-free terminated line of length $l$ so that the following applies to the spectral function at the output:
- $$U_2(f) = U_1(f) \cdot {\rm e}^{-\hspace{0.02cm}\gamma(f) \hspace{0.05cm} \cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
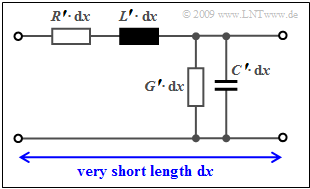
Here $\gamma(f)$ describes the complex propagation function of an extremely short line of infinitesimal length $dx$, which can be represented with the parameters $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ and $C\hspace{0.08cm}'$ (see diagram) as follows:
- $$\gamma(f) = \sqrt{(R\hspace{0.05cm}' + {\rm j} \cdot 2\pi f \cdot L\hspace{0.05cm}') \cdot (G\hspace{0.08cm}' + {\rm j} \cdot 2\pi f \cdot C\hspace{0.08cm}')} = \alpha (f) + {\rm j} \cdot \beta (f)\hspace{0.05cm}.$$
The real part of $\gamma(f)$ results in
- The real part of $\gamma(f)$ results in the attenuation function $\alpha(f)$ (per unit length).
- The imaginary part of $\gamma(f)$ results in the phase function $\beta(f)$ (per unit length).
After some calculation one can write for these sizes:
- $$\alpha(f) = \sqrt{{1}/{2}\cdot \left (R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' - \omega^2 \cdot L\hspace{0.05cm}' \cdot C\hspace{0.08cm}'\right)+ {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f},$$
- $$\beta(f) = \sqrt{{1}/{2}\cdot \left (-R\hspace{0.05cm}' \cdot G\hspace{0.08cm}' + \omega^2 \cdot L\hspace{0.05cm}' C\hspace{0.08cm}'\right)+ {1}/{2}\cdot \sqrt{(R\hspace{0.05cm}'\hspace{0.05cm}^2 + \omega^2 \cdot L\hspace{0.05cm}'\hspace{0.05cm}^2) \cdot (G\hspace{0.08cm}'\hspace{0.05cm}^2 + \omega^2 \cdot C\hspace{0.08cm}'\hspace{0.05cm}^2)}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
- For the attenuation function $a(f)$ the pseudo unit "Neper" (Np) has to be added additionally and for the phase function $b(f)$ "Radian" (rad).
- Since the primary line parameters are each related to the line length, $\alpha(f)$ and $\beta(f)$ have the units "Np/km" and "rad/km", respectively.
Another important descriptive quantity besides $\gamma(f)$ is the wave impedance $Z_{\rm W}(f)$, which gives the relationship between voltage and current of the two running waves at each location. It holds:
- $$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.05cm}' + {\rm j} \cdot \omega L\hspace{0.05cm}'}{G\hspace{0.08cm}' + {\rm j} \cdot \omega C\hspace{0.08cm}'}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm} \omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}.$$
Notes:
- The exercise belongs to the chapter Some Results from Line Transmission Theory.
- Use the following values for the numerical calculations:
- $$R\hspace{0.05cm}' = 100\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}}\hspace{0.05cm},\hspace{0.3cm} 2\pi L\hspace{0.03cm}' = 2\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} 2\pi C\hspace{0.08cm}' = 200\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
Questions
Solution
- $$\alpha(f = 0) = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{{1}/{2}\hspace{-0.03cm}\cdot \hspace{-0.03cm} R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ R\hspace{0.03cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} G\hspace{0.03cm}'} = [1\,{\rm Np}] \hspace{-0.03cm}\cdot \hspace{-0.03cm} \sqrt{ 100\,{\rm \Omega/km} \hspace{-0.03cm}\cdot \hspace{-0.03cm} 10^{-6}\,{\rm (\Omega \hspace{-0.03cm}\cdot \hspace{-0.03cm} km})^{-1}} \hspace{0.15cm}\underline{= 0.01\,{\rm Np}/{ {\rm km}} }\hspace{0.05cm},$$
- $$\beta(f = 0) = [1\,{\rm rad}] \cdot \sqrt{-{1}/{2}\cdot R\hspace{0.03cm}' \cdot G\hspace{0.03cm}'+ {1}/{2}\cdot R\hspace{0.03cm}' \cdot G\hspace{0.03cm}'} \hspace{0.15cm}\underline{= 0 }\hspace{0.05cm},$$
- $$Z_{\rm W}(f = 0) = \sqrt{\frac {R\hspace{0.03cm}'}{G\hspace{0.03cm}'}} = \sqrt{\frac {100\,{\rm \Omega/km}}{{\rm 10^{-6}/(\Omega \cdot km})}}\hspace{0.15cm}\underline{= 10\, {\rm k \Omega}}\hspace{0.05cm}.$$
The DC signal attenuation becomes relevant,
- if the useful signal is to be transmitted in the baseband and has a DC component, or
- if the network termination at the participant must be supplied with power from the local exchange ("remote power supply").
(2) With $f = 10^{5} \ \rm Hz$ and the specified values, the following holds:
- $$f \cdot 2\pi L' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot 10^{-3}\,\frac{\rm \Omega \cdot s}{ {\rm km}}= 200 \,\frac{\rm \Omega }{ {\rm km}} \hspace{0.05cm},\hspace{1.05cm} f \cdot 2\pi C' = 10^5\,\frac{1}{ {\rm s}} \cdot 2 \cdot 10^{-7}\,\frac{\rm s}{ {\rm \Omega \cdot km}}= 0.02 \,\frac{\rm 1 }{ {\rm \Omega \cdot km}} \hspace{0.05cm}.$$
This results in the following for the attenuation function in "Np/km":
- $$\alpha(f = 100\,{\rm kHz}) = \sqrt{ {1}/{2}\cdot \left (100 \cdot 10^{-6} - 200 \cdot 0.02 \right)+ {1}/{2} \cdot \sqrt{(100^2 + 200^2) \cdot (10^{-12} + 0.02^2)}} $$
- $$ \Rightarrow \; \; \alpha(f = 100\,{\rm kHz}) \approx \sqrt{{1}/{2}\cdot \left (10^{-4} - 4 \right)+ {1}/{2}\cdot \sqrt{5 \cdot 10^{4} \cdot 4 \cdot 10^{-4}}} \approx \sqrt {-2 + \frac{\sqrt{20}}{ 2}} \hspace{0.15cm}\underline{\approx 0.486 \ {\rm Np/km}} \hspace{0.05cm}.$$
(3) The limit for $f → \infty$ results if one neglects the second terms in the numerator $R\hspace{0.03cm}'$ and in the denominator $G\hspace{0.08cm}'$ :
- $$\lim_{f \rightarrow \infty} \hspace{0.1cm} Z_{\rm W}(f) = \lim_{\omega \rightarrow \infty} \hspace{0.1cm} \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot \omega L'}{G' + {\rm j} \cdot \omega C\hspace{0.03cm}'}} =\sqrt{\frac {2 \pi L\hspace{0.03cm}' }{2 \pi C\hspace{0.03cm}'}}=\sqrt{\frac {2 \cdot 10^{-3}\,{\rm \Omega \cdot s} } {2 \cdot 10^{-73}\,{\rm s/\Omega} }} \hspace{0.15cm}\underline{= 100\,{\rm \Omega }}\hspace{0.05cm}.$$
- The approximation for the attenuation function is more difficult to derive. Starting from
- $$\alpha(\omega) = \sqrt{ {1}/{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ {1}/{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot C\hspace{0.03cm}\hspace{0.03cm}'^2)}}$$
- then also the following applies:
- $$2 \cdot \alpha^2(\omega) = R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' C'\cdot \left [-1 +\sqrt{(1 + \frac{R\hspace{0.03cm}'^2}{ \omega^2 \cdot L\hspace{0.03cm}'^2}) \cdot (1 + \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2})} \hspace{0.1cm} \right]$$
- $$\Rightarrow \; \; 2 \cdot \alpha^2(\omega) \approx R\hspace{0.03cm}' G\hspace{0.03cm}' + \omega^2 \cdot L' C\hspace{0.03cm}'\cdot \left [-1 +\sqrt{1 + \frac{R'^2}{ \omega^2 \cdot L'^2}+ \frac{G\hspace{0.03cm}'^2}{ \omega^2 \cdot C\hspace{0.03cm}'^2}} \hspace{0.1cm} \right].$$
- Using the approximation $\sqrt{1 + x}\approx 1+x/2$ valid for small $x$, one arrives at the intermediate result for (infinitely) large frequencies:
- $$2 \cdot \alpha^2(\omega \rightarrow \infty) = R\hspace{0.03cm}' G\hspace{0.05cm}' + \omega^2 \cdot L' C\hspace{0.05cm}'\cdot \left [ -1 +1 + {1}/{2} \cdot \left ( \frac{R\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2}+ \frac{G\hspace{0.03cm}'\hspace{0.03cm}^2}{ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2} \right) \hspace{0.1cm} \right] $$
- $$\Rightarrow \hspace{0.3cm} 2 \cdot \alpha^2(\omega \rightarrow \infty) = \frac{2 \cdot R\hspace{0.03cm}' G\hspace{0.03cm}' C\hspace{0.03cm}' L'+ R\hspace{0.03cm}'\hspace{0.03cm}^2 C\hspace{0.03cm}'\hspace{0.03cm}^2+ G\hspace{0.03cm}'\hspace{0.03cm}^2 L\hspace{0.03cm}'\hspace{0.03cm}^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' }= \frac{(R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}')^2}{2 \cdot C\hspace{0.03cm}' L\hspace{0.03cm}' }$$
- $$\Rightarrow \hspace{0.3cm} \alpha(\omega \rightarrow \infty) = {1}/{2}\cdot \frac{R\hspace{0.03cm}' C\hspace{0.03cm}' + G\hspace{0.03cm}' L\hspace{0.03cm}'}{\sqrt{ C\hspace{0.03cm}' L\hspace{0.03cm}' }}= {1}/{2}\cdot \left [R\hspace{0.03cm}' \cdot \sqrt{\frac{C\hspace{0.03cm}'}{L\hspace{0.03cm}'}}+G\hspace{0.03cm}' \cdot \sqrt{\frac{L\hspace{0.03cm}'}{C\hspace{0.03cm}'}}\right]\hspace{0.05cm}.$$
- With the numerical values inserted, we get
- $$\alpha(f \rightarrow \infty) = \alpha(\omega \rightarrow \infty) = {0.5\,{\rm Np/km}}\cdot \left [100 \cdot \sqrt{\frac{2 \cdot 10^{-7}}{2 \cdot10^{-3}}}+10^{-6} \cdot \sqrt{\frac{2 \cdot10^{-3}}{2 \cdot10^{-7}}}\right] \hspace{0.15cm}\underline{\approx 0.5 \, {\rm Np}/{\rm km}}\hspace{0.05cm}.$$
(4) For small frequencies, $\omega L\hspace{0.03cm}' \ll R\hspace{0.03cm}'$ and $ \omega C\hspace{0.03cm}' \gg G\hspace{0.03cm}'$ apply.
- Neglecting the $\omega^2$–part, one obtains:
- $$\alpha(f) = \sqrt{\frac {1}{2}\cdot \left (R\hspace{0.03cm}' G\hspace{0.03cm}' - \omega^2 \cdot L\hspace{0.03cm}' C\hspace{0.03cm}'\right)+ \frac {1}{2}\sqrt{(R\hspace{0.03cm}'\hspace{0.03cm}^2 + \omega^2 \cdot L\hspace{0.03cm}'\hspace{0.03cm}^2) \cdot (G\hspace{0.03cm}'\hspace{0.03cm}^2+ \omega^2 \cdot C\hspace{0.03cm}'\hspace{0.03cm}^2)}} \hspace{0.1cm}\bigg |_{\hspace{0.05cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}$$
- $$ \Rightarrow \hspace{0.3cm} \alpha(f) \approx \sqrt{\frac {R\hspace{0.03cm}' G\hspace{0.03cm}'}{2}+ \frac {R\hspace{0.03cm}' \cdot \omega C\hspace{0.03cm}'}{2}} \hspace{0.1cm}\bigg |_{\hspace{0.03cm}\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f} \approx \sqrt{ {1}/{2} \cdot f \cdot R\hspace{0.03cm}' \cdot 2 \pi C\hspace{0.03cm}'} \hspace{0.05cm}.$$
- Here it is considered that the first part can be neglected according to subtask (1) except for the frequency $f = 0$ .
- For the frequency $f = 1 \ \rm kHz$ we get the approximation
- $$\alpha(f = 1\,{\rm kHz}) = \sqrt{ {1}/{2} \cdot 10^{3}\,{\rm Hz} \cdot 100\,\frac{\rm \Omega }{ {\rm km}} \cdot 2 \cdot 10^{-7} \,\frac{\rm s }{ {\rm \Omega \cdot km}}} \hspace{0.15cm}\underline{= 0.1\,{\rm Np }/{ {\rm km}}} \hspace{0.05cm}.$$
- For frequency $f = 4 \ \rm kHz$ the attenuation function per unit length is twice as large:
- $$\alpha(f = 4\,{\rm kHz}) \hspace{0.15cm}\underline{ = 0.2\,{\rm Np }/{ {\rm km}}} \hspace{0.05cm}.$$
(5) The wave impedance at low frequencies is approximated by:
- $$Z_{\rm W}(f) = \sqrt{\frac {R\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi L\hspace{0.03cm}'}{G\hspace{0.03cm}' + {\rm j} \cdot f \cdot 2 \pi C\hspace{0.03cm}'}} \approx \sqrt\frac{1 }{ {\rm j}} \cdot \sqrt{\frac {R\hspace{0.03cm}' }{ f \cdot 2 \pi C\hspace{0.03cm}'}}= (1 - {\rm j})\cdot \sqrt{\frac {R\hspace{0.03cm}' }{ 2 \cdot f \cdot 2 \pi C\hspace{0.03cm}'}}\hspace{0.05cm}.$$
- With the specified line fittings we obtain:
- $${\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = \sqrt{\frac {100\,{\rm \Omega/km }}{ 2 \cdot 10^{3}\,{\rm Hz} \cdot 2 \cdot 10^{-7} \,{\rm s/(\Omega \cdot km) }}} \hspace{0.15cm}\underline{= 500\,{\rm \Omega}}\hspace{0.05cm},$$
- $$ {\rm Im}\{Z_{\rm W}(f= 1\,{\rm kHz})\} = -{\rm Re}\{Z_{\rm W}(f= 1\,{\rm kHz})\}\hspace{0.15cm}\underline{= -500\,{\rm \Omega}}\hspace{0.05cm}.$$