Difference between revisions of "Aufgaben:Exercise 3.10: Rayleigh Fading"
m (Text replacement - "root mean square" to "standard deviation") |
|||
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Further_Distributions |
}} | }} | ||
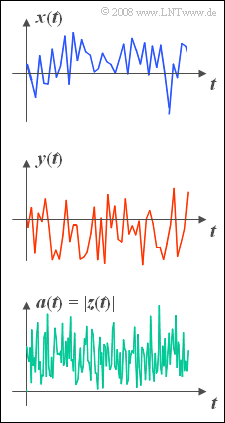
| − | [[File:P_ID177__Sto_A_3_10.png|right| | + | [[File:P_ID177__Sto_A_3_10.png|right|frame|Rayleigh distribution: real part, imaginary part, magnitude ]] |
| − | + | One often describes a band-pass transmission system in the so-called "equivalent low-pass domain". This representation leads according to the chapter "Band-pass signals" in the book [[Signal Representation]] to a complex signal: | |
| − | $$z(t)=x(t)+ {\rm j} \cdot y(t).$$ | + | :$$z(t)=x(t)+ {\rm j} \cdot y(t).$$ |
| − | + | The real part $x(t)$ denotes the "inphase component" and the imaginary part $y(t)$ the "quadrature component". | |
| − | + | In a mobile radio system where there is no line of sight between the mobile user and the base station, the radio signal thus reaches the receiver exclusively by indirect means (refraction, scattering, reflection, etc.); | |
| − | |||
| − | |||
| − | |||
| + | In this case, the following model is applicable: | ||
| + | *The real part $x(t)$ and also the imaginary part $y(t)$ are both Gaussian distributed and zero mean. | ||
| + | *$x(t)$ and $y(t)$ each have the same standard deviation $\sigma$ and are independent of each other. | ||
| + | *Internal bindings of the signals $x(t)$ and $y(t)$ due to the Doppler effect shall not be considered here. | ||
| − | + | ||
| − | $$ z(t)= a(t)\cdot {\rm e}^ | + | The complex signal $z(t)$ can also be represented by magnitude and phase: |
| − | * | + | :$$ z(t)= a(t)\cdot {\rm e}^{\rm j \phi(t)}.$$ |
| − | * | + | *Because of symmetry with respect to $x(t)$ and $y(t)$ the phase $\phi(t)$ is uniformly distributed. |
| − | * | + | *In contrast, the magnitude $a(t) = |z(t)|$ is Rayleigh distributed, which has led to the naming "Rayleigh fading". |
| + | *As a further quantity we define the instantaneous power | ||
:$$ p(t)=x^{\rm 2}(t)+y^{\rm 2}( t)=a^{\rm 2}(t).$$ | :$$ p(t)=x^{\rm 2}(t)+y^{\rm 2}( t)=a^{\rm 2}(t).$$ | ||
| − | + | The random variable $p$ is [[Theory_of_Stochastic_Signals/Exponentially_Distributed_Random_Variables#One-sided_exponential_distribution|(one-sided) exponentially distributed]]. Its PDF is for $p>0$: | |
:$$f_p(p)=\frac{1}{2\sigma^{\rm 2}}\cdot {\rm e}^{ -p/(\sigma^{\rm 2})}.$$ | :$$f_p(p)=\frac{1}{2\sigma^{\rm 2}}\cdot {\rm e}^{ -p/(\sigma^{\rm 2})}.$$ | ||
| − | + | For all negative $p$–values, of course $f_p(p)= 0$ holds, since $p$ denotes a power. | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Further_Distributions|Further Distributions]]. | ||
| + | *In particular, reference is made to the section [[Theory_of_Stochastic_Signals/Further_Distributions#Rayleigh_PDF|Rayleigh PDF]]. | ||
| + | *The standard deviation of the two Gaussian random variables $x$ and $y$ are each $\sigma = 1$. | ||
| + | *All variables are therefore to be understood as normalized. | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are always true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Small instantaneous powers are more likely than large ones. |
| − | - | + | - The phase $\phi(t) = \pi/2$ also means "imaginary part $y(t) = 0$". |
| − | + | + | + The phase $\phi(t) = -\pi/2$ also means "real part $x(t) = 0$". |
| − | { | + | {With what probability is the (normalized) instantaneous power $p(t)$ greater than $4$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(p(t) > 4)$ | + | ${\rm Pr}(p(t) > 4) \ = \ $ { 13.5 3% } $\ \%$ |
| − | { | + | {What is the probability that the magnitude $a(t)$ is greater than $2$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(a(t) > 2)$ | + | ${\rm Pr}(a(t) > 2) \ = \ $ { 13.5 3% } $\ \%$ |
| − | { | + | {Calculate, starting from $f_p(p)$ the PDF of the random variable $a$. What PDF value results for $a=1$? |
|type="{}"} | |type="{}"} | ||
| − | $f_a(a = 1)$ | + | $f_a(a = 1)\ = \ $ { 0.607 3% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Correct are <u>the first and the third proposed solutions</u>: | |
| + | *The first statement is true because of the exponential distribution for $p(t)$. | ||
| + | * A phase angle $\phi(t) = \pm \pi/2 \ (\pm 90^\circ)$ means that the real part $x(t) = 0$. | ||
| + | * For positive imaginary part ⇒ $y(t) > 0$ the phase angle $\phi(t) = +90^\circ$, for negative imaginary part the phase angle $\phi(t) = -90^\circ$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' With $\sigma = 1$ holds for the PDF of the instantaneous power: | ||
| + | :$$f_p(p)= {\rm 1}/{\rm 2}\cdot{\rm e}^{-p/\rm 2}.$$ | ||
| + | |||
| + | *The probability we are looking for is thus: | ||
| + | :$${\rm Pr}(p(t) > 4) = \int_{\rm 4}^{\infty}{1}/{2}\cdot{\rm e}^{-p/\rm 2}\,{\rm d} p={\rm e}^{\rm -2} \rm \hspace{0.15cm}\underline{=13.5\%}.$$ | ||
| + | |||
| − | |||
| − | |||
| − | + | '''(3)''' Since $p(t) =a^2(t)$ holds and moreover $a(t) < 0$ is not possible, the event $a(t) > 2$ is identical to the event $p(t) > 4$: | |
| − | |||
| − | + | *It results in the same probability ${\rm Pr}(a(t) > 2) \hspace{0.15cm}\underline{=13.5\%}$ as calculated in '''(2)''' . | |
| − | |||
| − | |||
| − | + | '''(4)''' In general: | |
| − | :$$ | + | :$$f_a(a)=\frac{f_p(p)}{|g'(p)|}\Bigg |_{\, p=h(a)}.$$ |
| − | + | *The transformation characteristic is: | |
| − | :$$\ | + | :$$g\hspace{0.05cm}'(p)=\frac{ {\rm d} a}{ {\rm d} p}=\frac{1}{2 \cdot \sqrt{p}}.$$ |
| − | + | *This is always positive. It follows for the Rayleigh PDF: | |
| + | :$$f_a(a)=\sqrt {p}\cdot {\rm e}^{ -p/\rm 2}\Big|_{ p=a^{\rm 2}}= a\cdot {\rm e}^{\, -a^{\rm 2}/\rm 2}.$$ | ||
| + | *For $a = 1$ this gives the value $f_a(a = 1)= {\rm e}^{-0.5}\hspace{0.15cm}\underline{=0.607} $. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.7 Further Distributions^]] |
Latest revision as of 12:01, 17 February 2022
One often describes a band-pass transmission system in the so-called "equivalent low-pass domain". This representation leads according to the chapter "Band-pass signals" in the book Signal Representation to a complex signal:
- $$z(t)=x(t)+ {\rm j} \cdot y(t).$$
The real part $x(t)$ denotes the "inphase component" and the imaginary part $y(t)$ the "quadrature component".
In a mobile radio system where there is no line of sight between the mobile user and the base station, the radio signal thus reaches the receiver exclusively by indirect means (refraction, scattering, reflection, etc.);
In this case, the following model is applicable:
- The real part $x(t)$ and also the imaginary part $y(t)$ are both Gaussian distributed and zero mean.
- $x(t)$ and $y(t)$ each have the same standard deviation $\sigma$ and are independent of each other.
- Internal bindings of the signals $x(t)$ and $y(t)$ due to the Doppler effect shall not be considered here.
The complex signal $z(t)$ can also be represented by magnitude and phase:
- $$ z(t)= a(t)\cdot {\rm e}^{\rm j \phi(t)}.$$
- Because of symmetry with respect to $x(t)$ and $y(t)$ the phase $\phi(t)$ is uniformly distributed.
- In contrast, the magnitude $a(t) = |z(t)|$ is Rayleigh distributed, which has led to the naming "Rayleigh fading".
- As a further quantity we define the instantaneous power
- $$ p(t)=x^{\rm 2}(t)+y^{\rm 2}( t)=a^{\rm 2}(t).$$
The random variable $p$ is (one-sided) exponentially distributed. Its PDF is for $p>0$:
- $$f_p(p)=\frac{1}{2\sigma^{\rm 2}}\cdot {\rm e}^{ -p/(\sigma^{\rm 2})}.$$
For all negative $p$–values, of course $f_p(p)= 0$ holds, since $p$ denotes a power.
Hints:
- This exercise belongs to the chapter Further Distributions.
- In particular, reference is made to the section Rayleigh PDF.
- The standard deviation of the two Gaussian random variables $x$ and $y$ are each $\sigma = 1$.
- All variables are therefore to be understood as normalized.
Questions
Solution
- The first statement is true because of the exponential distribution for $p(t)$.
- A phase angle $\phi(t) = \pm \pi/2 \ (\pm 90^\circ)$ means that the real part $x(t) = 0$.
- For positive imaginary part ⇒ $y(t) > 0$ the phase angle $\phi(t) = +90^\circ$, for negative imaginary part the phase angle $\phi(t) = -90^\circ$.
(2) With $\sigma = 1$ holds for the PDF of the instantaneous power:
- $$f_p(p)= {\rm 1}/{\rm 2}\cdot{\rm e}^{-p/\rm 2}.$$
- The probability we are looking for is thus:
- $${\rm Pr}(p(t) > 4) = \int_{\rm 4}^{\infty}{1}/{2}\cdot{\rm e}^{-p/\rm 2}\,{\rm d} p={\rm e}^{\rm -2} \rm \hspace{0.15cm}\underline{=13.5\%}.$$
(3) Since $p(t) =a^2(t)$ holds and moreover $a(t) < 0$ is not possible, the event $a(t) > 2$ is identical to the event $p(t) > 4$:
- It results in the same probability ${\rm Pr}(a(t) > 2) \hspace{0.15cm}\underline{=13.5\%}$ as calculated in (2) .
(4) In general:
- $$f_a(a)=\frac{f_p(p)}{|g'(p)|}\Bigg |_{\, p=h(a)}.$$
- The transformation characteristic is:
- $$g\hspace{0.05cm}'(p)=\frac{ {\rm d} a}{ {\rm d} p}=\frac{1}{2 \cdot \sqrt{p}}.$$
- This is always positive. It follows for the Rayleigh PDF:
- $$f_a(a)=\sqrt {p}\cdot {\rm e}^{ -p/\rm 2}\Big|_{ p=a^{\rm 2}}= a\cdot {\rm e}^{\, -a^{\rm 2}/\rm 2}.$$
- For $a = 1$ this gives the value $f_a(a = 1)= {\rm e}^{-0.5}\hspace{0.15cm}\underline{=0.607} $.