Difference between revisions of "Aufgaben:Exercise 4.11: C Program "acf1""
From LNTwww
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Auto-Correlation_Function |
}} | }} | ||
| − | [[File: | + | [[File:EN_Sto_A_4_11_neu2.png|right|frame|C program $1$ for the ACF calculation]] |
| − | + | See the C–program "acf1" for calculating the discrete ACF values $\varphi_x(k)$ with index $k = 0$, ... , $l$. The following should be noted about this: | |
| − | * | + | * The long–value passed to the program is $l = 10$. The ACF values $\varphi_x(0)$, ... , $\varphi_x(10)$ are returned to the calling program with the float field $\rm ACF\big[ \ \big]$. In lines 7 and 8 of the program given on the right, this field is pre-populated with zeros. |
| − | * | + | * The random variables $x_\nu$ to be analyzed are generated with the float function $x( \ )$, see line 4. This function is called a total of $N + l + 1 = 10011$ times $x_\nu$ (lines 9 and 18). |
| − | * | + | * In contrast to the algorithm given in the [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Numerical_ACF_determination|Theory section]] directly implemented in the program "acf2" of [[Aufgaben:Exercise_4.11Z:_C_Program_"acf2"|Task 4.11Z]], one needs here an auxiliary field ${\rm H}\big[ \ \big]$ with only $l + 1 = 11$ memory elements. |
| − | * | + | * Before starting the actual calculation algorithm (lines 11 to 21), the eleven memory cells of ${\rm H}\big[ \ \big]$ contain the random values $x_1$, ... , $x_{11}$. The outer loop with the index $z$ (marked in red) is run $N$ times. |
| + | *In the inner loop (marked white) with the index $k = 0$, ... , $l$ all memory cells of the field ${\rm ACF}\big[\hspace{0.03cm} k \hspace{0.03cm} \big]$ are increased by the contribution $x_\nu \cdot x_{\nu+k}$. | ||
| − | * | + | * Finally, in lines 22 and 23, all ACF values are divided by the number $N$ of analyzed data. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | Hint: |
| + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]]. | ||
| + | *Reference is made in particular to the page [[Theory_of_Stochastic_Signals/Auto-Correlation_Function#Numerical_ACF_determination|Numerical ACF determination]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which elements $i$ and $j$ of the auxiliary field ${\rm H}\big[ \ \big]$ are used <u>on the first loop pass</u> $(z=0)$ to calculate the ACF–value $\varphi(k=6)$ ? <br>What random values $x_\nu$ are in these memory cells? |
|type="{}"} | |type="{}"} | ||
| − | $i \ = $ | + | $i \ = \ $ { 0. } |
| − | $j \ = $ { 6 } | + | $j \ = \ $ { 6 } |
| − | { | + | {Which memory cell ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm} \big]$ will be occupied <u>after the first loop pass</u> $(z=0)$ with a new random variable $x_\nu$ ? <br> Which index $\nu$ is entered in the process? |
|type="{}"} | |type="{}"} | ||
| − | $i \ = $ { 0. } | + | $i \ = \ $ { 0. } |
| − | $\nu\ =$ { 12 } | + | $\nu\ =\ $ { 12 } |
| − | { | + | {Which memory elements ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm} \big]$ and ${\rm H}\big[\hspace{0.03cm} j \hspace{0.03cm} \big]$ are used in the loop pass $z=83$ to calculate the ACF value $\varphi(k=6)$ ? <br>What random values are in these memory cells? |
|type="{}"} | |type="{}"} | ||
| − | $i \ = $ { 6 } | + | $i \ = \ $ { 6 } |
| − | $j \ = $ { 1 } | + | $j \ = \ $ { 1 } |
| Line 51: | Line 54: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
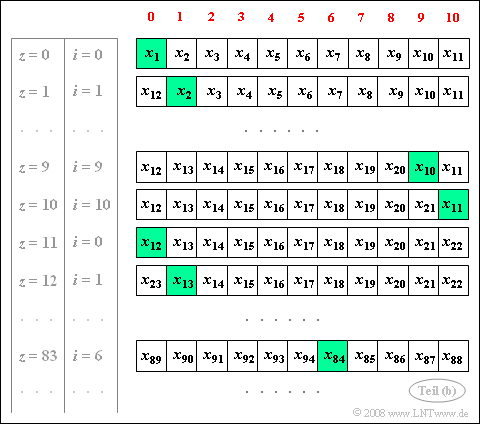
| − | '''(1)''' | + | [[File:P_ID417__Sto_A_4_11_b.png|right|frame|For the exemplary numerical ACF calculation]] |
| − | + | <br> | |
| + | '''(1)''' With $z= 0$ and $k=6$ results according to the program: $\underline{i= 0}$ and $\underline{j= 6}$. | ||
| + | *The corresponding memory contents are ${\rm H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big] = x_1$ and ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big] = x_7$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' In the field ${\rm H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big]$ the random variable $x_{12}$ is now entered: | ||
| + | :$$\text{memory cell }\underline{i= 0},\hspace{1cm}\text{sequence index }\underline{\nu= 12}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(3)''' The graph shows the allocation of the auxiliary field with the random values $x_\nu$. | |
| − | * | + | *In each case, the memory cell ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm}\big]$ is highlighted in green. The new random variable is entered into this memory location at the end of each loop (line 18). |
| − | * | + | *For $z= 83$ and $K=6$ this results in |
| − | *In | + | :$$\underline{i= 83 \hspace{-0.2cm}\mod \hspace{-0.15cm} \ 11 = 6},\hspace{1cm} \underline{j= (i+k)\hspace{-0.2cm}\mod \hspace{-0.15cm} \ 11 = 1}.$$ |
| − | * | + | *Loop pass $z= 83$: In memory cell ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$ is the random variable $x_{84}$ and in the memory cell ${\rm H}\big[\hspace{0.03cm} 1 \hspace{0.03cm}\big]$ is the random variable $x_{90}$. |
| + | *At the end of loop pass $z= 83$ in ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$: The content $x_{84}$ is replaced by $x_{95}$ . | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^4.4 Auto-Correlation Function^]] |
Latest revision as of 16:28, 28 April 2022
See the C–program "acf1" for calculating the discrete ACF values $\varphi_x(k)$ with index $k = 0$, ... , $l$. The following should be noted about this:
- The long–value passed to the program is $l = 10$. The ACF values $\varphi_x(0)$, ... , $\varphi_x(10)$ are returned to the calling program with the float field $\rm ACF\big[ \ \big]$. In lines 7 and 8 of the program given on the right, this field is pre-populated with zeros.
- The random variables $x_\nu$ to be analyzed are generated with the float function $x( \ )$, see line 4. This function is called a total of $N + l + 1 = 10011$ times $x_\nu$ (lines 9 and 18).
- In contrast to the algorithm given in the Theory section directly implemented in the program "acf2" of Task 4.11Z, one needs here an auxiliary field ${\rm H}\big[ \ \big]$ with only $l + 1 = 11$ memory elements.
- Before starting the actual calculation algorithm (lines 11 to 21), the eleven memory cells of ${\rm H}\big[ \ \big]$ contain the random values $x_1$, ... , $x_{11}$. The outer loop with the index $z$ (marked in red) is run $N$ times.
- In the inner loop (marked white) with the index $k = 0$, ... , $l$ all memory cells of the field ${\rm ACF}\big[\hspace{0.03cm} k \hspace{0.03cm} \big]$ are increased by the contribution $x_\nu \cdot x_{\nu+k}$.
- Finally, in lines 22 and 23, all ACF values are divided by the number $N$ of analyzed data.
Hint:
- This exercise belongs to the chapter Auto-Correlation Function.
- Reference is made in particular to the page Numerical ACF determination.
Questions
Solution
(1) With $z= 0$ and $k=6$ results according to the program: $\underline{i= 0}$ and $\underline{j= 6}$.
- The corresponding memory contents are ${\rm H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big] = x_1$ and ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big] = x_7$.
(2) In the field ${\rm H}\big[\hspace{0.03cm} 0 \hspace{0.03cm}\big]$ the random variable $x_{12}$ is now entered:
- $$\text{memory cell }\underline{i= 0},\hspace{1cm}\text{sequence index }\underline{\nu= 12}.$$
(3) The graph shows the allocation of the auxiliary field with the random values $x_\nu$.
- In each case, the memory cell ${\rm H}\big[\hspace{0.03cm} i \hspace{0.03cm}\big]$ is highlighted in green. The new random variable is entered into this memory location at the end of each loop (line 18).
- For $z= 83$ and $K=6$ this results in
- $$\underline{i= 83 \hspace{-0.2cm}\mod \hspace{-0.15cm} \ 11 = 6},\hspace{1cm} \underline{j= (i+k)\hspace{-0.2cm}\mod \hspace{-0.15cm} \ 11 = 1}.$$
- Loop pass $z= 83$: In memory cell ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$ is the random variable $x_{84}$ and in the memory cell ${\rm H}\big[\hspace{0.03cm} 1 \hspace{0.03cm}\big]$ is the random variable $x_{90}$.
- At the end of loop pass $z= 83$ in ${\rm H}\big[\hspace{0.03cm} 6 \hspace{0.03cm}\big]$: The content $x_{84}$ is replaced by $x_{95}$ .