Difference between revisions of "Aufgaben:Exercise 4.7Z: About the Water Filling Algorithm"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/AWGN–Kanalkapazität bei wertkontinuierlichem Eingang }} right| Wir betra…“) |
|||
| (24 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_Z_4_7.png|right|frame|Water-filling principle $(K = 4)$]] |
| − | + | We consider $K$ parallel Gaussian channels $\rm (AWGN)$ with different interference powers $\sigma_k^2$, where $1 \le k \le K$ . The graph illustrates this constellation using $K = 4$ as an example. | |
| − | $$P_1 + ... \hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K | + | |
| + | The transmission power in the individual channels is denoted by $P_k$, the sum of which must not exceed the specified value $P_X$ : | ||
| + | :$$P_1 +\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K | ||
\hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$ | \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$ | ||
| − | + | If the random variables $X_1$, ... , $X_K$ are Gaussian, then for the (total) mutual information between the input $X$ and the output $Y$ can be written: | |
| − | $$I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) | + | :$$I(X_1,\text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) |
= 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2})\hspace{0.05cm},\hspace{0.5cm} | = 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2})\hspace{0.05cm},\hspace{0.5cm} | ||
| − | {\rm | + | {\rm Result\hspace{0.15cm} in \hspace{0.15cm} \text{"bit"} } |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The maximum for this is the '''channel capacity of the total system''', where the maximization refers to the division of the total power $P_X$ among the individual channels: | |
| + | :$$C_K(P_X) = \max_{P_k\hspace{0.05cm},\hspace{0.15cm}{\rm with} \hspace{0.15cm}P_1 + ... \hspace{0.05cm}+ P_K = P_X} \hspace{-0.5cm} I(X_1, \text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) \hspace{0.05cm}.$$ | ||
| + | This maximization can be done with the "water–filling algorithm" shown in the above graph for $K = 4$. | ||
| − | === | + | In the present exercise, this algorithm is to be applied, assuming the following: |
| + | * Two parallel Gaussian channels ⇒ $K = 2$, | ||
| + | * normalized noise powers $\sigma_1^2 = 1$ and $\sigma_2^2 = 4$, | ||
| + | * normalized transmission powers $P_X = 10$ and $P_X = 3$ respectively. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN channel capacity with continuous value input]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Parallel_Gaussian_channels|Parallel Gaussian Channels]]. | ||
| + | *Since the results are to be given in "bit", the logarithm to base $2$ is used in the equations: $\log_2$. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which power allocation strategies are useful? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - A very noisy channel $k$ $($with large noise power $\sigma_k^2)$ should be allocated a large effective power $P_k$. |
| − | + | + | + A very noisy channel $k$ $($with large noise power $\sigma_k^2)$ should be assigned only a small useful power $P_k$. |
| − | + | + | + For $K$ equally good channels ⇒ $\sigma_1^2 = \text{...} = \sigma_K^2 = \sigma_N^2$ the power $P_k$ should be evenly distributed. |
| − | { | + | {What is the mutual information obtained by distributing the transmission power $P_X = 10$ equally to both channels $(P_1= P_2 = 5)$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X_1, X_2; Y_1, Y_2) \ = \ $ { 1.877 3% } $\ \rm bit$ |
| − | { | + | {Let $P_X = P_1 + P_2 = 10$ be further valid. Which optimal power distribution results according to the "water–filling algorithm"? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $P_1 \ = \ $ { 6.5 3% } |
| − | $ | + | $P_2 \ = \ $ { 3.5 3% } |
| − | { | + | {What is the channel capacity for $\underline{K = 2}$ and $\underline{P_X = 10}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $C \ = \ $ { 1.907 3% } $\ \rm bit$ |
| + | |||
| + | {What mutual information results if the transmit power $P_X = 3$ is distributed equally to both channels $(P_1= P_2 = 1.5)$? | ||
| + | |type="{}"} | ||
| + | $I(X_1, X_2; Y_1, Y_2) \ = \ $ { 0.891 3% }$\ \rm bit$ | ||
| − | { | + | {What is the channel capacity for $\underline{K = 2}$ and $\underline{P_X = 3}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $C \ = \ $ { 1 3% } $\ \rm bit$ |
| − | $ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>Proposed solutions 2 and 3</u> are correct: |
| − | '''2 | + | *According to the explanations in the theory section "Water–Filling" ⇒ <u>Proposal 2</u> is to be applied when unequal conditions exist. |
| − | '''3 | + | * However, <u>solution proposal 3</u> is also correct: If the channels are equally good, there is nothing to prevent all $K$ channels from being filled with the same power ⇒ $P_1 = P_2 =$ ... $= P_K = P_X/K$. |
| − | '''4.''' | + | |
| − | '''5.''' | + | |
| − | ''' | + | |
| − | ''' | + | '''(2)''' For the mutual information, with equal power distribution, the following applies: |
| + | :$$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{1} \right ) | ||
| + | +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{4} \right )=1.292\,{\rm bit}+ 0.585\,{\rm bit} | ||
| + | \hspace{0.15cm}\underline{= 1.877\,{\rm bit}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | [[File:EN_Inf_Z_4_7b.png|right|frame|Best possible distribution of transmit power $P_X = 10$]] | ||
| + | '''(3)''' According to the adjacent sketch, the following must apply: | ||
| + | :$$P_2 = P_1 - (\sigma_2^2 - \sigma_1^2) = P_1 -3\hspace{0.3cm}\text{wobei }\hspace{0.3cm}P_1 + P_2 = P_X = 10$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} | ||
| + | P_1 + (P_1 -3) = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | 2 \cdot P_1 = 13 \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} | ||
| + | \underline{P_1 = 6.5}\hspace{0.05cm}, | ||
| + | \hspace{0.3cm}\underline{P_2 = 3.5}\hspace{0.05cm}.$$ | ||
| + | For the "water level height" here holds: | ||
| + | :$$H= P_1 + \sigma_1^2= P_2 + \sigma_2^2 = 7.5 = 6.5+1 = 3.5+4.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' The channel capacity indicates the maximum mutual information. The maximum is already fixed by the best possible power sharing according to subtask '''(3)'''. For $P_X = 10$ holds: | ||
| + | :$$C={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{6.5}{1} \right ) | ||
| + | +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3.5}{4} \right )$$ | ||
| + | :$$\Rightarrow\hspace{0.3cm} C=1.453\,{\rm bit}+ 0.453\,{\rm bit} | ||
| + | \hspace{0.15cm}\underline{= 1.906\,{\rm bit}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' For $P_X = 3$, with the same power splitting $(P_1 = P_2 =1.5)$, we obtain: | ||
| + | :$$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{1} \right ) | ||
| + | +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{4} \right ) | ||
| + | \hspace{0.15cm}\underline{= 0.891\,{\rm bit}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | [[File:EN_Inf_Z_4_7e.png|right|frame|Best possible distribution of the transmit power $P_X = 3$]] | ||
| + | '''(6)''' According to the water–filling algorithm, the total transmission power $P_X = 3$ is now fully allocated to the first channel: | ||
| + | :$${P_1 = 3}\hspace{0.05cm}, | ||
| + | \hspace{0.3cm}{P_2 = 0}\hspace{0.05cm}.$$ | ||
| + | |||
| + | *So here for the "water level height": | ||
| + | :$$H= 4= P_1 + \sigma_1^2= P_2 + \sigma_2^2= 3+1=0+4.$$ | ||
| + | |||
| + | *This gives for the channel capacity: | ||
| + | :$$C ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3}{1} \right ) | ||
| + | +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{0}{4} \right )=1\,{\rm bit}+ 0\,{\rm bit} | ||
| + | \hspace{0.15cm}\underline{= 1\,{\rm bit}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Further notes: | ||
| + | *While for $P_X = 10$ the difference between even and best power splitting was only $0.03$ bit, for $P_X = 3$ the difference is larger: $0.109$ bit. | ||
| + | *For even larger $P_X > 10$ , the difference between even and best power splitting becomes even smaller. | ||
| + | |||
| + | |||
| + | For example, for $P_X = 100$ the difference is only $0.001$ bit as the following calculation shows: | ||
| + | *For $P_1 = P_2 = 50$ one obtains: | ||
| + | :$$I = I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{1} \right ) | ||
| + | +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{4} \right )= 2.836\,{\rm bit}+ 1.877\,{\rm bit} | ||
| + | \hspace{0.15cm}\underline{= 4.713\,{\rm bit}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *In contrast, the best possible split gives ⇒ $P_1 = 51.5, \ P_2 = 48.5$: | ||
| + | :$$C = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{51.5}{1} \right ) | ||
| + | +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{48.5}{4} \right )= 2.857\,{\rm bit}+ 1.857\,{\rm bit} | ||
| + | \hspace{0.15cm}\underline{= 4.714\,{\rm bit}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.2 AWGN and Value-Continuous Input^]] |
Latest revision as of 14:10, 7 October 2021
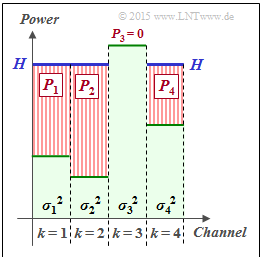
We consider $K$ parallel Gaussian channels $\rm (AWGN)$ with different interference powers $\sigma_k^2$, where $1 \le k \le K$ . The graph illustrates this constellation using $K = 4$ as an example.
The transmission power in the individual channels is denoted by $P_k$, the sum of which must not exceed the specified value $P_X$ :
- $$P_1 +\text{...}\hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$
If the random variables $X_1$, ... , $X_K$ are Gaussian, then for the (total) mutual information between the input $X$ and the output $Y$ can be written:
- $$I(X_1,\text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) = 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2})\hspace{0.05cm},\hspace{0.5cm} {\rm Result\hspace{0.15cm} in \hspace{0.15cm} \text{"bit"} } \hspace{0.05cm}.$$
The maximum for this is the channel capacity of the total system, where the maximization refers to the division of the total power $P_X$ among the individual channels:
- $$C_K(P_X) = \max_{P_k\hspace{0.05cm},\hspace{0.15cm}{\rm with} \hspace{0.15cm}P_1 + ... \hspace{0.05cm}+ P_K = P_X} \hspace{-0.5cm} I(X_1, \text{...} \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, \text{...}\hspace{0.05cm}, Y_K) \hspace{0.05cm}.$$
This maximization can be done with the "water–filling algorithm" shown in the above graph for $K = 4$.
In the present exercise, this algorithm is to be applied, assuming the following:
- Two parallel Gaussian channels ⇒ $K = 2$,
- normalized noise powers $\sigma_1^2 = 1$ and $\sigma_2^2 = 4$,
- normalized transmission powers $P_X = 10$ and $P_X = 3$ respectively.
Hints:
- The exercise belongs to the chapter AWGN channel capacity with continuous value input.
- Reference is made in particular to the page Parallel Gaussian Channels.
- Since the results are to be given in "bit", the logarithm to base $2$ is used in the equations: $\log_2$.
Questions
Solution
- According to the explanations in the theory section "Water–Filling" ⇒ Proposal 2 is to be applied when unequal conditions exist.
- However, solution proposal 3 is also correct: If the channels are equally good, there is nothing to prevent all $K$ channels from being filled with the same power ⇒ $P_1 = P_2 =$ ... $= P_K = P_X/K$.
(2) For the mutual information, with equal power distribution, the following applies:
- $$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{5}{4} \right )=1.292\,{\rm bit}+ 0.585\,{\rm bit} \hspace{0.15cm}\underline{= 1.877\,{\rm bit}} \hspace{0.05cm}.$$
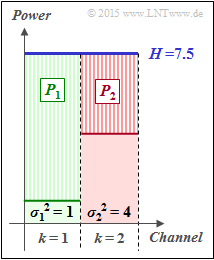
(3) According to the adjacent sketch, the following must apply:
- $$P_2 = P_1 - (\sigma_2^2 - \sigma_1^2) = P_1 -3\hspace{0.3cm}\text{wobei }\hspace{0.3cm}P_1 + P_2 = P_X = 10$$
- $$\Rightarrow \hspace{0.3cm} P_1 + (P_1 -3) = 10\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2 \cdot P_1 = 13 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{P_1 = 6.5}\hspace{0.05cm}, \hspace{0.3cm}\underline{P_2 = 3.5}\hspace{0.05cm}.$$
For the "water level height" here holds:
- $$H= P_1 + \sigma_1^2= P_2 + \sigma_2^2 = 7.5 = 6.5+1 = 3.5+4.$$
(4) The channel capacity indicates the maximum mutual information. The maximum is already fixed by the best possible power sharing according to subtask (3). For $P_X = 10$ holds:
- $$C={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{6.5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3.5}{4} \right )$$
- $$\Rightarrow\hspace{0.3cm} C=1.453\,{\rm bit}+ 0.453\,{\rm bit} \hspace{0.15cm}\underline{= 1.906\,{\rm bit}} \hspace{0.05cm}.$$
(5) For $P_X = 3$, with the same power splitting $(P_1 = P_2 =1.5)$, we obtain:
- $$I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{1.5}{4} \right ) \hspace{0.15cm}\underline{= 0.891\,{\rm bit}} \hspace{0.05cm}.$$
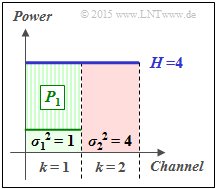
(6) According to the water–filling algorithm, the total transmission power $P_X = 3$ is now fully allocated to the first channel:
- $${P_1 = 3}\hspace{0.05cm}, \hspace{0.3cm}{P_2 = 0}\hspace{0.05cm}.$$
- So here for the "water level height":
- $$H= 4= P_1 + \sigma_1^2= P_2 + \sigma_2^2= 3+1=0+4.$$
- This gives for the channel capacity:
- $$C ={1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{3}{1} \right ) +{1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{0}{4} \right )=1\,{\rm bit}+ 0\,{\rm bit} \hspace{0.15cm}\underline{= 1\,{\rm bit}} \hspace{0.05cm}.$$
Further notes:
- While for $P_X = 10$ the difference between even and best power splitting was only $0.03$ bit, for $P_X = 3$ the difference is larger: $0.109$ bit.
- For even larger $P_X > 10$ , the difference between even and best power splitting becomes even smaller.
For example, for $P_X = 100$ the difference is only $0.001$ bit as the following calculation shows:
- For $P_1 = P_2 = 50$ one obtains:
- $$I = I(X_1, X_2\hspace{0.05cm};\hspace{0.05cm}Y_1, Y_2) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{1} \right ) +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{50}{4} \right )= 2.836\,{\rm bit}+ 1.877\,{\rm bit} \hspace{0.15cm}\underline{= 4.713\,{\rm bit}} \hspace{0.05cm}.$$
- In contrast, the best possible split gives ⇒ $P_1 = 51.5, \ P_2 = 48.5$:
- $$C = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{51.5}{1} \right ) +{1}/{2}\cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{48.5}{4} \right )= 2.857\,{\rm bit}+ 1.857\,{\rm bit} \hspace{0.15cm}\underline{= 4.714\,{\rm bit}} \hspace{0.05cm}.$$