Difference between revisions of "Aufgaben:Exercise 5.2Z: Two-Way Channel"
| (13 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Stochastic_System_Theory |
}} | }} | ||
| − | [[File:P_ID517__Sto_Z_5_2.png|right| | + | [[File:P_ID517__Sto_Z_5_2.png|right|frame|Two–way channel impulse responses $h(t)$, $h(t) * h( { - t} )$]] |
| − | + | From a transmission system it is known that following relationship exists between the input signal $x(t)$ and the output signal $y(t)$ : | |
:$$y(t) = x( {t - \tau _1 } ) + \alpha \cdot x( {t - \tau _2 } ).$$ | :$$y(t) = x( {t - \tau _1 } ) + \alpha \cdot x( {t - \tau _2 } ).$$ | ||
| − | + | The corresponding impulse response $h(t)$ is sketched above. | |
| + | In the sketch below, the function | ||
| + | :$$h(t) * h( { - t} )\hspace{0.25cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.25cm}\left| {H(f)} \right|^2$$ | ||
| − | + | is shown, where the parameters $C_0$, $C_3$ and $\tau_3$ depend on $\alpha$, $\tau_1$ and $\tau_2$ ⇒ see subtask '''(4)'''. | |
| − | |||
| − | + | Let the input signal $x(t)$ be band-limited white noise | |
| + | *with power density $N_0 = 10^{-6} \hspace{0.08cm} \rm W/Hz$ | ||
| + | *and bandwidth $B = 10 \hspace{0.08cm} \rm kHz$, | ||
| − | |||
| + | from which the power $P_x = 10 \hspace{0.08cm} \rm mW$ can be calculated. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | Notes: |
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Stochastic_System_Theory| Stochastic System Theory]]. | ||
| + | *Use always the value $\alpha = 0.5$ for numerical calculations. | ||
| + | *For the subtasks '''(1)''' and '''(2)''', let $\tau_1 = 0$ and $\tau_2 = 4\hspace{0.08cm}\rm ms$ be valid. | ||
| + | *For later tasks, assume $\tau_1 = 1\hspace{0.08cm}\rm ms$ and $\tau_2 = 5\hspace{0.08cm}\rm ms$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the frequency response $H(f)$ for $\tau_1 = 0$ and $\tau_2 = 4\hspace{0.08cm}\rm ms$. Show that $H(f)$ is a periodic function with $f_0$. What is the value of $f_0$? |
|type="{}"} | |type="{}"} | ||
| − | $f_0 \ =$ { 0.25 3% } $\ \rm kHz$ | + | $f_0 \ = \ $ { 0.25 3% } $\ \rm kHz$ |
| − | { | + | {What is the size of $|H(f)|^2$ with $\tau_1 = 0$, $\tau_2 = 4\hspace{0.08cm}\rm ms$ and $\alpha = 0.5$? Enter the value at $f = 0$. |
|type="{}"} | |type="{}"} | ||
| − | $|H(f = 0)|^2 \ =$ { 2.25 3% } | + | $|H(f = 0)|^2 \ = \ $ { 2.25 3% } |
| − | { | + | {How does $|H(f)|^2$ change with $\tau_1 = 1\hspace{0.08cm}\rm ms$ and $\tau_2 = 5\hspace{0.08cm}\rm ms$? Let the attenuation constant still be $\alpha = 0.5$. Enter the value at $f = 0$. |
|type="{}"} | |type="{}"} | ||
| − | $|H(f = 0)|^2 \ =$ { 2.25 } | + | $|H(f = 0)|^2 \ = \ $ { 2.25 } |
| − | { | + | {Let $\alpha = 0.5$, $\tau_1 = 1\hspace{0.08cm}\rm ms$ and $\tau_2 = 5\hspace{0.08cm}\rm ms$ still hold. Which values result for the function parameters of $h(t) \star h(-t)$ according to the diagram? |
|type="{}"} | |type="{}"} | ||
| − | $C_0 \ =${ 1.25 3% } | + | $C_0 \ = \ ${ 1.25 3% } |
| − | $C_3 \ =$ { 0.5 3% } | + | $C_3 \ = \ $ { 0.5 3% } |
| − | $\tau_3 \ =$ { 4 3% } $\ \rm ms$ | + | $\tau_3 \ = \ $ { 4 3% } $\ \rm ms$ |
| − | { | + | {What is the power of the output signal $y(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $P_y \ =$ { 12.5 3% } $\ \rm mW$ | + | $P_y \ = \ $ { 12.5 3% } $\ \rm mW$ |
| Line 60: | Line 66: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' $H(f)$ | + | '''(1)''' $H(f)$ is the Fourier transform to $h(t)$. |
| + | *Using the shifting theorem, this is with $\tau_1 = 0$: | ||
:$$H(f) = 1 + \alpha \cdot {\rm{e}}^{ - {\rm{j2\pi }}f\tau _2 } = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$ | :$$H(f) = 1 + \alpha \cdot {\rm{e}}^{ - {\rm{j2\pi }}f\tau _2 } = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$ | ||
| − | + | *If $H(f)$ is periodic with $f_0$, then for all integer values of $i$ must hold: | |
| + | :$$H( {f + i \cdot f_0 } ) = H( f ).$$ | ||
| + | *With $f_0 = 1/\tau_2\hspace{0.15cm} \underline{= 0.25 \hspace{0.05cm}\rm kHz}$ this condition is satisfied. | ||
:$$H( {f + i \cdot f_0 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$ | :$$H( {f + i \cdot f_0 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$ | ||
| − | '''(2)''' | + | |
| + | '''(2)''' The magnitude square is the sum of squared real part and squared imaginary part: | ||
:$$\left| {H( f )} \right|^2 = \left( {1 + \alpha \cdot \cos ( A )} \right)^2 + \left( {\alpha \cdot \sin ( A )} \right)^2 .$$ | :$$\left| {H( f )} \right|^2 = \left( {1 + \alpha \cdot \cos ( A )} \right)^2 + \left( {\alpha \cdot \sin ( A )} \right)^2 .$$ | ||
| − | + | *Here the angle argument is abbreviated as $A = 2\pi f \tau$. After multiplying, we get because of $\cos^2(A) + \sin^2(A) = 1$: | |
:$$\left| {H(f)} \right|^2 = 1 + \alpha ^2 + 2\alpha \cdot \cos ( A ).$$ | :$$\left| {H(f)} \right|^2 = 1 + \alpha ^2 + 2\alpha \cdot \cos ( A ).$$ | ||
| − | + | *At the frequency $f = 0$ $($and thus $A = 0)$, the result with $\alpha = 0.5$ is: | |
:$$\left| {H( {f = 0} )} \right|^2 = \left( {1 + \alpha } \right)^2 = 1.5^2\hspace{0.15cm} \underline{ = 2.25}.$$ | :$$\left| {H( {f = 0} )} \right|^2 = \left( {1 + \alpha } \right)^2 = 1.5^2\hspace{0.15cm} \underline{ = 2.25}.$$ | ||
| − | |||
| − | |||
| − | + | '''(3)''' Now the transmission system can be composed of two subsystems (see diagram): | |
| + | [[File:P_ID551__Sto_Z_5_2_c.png|frame|Splitting the impulse response into two subsystems]] | ||
| + | |||
| + | *The transfer function $H_1(f)$ is calculated as in subtask '''(2)'''. | ||
| + | *For $H_2(f)$ it holds with $\tau_1 = 1\hspace{0.05cm}\rm ms$: | ||
:$$H_2 (f) = {\rm{e}}^{ - {\rm{j2\pi }}f\tau _1 } \quad \Rightarrow \quad \left| {H_2 (f)} \right| = 1\quad \Rightarrow \quad \left| {H_2 (f)} \right|^2 = 1.$$ | :$$H_2 (f) = {\rm{e}}^{ - {\rm{j2\pi }}f\tau _1 } \quad \Rightarrow \quad \left| {H_2 (f)} \right| = 1\quad \Rightarrow \quad \left| {H_2 (f)} \right|^2 = 1.$$ | ||
| − | + | *This means: Due to the additional delay time, $\left| {H(f)} \right|^2$ is not changed compared to subtask '''(2)'''. | |
| + | * At the frequency $f = 0$: $\left| {H(f = 0)} \right|^2\hspace{0.15cm} \underline{ = 2.25}$ is still valid. | ||
| + | |||
| + | |||
| − | '''(4)''' | + | '''(4)''' By comparing the drawn function $h(t) \star h(-t)$ with the result of subtask '''(2)''': |
:$$C_0 = 1 + \alpha ^2 \hspace{0.15cm} \underline{= 1.25}, | :$$C_0 = 1 + \alpha ^2 \hspace{0.15cm} \underline{= 1.25}, | ||
\hspace{0.5cm}C_3 = \alpha \hspace{0.15cm} \underline{= 0.5}, | \hspace{0.5cm}C_3 = \alpha \hspace{0.15cm} \underline{= 0.5}, | ||
\hspace{0.5cm}\tau _3 = \tau _2 - \tau _1 \hspace{0.15cm} \underline{= 4\;{\rm{ms}}}.$$ | \hspace{0.5cm}\tau _3 = \tau _2 - \tau _1 \hspace{0.15cm} \underline{= 4\;{\rm{ms}}}.$$ | ||
| − | '''(5)''' | + | |
| + | '''(5)''' The power-spectral density of the output signal $y(t)$ is limited to the range of $\pm B$ and results in | ||
:$${\it \Phi}_y(f) = {N_0}/{2} \cdot |H(f)|^2 = N_0/{2} \cdot {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}.$$ | :$${\it \Phi}_y(f) = {N_0}/{2} \cdot |H(f)|^2 = N_0/{2} \cdot {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}.$$ | ||
| − | + | *Taking advantage of symmetry properties, we thus obtain for the power: | |
:$$P_y = N_0 \cdot \int_0^B {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}\hspace{0.1cm} {\rm{d}}f.$$ | :$$P_y = N_0 \cdot \int_0^B {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}\hspace{0.1cm} {\rm{d}}f.$$ | ||
| − | + | *$B = 10 \hspace{0.08cm} \rm kHz$ is an integer multiple of the frequency period $f_0 = 1/\tau_2= 250 \hspace{0.08cm}\rm Hz$ $($cf. solution to subtask '''1'''$)$. Therefore, the cosine function does not contribute to the integral, and we obtain: | |
:$$P_y = N_0 \cdot B \cdot \left( {1 + \alpha ^2 } \right) = 1.25 \cdot P_x \hspace{0.15cm} \underline{ = 12.5\;{\rm{mW}}}.$$ | :$$P_y = N_0 \cdot B \cdot \left( {1 + \alpha ^2 } \right) = 1.25 \cdot P_x \hspace{0.15cm} \underline{ = 12.5\;{\rm{mW}}}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 102: | Line 118: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^5.1 Stochastic Systems Theory^]] |
Latest revision as of 16:51, 10 February 2022
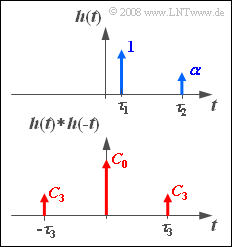
From a transmission system it is known that following relationship exists between the input signal $x(t)$ and the output signal $y(t)$ :
- $$y(t) = x( {t - \tau _1 } ) + \alpha \cdot x( {t - \tau _2 } ).$$
The corresponding impulse response $h(t)$ is sketched above.
In the sketch below, the function
- $$h(t) * h( { - t} )\hspace{0.25cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.25cm}\left| {H(f)} \right|^2$$
is shown, where the parameters $C_0$, $C_3$ and $\tau_3$ depend on $\alpha$, $\tau_1$ and $\tau_2$ ⇒ see subtask (4).
Let the input signal $x(t)$ be band-limited white noise
- with power density $N_0 = 10^{-6} \hspace{0.08cm} \rm W/Hz$
- and bandwidth $B = 10 \hspace{0.08cm} \rm kHz$,
from which the power $P_x = 10 \hspace{0.08cm} \rm mW$ can be calculated.
Notes:
- The exercise belongs to the chapter Stochastic System Theory.
- Use always the value $\alpha = 0.5$ for numerical calculations.
- For the subtasks (1) and (2), let $\tau_1 = 0$ and $\tau_2 = 4\hspace{0.08cm}\rm ms$ be valid.
- For later tasks, assume $\tau_1 = 1\hspace{0.08cm}\rm ms$ and $\tau_2 = 5\hspace{0.08cm}\rm ms$.
Questions
Solution
- Using the shifting theorem, this is with $\tau_1 = 0$:
- $$H(f) = 1 + \alpha \cdot {\rm{e}}^{ - {\rm{j2\pi }}f\tau _2 } = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$
- If $H(f)$ is periodic with $f_0$, then for all integer values of $i$ must hold:
- $$H( {f + i \cdot f_0 } ) = H( f ).$$
- With $f_0 = 1/\tau_2\hspace{0.15cm} \underline{= 0.25 \hspace{0.05cm}\rm kHz}$ this condition is satisfied.
- $$H( {f + i \cdot f_0 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$
(2) The magnitude square is the sum of squared real part and squared imaginary part:
- $$\left| {H( f )} \right|^2 = \left( {1 + \alpha \cdot \cos ( A )} \right)^2 + \left( {\alpha \cdot \sin ( A )} \right)^2 .$$
- Here the angle argument is abbreviated as $A = 2\pi f \tau$. After multiplying, we get because of $\cos^2(A) + \sin^2(A) = 1$:
- $$\left| {H(f)} \right|^2 = 1 + \alpha ^2 + 2\alpha \cdot \cos ( A ).$$
- At the frequency $f = 0$ $($and thus $A = 0)$, the result with $\alpha = 0.5$ is:
- $$\left| {H( {f = 0} )} \right|^2 = \left( {1 + \alpha } \right)^2 = 1.5^2\hspace{0.15cm} \underline{ = 2.25}.$$
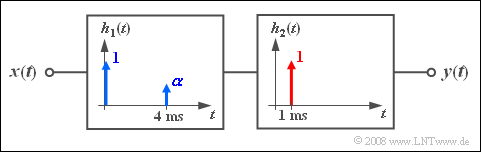
(3) Now the transmission system can be composed of two subsystems (see diagram):
- The transfer function $H_1(f)$ is calculated as in subtask (2).
- For $H_2(f)$ it holds with $\tau_1 = 1\hspace{0.05cm}\rm ms$:
- $$H_2 (f) = {\rm{e}}^{ - {\rm{j2\pi }}f\tau _1 } \quad \Rightarrow \quad \left| {H_2 (f)} \right| = 1\quad \Rightarrow \quad \left| {H_2 (f)} \right|^2 = 1.$$
- This means: Due to the additional delay time, $\left| {H(f)} \right|^2$ is not changed compared to subtask (2).
- At the frequency $f = 0$: $\left| {H(f = 0)} \right|^2\hspace{0.15cm} \underline{ = 2.25}$ is still valid.
(4) By comparing the drawn function $h(t) \star h(-t)$ with the result of subtask (2):
- $$C_0 = 1 + \alpha ^2 \hspace{0.15cm} \underline{= 1.25}, \hspace{0.5cm}C_3 = \alpha \hspace{0.15cm} \underline{= 0.5}, \hspace{0.5cm}\tau _3 = \tau _2 - \tau _1 \hspace{0.15cm} \underline{= 4\;{\rm{ms}}}.$$
(5) The power-spectral density of the output signal $y(t)$ is limited to the range of $\pm B$ and results in
- $${\it \Phi}_y(f) = {N_0}/{2} \cdot |H(f)|^2 = N_0/{2} \cdot {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}.$$
- Taking advantage of symmetry properties, we thus obtain for the power:
- $$P_y = N_0 \cdot \int_0^B {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}\hspace{0.1cm} {\rm{d}}f.$$
- $B = 10 \hspace{0.08cm} \rm kHz$ is an integer multiple of the frequency period $f_0 = 1/\tau_2= 250 \hspace{0.08cm}\rm Hz$ $($cf. solution to subtask 1$)$. Therefore, the cosine function does not contribute to the integral, and we obtain:
- $$P_y = N_0 \cdot B \cdot \left( {1 + \alpha ^2 } \right) = 1.25 \cdot P_x \hspace{0.15cm} \underline{ = 12.5\;{\rm{mW}}}.$$