Difference between revisions of "Aufgaben:Exercise 4.5: Mutual Information from 2D-PDF"
m (Text replacement - "value-continuous" to "continuous") |
|||
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input |
}} | }} | ||
| − | [[File:P_ID2886__Inf_A_4_5_neu.png|right|]] | + | [[File:P_ID2886__Inf_A_4_5_neu.png|right|frame|Given joint PDF]] |
| − | + | Given here are the three different two-dimensional regions $f_{XY}(x, y)$, which in the task are identified by their fill colors with | |
| − | + | * red joint PDF, | |
| − | + | * blue joint PDF, | |
| − | + | * green joint PDF, | |
| − | |||
| − | + | respectively. Within each of the regions shown, let $f_{XY}(x, y) = C = \rm const.$ | |
| − | $ | ||
| − | + | For example, the mutual information between the continuous random variables $X$ and $Y$ can be calculated as follows: | |
| − | $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x | + | :$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$ |
| + | |||
| + | For the differential entropies used here, the following equations apply: | ||
| + | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | $$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y | + | :$$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | $$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} | + | :$$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} |
| − | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} [ f_{XY}(x, y) ] | + | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[ f_{XY}(x, y) \big] |
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| − | + | *For the two marginal probability density functions, the following holds: | |
| − | $$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) | + | :$$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) |
| − | \hspace{0.15cm}{\rm d}y\hspace{0.05cm}, | + | \hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$ |
| − | f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) | + | :$$f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) |
\hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$ | ||
| − | + | ||
| − | :* | + | |
| − | $$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$ | + | |
| − | :* | + | |
| − | $$h(Y) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}]\hspace{0.05cm}.$$ | + | |
| − | + | ||
| − | === | + | |
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input#Mutual_information_between_continuous_random_variables|Mutual information with continuous input]]. | ||
| + | |||
| + | *Let the following differential entropies also be given: | ||
| + | :* If $X$ is triangularly distributed between $x_{\rm min}$ and $x_{\rm max}$, then: | ||
| + | ::$$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$ | ||
| + | :* If $Y$ is equally distributed between $y_{\rm min}$ and $y_{\rm max}$, then holds: | ||
| + | ::$$h(Y) = {\rm log} \hspace{0.1cm} \big [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}\big ]\hspace{0.05cm}.$$ | ||
| + | *All results should be expressed in "bit". This is achieved with $\log$ ⇒ $\log_2$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the mutual information of <u>the red joint PDF</u>? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X; Y) \ = \ $ { 0. } $\ \rm bit$ |
| − | { | + | {What is the mutual information of <u>the blue joint PDF</u>? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X; Y) \ = \ $ { 0.721 3% } $\ \rm bit$ |
| − | { | + | {What is the mutual information of <u>the green joint PDF</u>? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X; Y) \ = \ $ { 0.721 3% } $\ \rm bit$ |
| − | { | + | {What conditions must the random variables $X$ and $Y$ satisfy simultaneously for $I(X;Y) = 1/2 \cdot \log (\rm e)$ to hold in general? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The two-dimensional PDF $f_{XY}(x, y)$ results in a parallelogram. |
| − | + | + | + One of the random variables $(X$ or $Y)$ is uniformly distributed. |
| − | + | + | + The other random variable $(Y$ or $X)$ is triangularly distributed. |
| Line 60: | Line 76: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID2887__Inf_A_4_5a.png|right| | + | [[File:P_ID2887__Inf_A_4_5a.png|right|frame|"Red" probability density functions; <br>'''!''' Note: Ordinate of $f_{Y}(y)$ is directed to the left '''!''']] |
| − | < | + | '''(1)''' For the rectangular two-dimensional PDF $f_{XY}(x, y)$ there are no statistical dependences between $X$ and $Y$ ⇒ $\underline{I(X;Y) = 0}$. |
| − | |||
| − | |||
| − | $$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$ | + | Formally, this result can be proved with the following equation: |
| − | + | :$$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$ | |
| − | $$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | + | *The red area of the two-dimensional PDF $f_{XY}(x, y)$ is $F = 4$. |
| + | *Since $f_{XY}(x, y)$ is constant in this area and the volume under $f_{XY}(x, y)$ must be equal to $1$, the height is $C = 1/F = 1/4$. | ||
| + | *From this follows for the differential joint entropy in "bit": | ||
| + | :$$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | ||
\hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] | ||
| − | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\\ | + | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$ |
| − | = \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | + | :$$\Rightarrow \hspace{0.3cm} h(XY) \ = \ \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} |
\hspace{-0.6cm} f_{XY}(x, y) | \hspace{-0.6cm} f_{XY}(x, y) | ||
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$ | ||
| − | + | *It is considered that the double integral is equal to $1$ . The pseudo-unit "bit" corresponds to the "binary logarithm" ⇒ "log<sub>2</sub>". | |
| − | + | ||
| − | $$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$ | + | |
| − | :* | + | Furthermore: |
| − | $$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} | + | |
| + | * The marginal probability density functions $f_{X}(x)$ and $f_{Y}(y)$ are rectangular ⇒ uniform distribution between $0$ and $2$: | ||
| + | :$$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$ | ||
| + | [[File:P_ID2888__Inf_A_4_5b_neu.png|right|frame|"Blue" | ||
| + | probability density functions]] | ||
| + | |||
| + | * Substituting these results into the above equation, we obtain: | ||
| + | :$$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | + | ||
| − | $$h(X) = {\rm log}_2 \hspace{0.1cm} [\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}] | + | |
| + | '''(2)''' Also for this parallelogram we get $F = 4, \ C = 1/4$ as well as $h(XY) = 2$ bit. | ||
| + | * Here, as in subtask '''(1)''' , the variable $Y$ is uniformly distributed between $0$ and $2$ ⇒ $h(Y) = 1$ bit. | ||
| + | |||
| + | *In contrast, $X$ is triangularly distributed between $0$ and $4$ $($with maximum at $2)$. | ||
| + | *This results in the same differential entropy $h(Y)$ as for a symmetric triangular distribution in the range between $±2$ (see specification sheet): | ||
| + | :$$h(X) = {\rm log}_2 \hspace{0.1cm} \big[\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}\big ] | ||
= 1.721 \,{\rm bit}$$ | = 1.721 \,{\rm bit}$$ | ||
| − | $$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} | + | :$$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | [[File:P_ID2889__Inf_A_4_5c_neu.png|right|]] | + | <br clear=all> |
| − | + | [[File:P_ID2889__Inf_A_4_5c_neu.png|right|frame|"„Green" probability density functions]] | |
| − | $$F = A \cdot B \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \frac{1}{A \cdot B} | + | '''(3)''' The following properties are obtained for the green conditions: |
| − | \hspace{0.05cm} | + | :$$F = A \cdot B \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \frac{1}{A \cdot B} |
| − | + | \hspace{0.05cm}\hspace{0.3cm} | |
| + | \Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *The random variable $Y$ is now uniformly distributed between $0$ and $A$ and the random variable $X$ is triangularly distributed between $0$ and $2B$ $($with maximum at $B)$: | |
| − | $$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) | + | :$$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) |
\hspace{0.05cm},$$ $$ | \hspace{0.05cm},$$ $$ | ||
h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$ | h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$ | ||
| − | + | *Thus, for the mutual information between $X$ and $Y$: | |
| − | + | :$$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$ | |
| − | $$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$ | + | :$$\Rightarrow \hspace{0.3cm} I(X;Y) = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} |
| − | $$ = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | [[File: P_ID2890__Inf_A_4_5d.png |right|frame|Other examples of 2D PDF $f_{XY}(x, y)$]] | |
| − | + | *$I(X;Y)$ thus independent of th PDF parameters $A$ and $B$. | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
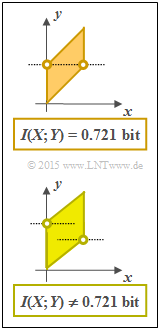
| + | '''(4)''' <u>All of the above conditions</u> are required. However, the requirements '''(2)''' and '''(3)''' are not satisfied for every parallelogram. | ||
| + | |||
| + | *The adjacent graph shows two constellations, where the random variable $X$ is equally distributed between $0$ and $1$ in each case. | ||
| + | *For the top graph, the plotted points lie at a height ⇒ $f_{Y}(y)$ is triangularly distributed ⇒ $I(X;Y) = 0.721$ bit. | ||
| + | *The lower composite PDF has a different mutual information, since the two plotted points are not at the same height <br>⇒ the PDF $f_{Y}(y)$ here has a trapezoidal shape. | ||
| + | *Feeling, I guess $I(X;Y) < 0.721$ bit, since the two-dimensional area is more approaching a rectangle. If you still feel like it, so check this statement. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.2 AWGN and Value-Continuous Input^]] |
Latest revision as of 09:27, 11 October 2021
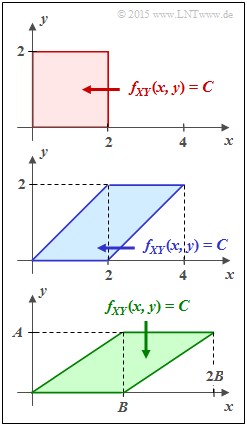
Given here are the three different two-dimensional regions $f_{XY}(x, y)$, which in the task are identified by their fill colors with
- red joint PDF,
- blue joint PDF,
- green joint PDF,
respectively. Within each of the regions shown, let $f_{XY}(x, y) = C = \rm const.$
For example, the mutual information between the continuous random variables $X$ and $Y$ can be calculated as follows:
- $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$
For the differential entropies used here, the following equations apply:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},$$
- $$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$
- $$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[ f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- For the two marginal probability density functions, the following holds:
- $$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$
- $$f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter Mutual information with continuous input.
- Let the following differential entropies also be given:
- If $X$ is triangularly distributed between $x_{\rm min}$ and $x_{\rm max}$, then:
- $$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$
- If $Y$ is equally distributed between $y_{\rm min}$ and $y_{\rm max}$, then holds:
- $$h(Y) = {\rm log} \hspace{0.1cm} \big [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}\big ]\hspace{0.05cm}.$$
- All results should be expressed in "bit". This is achieved with $\log$ ⇒ $\log_2$.
Questions
Solution
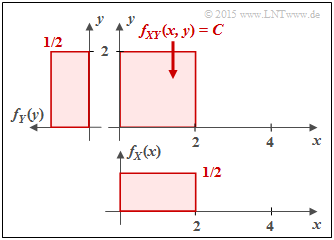
(1) For the rectangular two-dimensional PDF $f_{XY}(x, y)$ there are no statistical dependences between $X$ and $Y$ ⇒ $\underline{I(X;Y) = 0}$.
Formally, this result can be proved with the following equation:
- $$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$
- The red area of the two-dimensional PDF $f_{XY}(x, y)$ is $F = 4$.
- Since $f_{XY}(x, y)$ is constant in this area and the volume under $f_{XY}(x, y)$ must be equal to $1$, the height is $C = 1/F = 1/4$.
- From this follows for the differential joint entropy in "bit":
- $$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$
- $$\Rightarrow \hspace{0.3cm} h(XY) \ = \ \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$
- It is considered that the double integral is equal to $1$ . The pseudo-unit "bit" corresponds to the "binary logarithm" ⇒ "log2".
Furthermore:
- The marginal probability density functions $f_{X}(x)$ and $f_{Y}(y)$ are rectangular ⇒ uniform distribution between $0$ and $2$:
- $$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$
- Substituting these results into the above equation, we obtain:
- $$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} \hspace{0.05cm}.$$
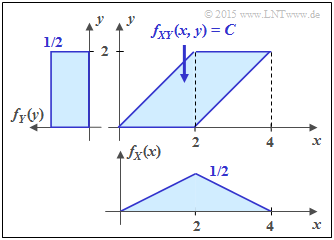
(2) Also for this parallelogram we get $F = 4, \ C = 1/4$ as well as $h(XY) = 2$ bit.
- Here, as in subtask (1) , the variable $Y$ is uniformly distributed between $0$ and $2$ ⇒ $h(Y) = 1$ bit.
- In contrast, $X$ is triangularly distributed between $0$ and $4$ $($with maximum at $2)$.
- This results in the same differential entropy $h(Y)$ as for a symmetric triangular distribution in the range between $±2$ (see specification sheet):
- $$h(X) = {\rm log}_2 \hspace{0.1cm} \big[\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}\big ] = 1.721 \,{\rm bit}$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} \hspace{0.05cm}.$$
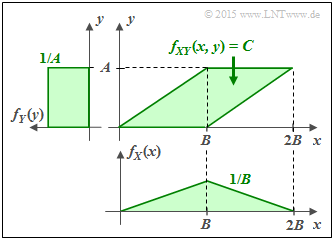
(3) The following properties are obtained for the green conditions:
- $$F = A \cdot B \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \frac{1}{A \cdot B} \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) \hspace{0.05cm}.$$
- The random variable $Y$ is now uniformly distributed between $0$ and $A$ and the random variable $X$ is triangularly distributed between $0$ and $2B$ $($with maximum at $B)$:
- $$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) \hspace{0.05cm},$$ $$ h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$
- Thus, for the mutual information between $X$ and $Y$:
- $$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} \hspace{0.05cm}.$$
- $I(X;Y)$ thus independent of th PDF parameters $A$ and $B$.
(4) All of the above conditions are required. However, the requirements (2) and (3) are not satisfied for every parallelogram.
- The adjacent graph shows two constellations, where the random variable $X$ is equally distributed between $0$ and $1$ in each case.
- For the top graph, the plotted points lie at a height ⇒ $f_{Y}(y)$ is triangularly distributed ⇒ $I(X;Y) = 0.721$ bit.
- The lower composite PDF has a different mutual information, since the two plotted points are not at the same height
⇒ the PDF $f_{Y}(y)$ here has a trapezoidal shape. - Feeling, I guess $I(X;Y) < 0.721$ bit, since the two-dimensional area is more approaching a rectangle. If you still feel like it, so check this statement.